算法入门经典-第六章 例题 6-3 矩阵链乘

题目类型： 数据结构， 链表

 输入n个矩阵的维度和一些矩阵链乘的表达式，输出乘法的次数。如果乘法无法进行，输出error。假定A是m*n矩阵，B是n*p矩阵，则乘法的次数为m*n*p。如果矩阵A的列数不等于矩阵B的行数，则这两个矩阵无法进行乘法运算。例如：A是50*10的，B是10*20的，C是20*5的，则 A（BC）的乘法次数为10*20*5（BC的乘法次数）+50*10*5（A（BC）的乘法次数）=3500.

 

要求：

第一行包括一个正整数n，表示共有n个矩阵参与运算。
接下来的n行，每行包括三部分，第一部分是矩阵的名字（一个大写字母），第二部分和第三部分各是一个正整数，分别表示该矩阵的行数和列数，这三部分之间有一个空格分隔。
最后一行包括一个矩阵运算的合法字符串（只包括小括号和上述矩阵的名称）

样例输入：

 

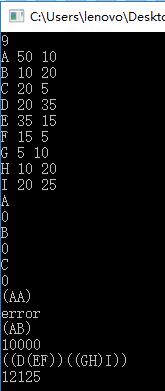
9
A 50 10
B 10 20
C 20 5
D 30 35
E 35 15
F 15 5
G 5 10
H 10 20
I 20 25
A
B
C
(AA)
(AB)
(AC)
(A(BC))
((AB)C)
(((((DE)F)G)H)I)
(D(E(F(G(HI)))))
((D(EF))((GH)I))

样例输出：

 

 

0
0
0
error
10000
error
3500
15000
40500
47500
15125

 

 

 

题目大意：

给出一系列的矩阵，给他们取名A ，B……   以及它们的行数和列数。给完后，给出一系列的表达式，然后要求求出按这些表达式进行计算，会有多少次乘法步骤。

 

解体思路：

这题和括号匹配那题很像。关键的步骤是计算矩阵乘法次数的这个过程。

 

//解析表达式 
#include<cstdio>
#include<stack>
#include<iostream>
#include<string>
using namespace std;
struct Matrix{
int a,b;
Matrix(int a=0,int b=0):a(a),b(b){
	
}
}m[26]; 
stack<Matrix> s;
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
string name;
cin>>name;
int k=name[0]-'A';
cin>>m[k].a>>m[k].b;
} 
string expr;
while(cin>>expr)
{
int len=expr.length();
bool error=false;
int ans=0;
for(int i=0;i<len;i++)
{
	if(isalpha(expr[i])) s.push(m[expr[i]-'A']);
	else if(expr[i]==')') {
		Matrix m2=s.top();
		s.pop();
		Matrix m1=s.top();
		s.pop();
		if(m1.b!=m2.a){error=true;break;
		}
		ans+=m1.a*m1.b*m2.b;
		s.push(Matrix(m1.a,m2.b));
	}
	
}
if(error) printf("error\n");
else printf("%d\n",ans);
}

return 0;
}