适合于everyone的后缀数组
后缀数组
后缀数组
$By\ $ 朝夕晨曦_L
感谢@凤年进行的排版优化
凤年の广告：后缀数组没学懂可以来学后缀自动机
小贴士
字符串前缀：从字符串开头到字符串某个位置
字符串后缀：从字符串某个位置到字符串结尾
（ 原串 和 空字符串 也是 前缀（后缀））
sa[i]：以 \(i\) 起始的后缀按字典序排序后得到的数组。表示 排名为\(i\) 的后缀的 起始位置
rk[i]：sa[i] 的映射数组，表示 起始位置为\(i\) 的后缀的 排名
sa 和 rk 可以互求，简单来说，\(sa\) 表示排名为 \(i\) 的是啥， \(rk\) 表示第 \(i\) 个的排名是啥，如果 \(sa[i] = x\),则 \(rk[x] = i\);
求\(sa|rk\)：倍增加基数排序
求SA
-
先把字符大小的信息储存到x中，初步构造出 \(sa\) 函数，这时候还不健全，仅仅按照第二关键字排序
-
开启倍增大法，先把没有后缀（不会成为别人的前缀）的扔到y的前面，后面可能会有拥有后缀的加入，并来到没有后缀的元素的后面，这就让排序更准确了（岂不是保证了从小到大？）
-
按照排名查找，如果该排名所对应的下标在k后，则可以拼接，设法将两部分拼接，从后面一段的起点找到前面一段的起点
-
重新构造 \(c\) 数组，因为上面已经用过了
-
用倒序更新 \(sa\)，用y调取到下标，下标读取到字符大小，字符大小对应排名，排名更新sa，成功进一步构造sa
-
交换 \(x\) ，\(y\)，构造全新的\(x\)，y作为之前的x还可以重复利用，重新给x标号，这次不需要用字符大小了，直接用排名大小来代替，接下来用排名大小来表示字符大小（排名小的字符小）。拼接后，只看二元组（前半部分开头排名和后半部分开头排名），二元组一样，就给他们标上同样的排名（尽管他们可能会在接下来的排名中分个高下，但现在是一个地位的）。
-
如果统计出来的排名最大值，也就是最终一共有多少个不同的二元组，二元组种类等于 \(n\) ，说明所有后缀都已经分出高下，\(sa\) 数组构造完毕，直接跳出倍增大法，如果不够，继续跑，更新最大值（m会变化，毕竟每次都枚举 \(122\) ，心疼复杂度）
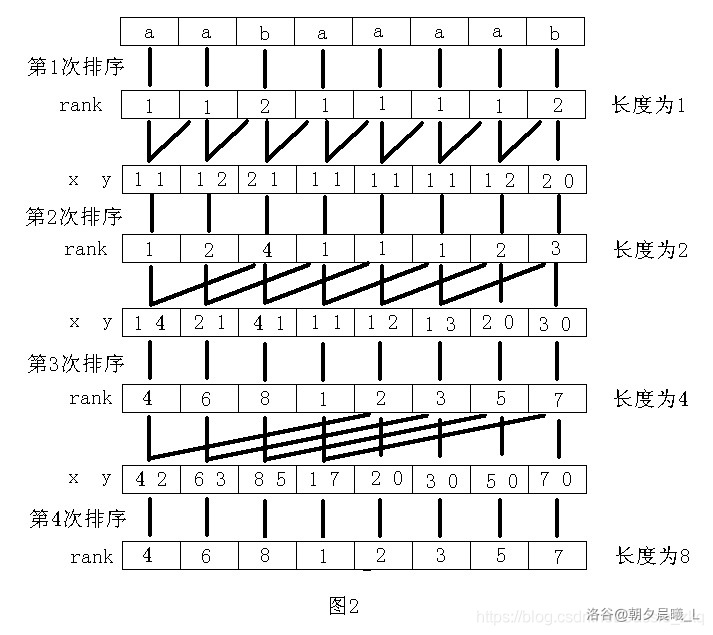
（图片来自于网络）
LCP
\(LCP(i,j)\) 为 \(suffix(sa[i])\) 与 \(suffix(sa[j])\) 的最长公共前缀
性质1: \(LCP(i,j)=LCP(j,i)\)
很显然吧。
性质2: \(LCP(i,i)=len(sa[i])=n-sa[i]+1\)
这还用证?，自己意会手推一下
有什么用呢？
- \(i>j\)，转化成 \(i<j\)
- \(i=j\)，直接算长度
so 只需要 \(i<j\)
证明
\(LCP(i,k)=\min(LCP(i,j),LCP(j,k))\ \ \ \ \ \ \ \ \ \ (1<=i<=j<=k<=n)\)
考虑将两个字符串的LCP传递，肯定需要将就小的
\[LCP(i,k) = p = \min(LCP(i,j),LCP(j,k))
\]
将区间拆分为
\[[i, i+1] 以及 [i+1, k]
\]
那么则有
\[LCP(i,k) = \min(LCP(i,i+1),LCP(i+1,k))
\]
我们可以把\([i+1, k]\)拆分，最后得出结论：
\[LCP(i,k)=min(LCP(i,j),LCP(j,k))\ \ \ \ \ \ \ \ \ \ (1<=i<=j<=k<=n)
\]
求法
\(FBI\ \ Warning:前方内容略微鬼畜，请仔细阅读！！！\)
我们设 \(height[i]\) 为 \(LCP(i,i-1)\ \ (1<i<=n)\)，特殊的，\(height[1] = 0\) (排名第0的字符串不存在)
那么\(height\)怎么求？我们可以用一个递推式
设\(h_i=height_{rk[i]}\) 则有 \(height_i=h_{sa[i]}\)（根据 \(rk\) 和 \(sa\) 的关系）
敲黑板：
\(h[i]\geq h[i-1]-1\)
请务必看懂证明，因为做题都与h数组和height数组的性质有关
规定第\(i-1\)个字符串按排名来的前面的那个字符串是第 \(k\) 个字符串，\(k\) 的下标不（一定）是 \(i-2\)，而是\(rk[k]=rk[i-1]-1\)
由\(height\)的定义可得：第 \(k\) 个字符串和第 \(i-1\) 个字符串的公共前缀是 \(height_{rk[i-1]}\)（这不就是定义？）
我们只需要思考第 \(k+1\) 个字符串和第 \(i\) 个字符串的关系。
- \(Case 1: 第 k 个字符串和第 i-1 个字符串的首字符不同\) *
知道整个串的大小排名，而且第一个字符的大小不一样大，那么两个串第一个字符谁大谁小易知，可是你得到了这个信息，却失去了剩下字符串谁大谁小的信息，无法保证两个串中第二个字符谁大谁小，也就不知道第 \(k+1\) 个和第 \(i\) 个字符的排名大小
也就是说第 \(k+1\) 个字符串的排名既可能在 \(i\) 的前面，也可能在 \(i\) 的后面
But，换个思路，第 \(k\) 个和第 \(i-1\) 个字符不同，那么 \(height_{rk[i-1]}\) 就是 \(0\) 了，那么无论 \(height_{rk[i]}\) 是多少都会有 \(height_{rk[i]}\geq height_{rk[i-1]}-1\) ，也就是 \(h[i] \geq h[i-1]-1\)。（显然正确）
- \(Case 2: 第 k 个字符串和第 i-1 个字符串的首字符相同\) *
由于第 \(k+1\) 个字符串是第 \(k\) 个字符串 去掉首字符 得到的，第 \(i\) 个字符串是第 \(i-1\) 个字符串 去掉首字符 得到的，那么第k+1个字符串 一定 排在第 \(i\) 个字符串前面（上次对于 \(i-1\) 和 \(k\) 的比较已经得到该结果），已知第 \(k\) 个字符串和第 \(i-1\) 个字符串的最长公共前缀是 \(height_{rk[i-1]}\)，那么自然第 \(k+1\) 个字符串和第 \(i\) 个字符串的最长公共前缀就是 \(height_{rk[i-1]}-1\)。（掐去开头）
远远么有结束：
对于比第 \(i\) 个字符串的排名更靠前的那些字符串，谁和第 \(i\) 个字符串长得最像？显然是排名紧邻第 \(i\) 个字符串的那个字符串了呀，即 \(suffix(sa[rk[i]-1])\) 。但是我们前面求得，有一个一定排在 \(i\) 前面的字符串 \(k+1\) ，\(LCP(rk[i],rk[k+1])=height[rk[i-1]]-1\);
因为第 \(k+1\) 个可能不是长得最像的
\[height[rk[i]]=LCP(rk[i], rk[i]-1)\geq LCP(rk[i], rk[k+1])
\]
那么把式子汇总
\[height[rk[i]]=LCP(rk[i],rk[i]-1) \geq LCP(rk[i],rk[k+1]) = height[rk[i-1]]-1
\]
从 \(i\) 引到 \(i-1\)（下标的前一个） 再从 \(i-1\) 引到 \(k\)（排名的前一个） 从 \(k\)引到 $k+1 $（下标的下一位）的同时从 \(i-1\) 引到 \(i\)（下标的下一位），利用 \(i\) 和 \(k+1\)（不一定最相似的两个）的关系，列出不等式，就找到了 \(i\) 和 \(i-1\)（下标的前一位）的关系（这里的字母都表示下标）
得到 $$height[rk[i]] \geq height[rk[i-1]]-1$$ ，即 $$h[i] \geq h[i-1]-1$$ 。
（h数组的迭代方式实现从排名转到下标）
代码
Code
string s;
int n /*长度*/, m = 122 /*字符集*/;
int y[M], x[M], c[M], sa[M], rk[M], height[M];
void get_sa() { // （从小到大排序）
for(int i = 1; i <= n; ++i) // 下标
++c[x[i] = s[i]]; // 统计该大小元素的个数
for(int i = 2; i <= m; ++i) // 大小
c[i] += c[i - 1]; // 塑造排名
for(int i = n; i >= 1; --i) // 下标
sa[c[x[i]]--] = i; // 排队，倒序拍更稳定，将相同大小的按照输入顺序储存
// x是第一关键字
for(int k = 1; k <= n; k <<= 1) { // 倍增
int num = 0;
// 构造y数组，y[第二关键字排名]=第一关键字的位置
for(int i = n - k + 1; i <= n; ++i) // 下标
y[++num] = i;
// y数组此时成功储存k后部分
// 之前的排名定命运，已经初步排名，有着相同前缀的两个串
// 没有后缀一定小于有后缀的，那么就按照前缀大小
// 从小到大的顺序把这些前缀放在前面，因为他们相对会小（后补0）
for(int i = 1; i <= n; ++i) // 排名
if(sa[i] > k) y[++num] = sa[i] - k;
//y数组k前入库，y数组完整啦
// 用下标在后的找到下标在前的，sa[i]>k保证有前导，
// sa[i]-k就是拼接起来的第一个字符的下标
for(int i = 1; i <= m; ++i) // 大小
c[i] = 0;
for(int i = 1; i <= n; ++i) // 下标
++c[x[i]];
// 重新构造一下，之前的c数组归位了
for(int i = 2; i <= m; ++i) // 大小
c[i] += c[i - 1];
for(int i = n; i >= 1; --i) // 排名
sa[c[x[y[i]]]--] = y[i], y[i] = 0;
// x套y 用y调取下标，用下标调取字符大小，
// 用字符大小调取排名，用排名调取下标，重复利用x
// 排名为（排名为i的字符所对应的第一关键字下标的字符大小所对应的排名 ）的串的下标 就是 第一关键字的下标
// 宏观上来看，第二关键字排好了，现在排第一关键字，在第二关键字排好的基础上，根据第一关键字的大小排序
// 并且这个过程并不打乱第二关键字的顺序（倒序）
swap(x, y); // 现在的y是之前的x，所以现在y储存的是字符大小（通过下标找到字符大小）
x[sa[1]] = 1; // 排名为1的下标对应的的字符大小为1
num = 1; // 排序，重复的共用一个排名
for(int i = 2; i <= n; ++i) { /*排名*/
if(y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) { // 拼接的两部分完全相同
x[sa[i]] = num; // 共用一个排名，排名也可以用来做大小，压缩m的大小，优化
} else {
x[sa[i]] = ++num; // 开辟新排名
}
}
if(num == n) break; // 排名延伸到n，那么排名与下标一一对应，收工
m = num; // 更新一下最大值
}
}
void get_lcp() {
int k = 0; // 初始化
for(int i = 1; i <= n; ++i) rk[sa[i]] = i; // 构造映射数组
for(int i = 1; i <= n; ++i) { // 下标
if(rk[i] == 1) continue; // 排名第一的height为0
if(k) --k; // h[i]数组的传递
int j = sa[rk[i] - 1]; // 排名在i前一个的串下标
while(j + k <= n && i + k <= n /*没越界*/ && s[i + k] == s[j + k] /*扩展lcp*/) ++k;
height[rk[i]] = k; // 储存
}
}
int main() {
scanf("%d", &n);
cin >> s;
s = '0' + s; // 下标从1开始
get_sa();
get_lcp();
...
return 0;
}
应用
没错这就是一道连 \(LCP\) 都用不到的紫色板子题蓝色板子题
这是 @凤年 找到的例题，大家可能会想，后缀数组不是处理字符串的？
有没有一种可能？处理字符串也是把字符串转成数字？
那么开始抄家伙！
把第一个加到末尾？那我们直接把整个串 \(copy\) 到后面，在根据调取的起点不同，实现不同状态的区分不就好了？需要注意的是要判一下越界，再者是需要注意数字可能为 \(0\) ！！！
int cnt = 1;
while(sa[cnt] + (n / 2) > n) cnt++; // 找到第一个不越界的串，也就是最小的
for(int i = 0; i <= (n / 2) - 1; ++i) cout << p[sa[cnt] + i] << " "; // 输出这个串
代码：
Code
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <string>
#define M 1000050
using namespace std;
int n, m, l;
int p[M], y[M], x[M], c[M], sa[M], rk[M], height[M];
void get_sa() {
for(int i = 1; i <= n; ++i) ++c[x[i]];
for(int i = 1; i <= m; ++i) c[i] += c[i - 1];
for(int i = n; i >= 1; --i) sa[c[x[i]]--] = i;
for(int k = 1; k <= n; k <<= 1) {
int num = 0;
for(int i = n - k + 1; i <= n; ++i) y[++num] = i;
for(int i = 1; i <= n; ++i)
if(sa[i] > k) y[++num] = sa[i] - k;
for(int i = 0; i <= m; ++i) c[i] = 0;
for(int i = 1; i <= n; ++i) ++c[x[i]];
for(int i = 1; i <= m; ++i) c[i] += c[i - 1];
for(int i = n; i >= 1; --i) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1;
num = 1;
for(int i = 2; i <= n; ++i) {
if(y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) {
x[sa[i]] = num;
} else {
x[sa[i]] = ++num;
}
}
if(num == n) break;
m = num;
}
int cnt = 1;
while(sa[cnt] + (n / 2) > n) {
cnt++;
}
for(int i = 0; i <= (n / 2) - 1; ++i) cout << p[sa[cnt] + i] << " ";
}
int main() {
cin >> n;
for(int i = 1, w; i <= n; i++) {
cin >> w;
m = max(m, w);
x[i] = w;
p[i] = w;
p[i + n] = p[i];
x[i + n] = x[i];
}
n = n + n;
get_sa();
return 0;
}
啧啧啧，这题咋嫩眼熟？这波直接判断一下不越界然后输出最后一个字符即可（注意是小于等于 \(n-1\) ，小于等于 \(n\) 会和原串重复）
Code
#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
#include<cmath>
#define M 1000050
using namespace std;
string s;
int n /*长度*/, m = 122 /*字符集*/, l ;
int y[M], x[M], c[M], sa[M], rk[M], height[M];
void get_sa() {
for(int i = 1; i <= n; ++i)
++c[x[i] = s[i]];
for(int i = 2; i <= m; ++i)
c[i] += c[i - 1];
for(int i = n; i >= 1; --i)
sa[c[x[i]]--] = i;
for(int k = 1; k <= n; k <<= 1) {
int num = 0;
for(int i = n - k + 1; i <= n; ++i)
y[++num] = i;
for(int i = 1; i <= n; ++i)
if(sa[i] > k) y[++num] = sa[i] - k;
for(int i = 1; i <= m; ++i)
c[i] = 0;
for(int i = 1; i <= n; ++i)
++c[x[i]];
for(int i = 2; i <= m; ++i)
c[i] += c[i - 1];
for(int i = n; i >= 1; --i)
sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1;
num = 1;
for(int i = 2; i <= n; ++i) {
if(y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) {
x[sa[i]] = num;
} else {
x[sa[i]] = ++num;
}
}
if(num == n) break;
m = num;
}
for(int i = 1;i <= l * 2; ++i) if(sa[i] + l - 1 < l * 2) cout << s[sa[i] + l -1];
}
void get_lcp() {
int k = 0;
for(int i = 1; i <= n; ++i) rk[sa[i]] = i;
for(int i = 1; i <= n; ++i) {
if(rk[i] == 1) continue;
if(k) --k;
int j = sa[rk[i] - 1];
while(j + k <= n && i + k <= n /*没越界*/ && s[i + k] == s[j + k] /*扩展lcp*/) ++k;
height[rk[i]] = k;
}
}
int main() {
cin >> s;
l = s.size();
s = '0' + s + s;
n = l * 2;
get_sa();
// get_lcp();
return 0;
}
题目要求求出在字典序最小的新序列，考虑如何保证字典序最小。
首先当前局面，我们肯定会选择两个序列中字典序较小的那个元素放进新序列。
但是万一两个序列队首元素字典序相同呢？那么我们就要有预知能力。
而后缀排序就赋予我们预知能力，我们把其中一个序列看做主序列，在接下来有来自次序列的元素插入，打乱了主序列，这会不会影响答案正确性？当前选择排名较小的会不会错误？
显然不会，因为这因为排名小实际上是预知了接下来谁会更早的解救出字典序小的元素，当前局面选谁都一样，就要考虑选了谁，能快速获得字典序小的元素，这样就完美解决了这个问题。
Code
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 400050
char buf[1<<21],*p1,*p2;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
long long read(){
long long res=0,f=1;char ch;
for(ch=getchar();ch<'0'||ch>'9';ch=getchar())
if(ch=='-') f=-1;
for(;ch>='0'&&ch<='19';ch=getchar())
res=(res<<3)+(res<<1)+ch-'0';
return res*f;
}
void wt(int x){
if(x<0) return putchar('-'),wt(-x);
if(x>=10) wt(x/10);
putchar(x%10+'0');
return ;
}
int wa[N],wb[N],s[N],la,lb;
int a[N],b[N];
int n, m = 1001, l, t, p;
int y[N], x[N], c[N], sa[N], rk[N], height[N];
void get_sa() {
for(int i = 1; i <= n; ++i) ++c[x[i] = s[i]];
for(int i = 2; i <= m; ++i) c[i] += c[i - 1];
for(int i = n; i >= 1; --i) sa[c[x[i]]--] = i;
for(int k = 1; k <= n; k <<= 1) {
int num = 0;
for(int i = n - k + 1; i <= n; ++i) y[++num] = i;
for(int i = 1; i <= n; ++i)
if(sa[i] > k) y[++num] = sa[i] - k;
for(int i = 1; i <= m; ++i) c[i] = 0;
for(int i = 1; i <= n; ++i) ++c[x[i]];
for(int i = 2; i <= m; ++i) c[i] += c[i - 1];
for(int i = n; i >= 1; --i) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1;
num = 1;
for(int i = 2; i <= n; ++i) {
if(y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k])
x[sa[i]] = num;
else
x[sa[i]] = ++num;
}
if(num == n) break;
m = num;
}
}
int main(){
la=read();
int i;
for(i=1;i<=la;i++){
a[i]=read();
s[++n]=a[i];
}
lb=read();
s[++n]=1001;//有一个用完，只能用另外一个，所以只好给个极大值
for(i=1;i<=lb;i++){
b[i]=read();
s[++n]=b[i];
}
// for(int i=1;i<=n;i++){
// cout<<s[i]<<" ";
// }
// cout<<endl;
get_sa();
for(int i=1;i<=n;i++){
rk[sa[i]]=i;
}
int j=1,k=la+2;
while(j<=la&&k<=n){
if(rk[j]<rk[k]) wt(s[j++]),printf(" ");
else wt(s[k++]),printf(" ");
}
while(j<=la) wt(s[j++]),printf(" ");
while(k<=n) wt(s[k++]),printf(" ");
return 0;
}
以上都没有用到LCP，那么我们学的LCP咋用？
考虑一共会产生多少的子串？以第一个字符为起点，有n个串······以第n个字符为起点，有1个
根据首项+末项）*项数/2
得到（n+1）*n/2（记得开long long）
那么接下来怎样删去重复的子串，就用height！删去所有height即可！
\[\frac{n\times(n + 1)}{2}-{\sum\limits_{i = 1}^{n}{height[i]}}
\]
怎么推出来的？
考虑我们将排好序的后缀对好位置写出来，每次新的贡献是
\[[sa[i],sa[i] + height[i] + 1],[sa[i],sa[i] + height[i] + 2]······[sa[i],n]
\]
相当于在所有的串里剖去了 \(1\) ~ \(height_i\)的部分，在总串数里减去即可！
long long solve (){
long long ans = ((long long)n * (long long)(n+1)) / 2;
for(int i = 1;i <= n; ++ i) ans -= height[rk[i]];
return ans;
}
SUBST1 - New Distinct Substrings
双倍经验
首先揣摩一番，真不错 \(62.5 MB\) 内存，出题人真是丧心病狂心思细腻啊。让我来猜猜他想卡掉什么？首先排除SAM（确信）
仔细一想，出题人远远没有你想象的那么当人简单，它不仅卡掉了SAM,他甚至不让你用 ST表！
多个串求后缀数组，一个一个建立显然不现实（超时大礼包），那么我们就全部拼接在一起，来一个大锅菜。
那么，前面偷懒了，统计答案可就没那么好过了。
我们遍历整个后缀数组，对于任意两串的最长公共前缀，我们必须要取目前遍历到的 \(height\) 数组最小值；对于每次遍历到一个串的某个字符，要给当前串的最小长度数组重新赋极大值，因为接下来的操作与前一个该串元素所构成的后缀无关，只与新遍历到的该串元素构成的后缀有关；对于每两个串之间产生的答案，我们统一取最大值。
这样思路就了然了，见代码：
Code
#include "bits/stdc++.h"
using namespace std;
const int N = 1e6 + 55 , Inf = 1e9;
int height[N],y[N],rk[N],sa[N],cnt[N],x[N],odrk[N],p,ID[N],lst[N],Minn[55],Ans[55][55];
int n,m;
char s[N],ss[N];
bool cmp(int x,int y,int w){
return odrk[x] == odrk[y] && odrk[x + w] == odrk[y + w];
}
int main(){
int x = 1;
int T;
scanf("%d",&T);
for(int j = 1 ; j <= T ; j ++){
scanf("%s",ss + 1);
int lenss = strlen(ss + 1);
for(int i = 1 ; i <= lenss ; i ++){
s[++ n] = ss[i];//拼接
ID[n] = j;
}
while('a' <= x && x <= 'z') x++;
s[++ n] = char(x);
x ++;//插入无关字符
}
//sa
m = max(300 , n);
for(int i = 1 ; i <= n ; i ++) ++ cnt[rk[i] = s[i]];
for(int i = 1 ; i <= m ; i ++) cnt[i] += cnt[i - 1];
for(int i = n ; i >= 1 ; i --) sa[cnt[rk[i]] --] = i;
for(int w = 1 ; ; w <<= 1 , m = p){
p = 0;
for(int i = n ; i > n - w ; i --) y[++ p] = i;
for(int i = 1 ; i <= n ; i ++) if(sa[i] > w) y[++ p] = sa[i] - w;
memset(cnt , 0 , sizeof cnt);
for(int i = 1 ; i <= n ; i ++) ++ cnt[x[i] = rk[y[i]]];
for(int i = 1 ; i <= m ; i ++) cnt[i] += cnt[i - 1];
for(int i = n ; i >= 1 ; i --) sa[cnt[x[i]] --] = y[i];
memcpy(odrk , rk , sizeof(rk));
p = 0;
for(int i = 1 ; i <= n ; i ++) rk[sa[i]] = cmp(sa[i - 1] , sa[i] , w) ? p : ++ p;
if(p == n){
for(int i = 1 ; i <= n ; i ++) rk[sa[i]] = i;
break;
}
}
//lcp
for(int i = 1 , len = 0 ; i <= n ; i ++){
if(rk[i] == 1) continue;
if(len) len --;
while(s[i + len] == s[sa[rk[i] - 1] + len]) len ++;
height[rk[i]] = len;
}
for(int i = 1 ; i <= T ; i ++) {
Minn[i] = Inf;
for(int j = 1 ; j <= T ; j ++) Ans[i][j] = 0;
}//初始化
for(int i = 1 ; i <= n ; i ++){//排名
int irui = ID[sa[i]];//查询处于哪个串
if(irui){//不是无关字符
for(int j = 1 ; j <= T ; j ++){
Minn[j] = min(Minn[j] , height[i]);
if(Minn[j] == Inf || irui == j) continue;
Ans[irui][j] = max(Ans[irui][j] , Minn[j]);
Ans[j][irui] = Ans[irui][j];//双向
}
Minn[irui] = Inf;//出现一个就可以更新
}
}
for(int i = 1 ; i <= T ; i ++){
for(int j = 1 ; j <= T ; j ++)
if(i != j) printf("%d ",Ans[i][j]);
puts("");
}
return 0;
}
这是一道好题！！！
大家需要非常充分的了解后缀数组，在思维与应用上是一个很大的提高
另外还有充分理解子串的概念，懂得子串的大小关系
最后还需要输出的艺术
它有两个分支： t=0 , t=1
(博主懒得给你解释了，自己看去吧)
博主又回来了
把排好序的后缀纵向排列
\(针对一样的串算一个\)
侧重于横向查找，重叠部分直接过滤
\(针对一样的串算多个\)
侧重于纵向查找，重叠部分一一计数
详解见代码
Code
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <string>
using namespace std;
const int M = 1000050;
int n, m, l, t, p;
string s;
int y[M], x[M], c[M], sa[M], rk[M], height[M];
void get_sa() {
for(int i = 1; i <= n; ++i) ++c[x[i] = s[i]];
for(int i = 2; i <= m; ++i) c[i] += c[i - 1];
for(int i = n; i >= 1; --i) sa[c[x[i]]--] = i;
for(int k = 1; k <= n; k <<= 1) {
int num = 0;
for(int i = n - k + 1; i <= n; ++i) y[++num] = i;
for(int i = 1; i <= n; ++i)
if(sa[i] > k) y[++num] = sa[i] - k;
for(int i = 1; i <= m; ++i) c[i] = 0;
for(int i = 1; i <= n; ++i) ++c[x[i]];
for(int i = 2; i <= m; ++i) c[i] += c[i - 1];
for(int i = n; i >= 1; --i) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1;
num = 1;
for(int i = 2; i <= n; ++i) {
if(y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k])
x[sa[i]] = num;
else
x[sa[i]] = ++num;
}
if(num == n) break;
m = num;
}
}
void get_lcp() {
int k = 0;
for(int i = 1; i <= n; ++i) rk[sa[i]] = i;
for(int i = 1; i <= n; ++i) {
if(rk[i] == 1) continue;
if(k) --k;
int j = sa[rk[i] - 1];
while(j + k <= n && i + k <= n && s[i + k] == s[j + k]) ++k;
height[rk[i]] = k;
}
}
int main() {
cin >> s;
s = '0' + s;
n = s.size() - 1;
m = 122;
get_sa();
get_lcp();
scanf("%d%d", &t, &p);
//我们现在手里捏着p，想要用小的去填补，一步步消去p，直到找到第p位
//第p位一定会出现在这次能抵消的数量大于等于p时
if(t == 0) {//相同的串算一个
for(int i = 1; i <= n; i++) {//枚举每一个串
if(n - sa[i] + 1 - height[i] < p) // 剖去这次的贡献
p -= n - sa[i] + 1 - height[i];
//这次的贡献是这个串的长度减去与上面重叠的长度
//因为这个长度上面已经记录了，相同的串算一个！
else {//显然，答案诞生了！
for(int j = 0; j <= height[i] + p - 1; j++)
// 第p大的一定诞生在这个串里，只需要考虑输出前p个字符
printf("%c", s[sa[i] + j]);
return 0;
}
}
printf("-1");
}
//关于为什么前p个字符构成的串是第p位
//因为整体上已经排好序了，相当于分开了几个区间
//并且在一个区间内，也是有序的，毕竟多一个字符就变大了
//so 前p位构成的串在这整个串里排名第p
if(t == 1) {//这次长得一样的需要重复统计
for(int i = 1; i <= n; i++) {//从小到大枚举串
for(int k = height[i] + 1; k <= n - sa[i] + 1; k++) {
//前面的长度不可以重复使用了，直接继承height[i]
//从height[i]+1开始枚举
if(p > 1) p --;//剖去1，这次只剖去一个
//等一下纵向遍历接着剖
else {//承受不住了，第一波就没了
for(int t = sa[i]; t <= sa[i] + k - 1; t++)
cout << s[t];
//直接输出
//输出是一门艺术
//我们枚举的就是k（长度），输出的话就方便了许多
//找到起点，正是sa[i]
return 0;
}
for(int j = i + 1; j <= n; j++) {
if(k <= height[j]) {//这个串能够承受这个长度
//当前大小的串，要满足长得一模一样
//那么纵向就要满足k <= height[j]
if(p > 1) p --;//接着消
else {
for(int t = sa[i]; t <= sa[i] + k - 1; t++)//输出，玩挺花
cout << s[t];
return 0;
}
}
else break;//没有该大小的串了，没必要接着消了
}
}
}
printf("-1");//遍历了所有的串，都没p大，那就说明你给的p超标了！
//输出-1
}
return 0;
}
LCS - Longest Common Substring
只需要判断是否分布在两个串里，然后统计答案
Code
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <string>
using namespace std;
const int M = 1000050;
string s,ss;
int n /*长度*/, m = 122 /*字符集*/;
int y[M], x[M], c[M], sa[M], rk[M], height[M], maxn, siz;
void get_sa() { // （从小到大排序）
for(int i = 1; i <= n; ++i) // 下标
++c[x[i] = s[i]]; // 统计该大小元素的个数
for(int i = 2; i <= m; ++i) // 大小
c[i] += c[i - 1]; // 塑造排名
for(int i = n; i >= 1; --i) // 下标
sa[c[x[i]]--] = i; // 排队，倒序拍更稳定，将相同大小的按照输入顺序储存
// x是第一关键字
for(int k = 1; k <= n; k <<= 1) { // 倍增
int num = 0;
// 构造y数组，y[第二关键字排名]=第一关键字的位置
for(int i = n - k + 1; i <= n; ++i) // 下标
y[++num] = i;
// 之前的排名定命运，已经初步排名，有着相同前缀的两个串
// 没有后缀一定小于有后缀的，那么就按照前缀大小
// 从小到大的顺序把这些前缀放在前面，因为他们相对会小（后补0）
for(int i = 1; i <= n; ++i) // 排名
if(sa[i] > k) y[++num] = sa[i] - k;
// 用下标在后的找到下标在前的，sa[i]>k保证有前导，
// sa[i]-k就是拼接起来的第一个字符的下标
for(int i = 1; i <= m; ++i) // 大小
c[i] = 0;
for(int i = 1; i <= n; ++i) // 下标
++c[x[i]];
// 重新构造一下，之前的c数组归位了
for(int i = 2; i <= m; ++i) // 大小
c[i] += c[i - 1];
for(int i = n; i >= 1; --i) // 排名
sa[c[x[y[i]]]--] = y[i], y[i] = 0;
// x套y 用y调取下标，用下标调取字符大小，
// 用字符大小调取排名，用排名调取下标，重复利用x
// 排名为（排名为i的字符所对应的第一关键字下标的字符大小所对应的排名 ）的串的下标 就是 第一关键字的下标
// 宏观上来看，第二关键字排好了，现在排第一关键字，在第二关键字排好的基础上，根据第一关键字的大小排序
// 并且这个过程并不打乱第二关键字的顺序（倒序）
swap(x, y); // 现在的y是之前的x，所以现在y储存的是字符大小（通过下标找到字符大小）
x[sa[1]] = 1; // 排名为1的下标对应的的字符大小为1
num = 1; // 排序，重复的共用一个排名
for(int i = 2; i <= n; ++i) {/*排名*/
if(y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) { // 拼接的两部分完全相同
x[sa[i]] = num; // 共用一个排名，排名也可以用来做大小，压缩m的大小，优化
} else {
x[sa[i]] = ++num; // 开辟新排名
}
}
if(num == n) break; // 排名延伸到n，那么排名与下标一一对应，收工
m = num; // 更新一下最大值
}
}
void get_lcp() {
int k = 0; // 初始化
for(int i = 1; i <= n; ++i) rk[sa[i]] = i; // 构造映射数组
for(int i = 1; i <= n; ++i) { // 下标
if(rk[i] == 1) continue; // 排名第一的height为0
if(k) --k; // h[i]数组的传递
int j = sa[rk[i] - 1]; // 排名在i前一个的串下标
while(j + k <= n && i + k <= n /*没越界*/ && s[i + k] == s[j + k] /*扩展lcp*/) ++k;
height[rk[i]] = k; // 储存
}
}
void solve(){
for(int i = 2;i <= n;i++){
if(maxn < height[i]){
if((sa[i] > siz) && (sa[i-1] < siz) || (sa[i] < siz) && (sa[i-1] > siz)){
maxn = height[i];
}
}
}
printf("%d",maxn);
}
int main() {
cin >> s;cin >> ss;
siz = s.size() + 1;
s = '0' + s + 'A' + ss; // 下标从1开始
n = s.size() - 1;
get_sa();
get_lcp();
solve();
return 0;
}
多个串就不可以瞎搞了，我们可以选择老老实实模拟，看看是不是符合每个串都可以达到这个长度的相同串
怎么处理串？将所有串拼接，中间插入一个无关串
怎样判断属于第几个串？开个数组指向区间编号
怎么判断能否达到该长度？开二维 \(bool\) 数组，第一维存串编号，第二维存长度
怎么维护bool数组？
\(height\) 不变正常处理
\(height\) 变大了先统计答案（别忘了），再把（height[i-1],height[i] ]清零
\(height\) 变小了先统计答案（别忘了），再把（height[i],height[i-1] ]清零
这是拿下这题的关键
Code
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <string>
using namespace std;
const int M = 1000050;
/*
2
bbabbbbbab
abaabbaabb
2
ababb
aaaaa
*/
string s, ss;
int n /*长度*/, m = 126 /*字符集*/;
int y[M], x[M], c[M], sa[M], rk[M], height[M], maxn, siz;
int go[1000001];
bool ye[11][M];
int cnt = 0;
void get_sa() {
for(int i = 1; i <= n; ++i) ++c[x[i] = s[i]];
for(int i = 2; i <= m; ++i) c[i] += c[i - 1];
for(int i = n; i >= 1; --i) sa[c[x[i]]--] = i;
for(int k = 1; k <= n; k <<= 1) {
int num = 0;
// for(int i=1;i<=num;i++) numm[i]=0;
for(int i = n - k + 1; i <= n; ++i) y[++num] = i;
for(int i = 1; i <= n; ++i)
if(sa[i] > k) y[++num] = sa[i] - k;
for(int i = 1; i <= m; ++i) c[i] = 0;
for(int i = 1; i <= n; ++i) ++c[x[i]];
for(int i = 2; i <= m; ++i) c[i] += c[i - 1];
for(int i = n; i >= 1; --i) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1;
num = 1;
for(int i = 2; i <= n; ++i) {
if(y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) {
x[sa[i]] = num;
// ++numm[num];
} else {
x[sa[i]] = ++num;
}
}
if(num == n) break;
m = num;
}
}
void get_lcp() {
int k = 0;
for(int i = 1; i <= n; ++i) rk[sa[i]] = i;
for(int i = 1; i <= n; ++i) {
if(rk[i] == 1) continue;
if(k) --k;
int j = sa[rk[i] - 1];
while(j + k <= n && i + k <= n && s[i + k] == s[j + k] && s[i + k] != '~') ++k;
height[rk[i]] = k;
}
}
void solve() {
int l_max = 0;
char last = s[sa[1]];
for(int i = 2; i <= n; i++) {
if(s[sa[i]] == '~') continue;
l_max = max(l_max, height[i]);
if(s[sa[i]] != last) {
for(int j = l_max; j >= 1; --j) {
bool flag = 1;
for(int k = 1; k <= cnt; ++k) {
if(ye[k][j]) ye[k][j - 1] = 1;
if( ! ye[k][j]) flag = 0;
if(k == cnt && flag) maxn = max(maxn, j);
}
if(flag) break;
} // 更新答案
memset(ye, 0, sizeof(ye));
last = s[sa[i]];
continue;
}
if(height[i] < height[i - 1]) { // 后面不会更新到长的了，短的可以再次利用长的里面的短的
for(int j = l_max; j >= 1; --j) {
bool flag = 1;
for(int k = 1; k <= cnt; ++k) {
if(ye[k][j]) ye[k][j - 1] = 1;
if( ! ye[k][j]) flag = 0;
if(k == cnt && flag) maxn = max(maxn, j);
}
if(flag) break;
} // 更新答案
for(int j = height[i] + 1; j <= height[i - 1]; j++) {
for(int k = 1; k <= cnt; k++) {
ye[k][j] = 0; // 清空，接下来的长串不能再次利用
}
}
}
if(height[i] > height[i - 1]) {
for(int j = l_max; j >= 1; --j) {
bool flag = 1;
for(int k = 1; k <= cnt; ++k) {
if(ye[k][j]) ye[k][j - 1] = 1;
if( ! ye[k][j]) flag = 0;
if(k == cnt && flag) maxn = max(maxn, j);
}
if(flag) break;
} // 更新答案
for(int j = height[i - 1] + 1; j <= height[i]; j++) {
for(int k = 1; k <= cnt; k++) {
ye[k][j] = 0; // 清空，接下来的长串不能再次利用
}
}
}
ye[go[sa[i]]][height[i]] = 1;
ye[go[sa[i - 1]]][height[i]] = 1;
}
for(int j = l_max; j >= 1; --j) {
bool flag = 1;
for(int k = 1; k <= cnt; ++k) {
if(ye[k][j]) ye[k][j - 1] = 1;
if( ! ye[k][j]) flag = 0;
if(k == cnt && flag) maxn = max(maxn, j);
}
if(flag) break;
} // 更新答案
printf("%d", maxn);
}
int main() {
cin >> n;
s = '0';
while(cin >> ss) {
++cnt;
s += '~';
for(int i = 0; i < int(ss.size()); ++i) {
s += ss[i];
go[s.size() - 1] = cnt;
}
}
n = s.size() - 1;
get_sa();
get_lcp();
solve();
return 0;
}
计算公式。
首先我们观察一下这个式子，前面两项都是长度，是很显然的，(n − 1) ∗ n ∗ (n + 1) / 2
那么我们实际要做的，是求 \(lcp\) ( \(T_i\) , \(T_j\) )。
莫非 \(n^2\) 枚举？很明显会 T （30 pts），现在考虑如何高效统计每个区间的最小 \(height\) 值的加和
现在我们的目标是求出 \(height\) 数组里，左右两边比 \(height_i\) 小的第一个数的下标，这样我们就可以拼接区间，求和了！
Code
#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
#include<cmath>
#define M 1000050
using namespace std;
string s;
int n /*长度*/, m = 122 /*字符集*/, top;
int sta[M], y[M], x[M], L[M], R[M], c[M], sa[M], rk[M], height[M];
long long res;
void get_sa() {
for(int i = 1; i <= n; ++i)
++c[x[i] = s[i]];
for(int i = 2; i <= m; ++i)
c[i] += c[i - 1];
for(int i = n; i >= 1; --i)
sa[c[x[i]]--] = i;
for(int k = 1; k <= n; k <<= 1) {
int num = 0;
for(int i = n - k + 1; i <= n; ++i)
y[++num] = i;
for(int i = 1; i <= n; ++i)
if(sa[i] > k) y[++num] = sa[i] - k;
for(int i = 1; i <= m; ++i)
c[i] = 0;
for(int i = 1; i <= n; ++i)
++c[x[i]];
for(int i = 2; i <= m; ++i)
c[i] += c[i - 1];
for(int i = n; i >= 1; --i)
sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1;
num = 1;
for(int i = 2; i <= n; ++i) {
if(y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) {
x[sa[i]] = num;
} else {
x[sa[i]] = ++num;
}
}
if(num == n) break;
m = num;
}
}
void get_lcp() {
int k = 0;
for(int i = 1; i <= n; ++i) rk[sa[i]] = i;
for(int i = 1; i <= n; ++i) {
if(rk[i] == 1) continue;
if(k) --k;
int j = sa[rk[i] - 1];
while(j + k <= n && i + k <= n /*没越界*/ && s[i + k] == s[j + k] /*扩展lcp*/) ++k;
height[rk[i]] = k;
}
}
void solve(){
long long res = 0;
sta[ ++top] = 1;
for(int i = 2;i <= n; i++){
//用来存储每个元素左边和右边第一个比它小的元素的下标。
while(top && height[sta[top]] >= height[i]) R[sta[top --]] = i;
L[i] = sta[top];
sta[ ++top] = i;
}
while(top)R[sta[top--]] = n + 1;
for(int i = 2;i <= n;i ++)res += 1ll * height[i] * (i - L[i]) * (R[i] - i);
int n=heigh();
printf("%lld\n",1ll * (n - 1) * n * (n + 1) / 2 - 2 * res);
}
int main() {
cin >> s;
n = s.size();
s = '0' + s;
get_sa();
get_lcp();
solve();
return 0;
}
P2178 [NOI2015] 品酒大会
并查集 + 后缀数组
Code
#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
#include<cmath>
#include<vector>
#define M 1000050
using namespace std;
int n,m,l;
const long long inf=2e20;
string s,ss;
long long w[M],siz[M],fa[M];
long long max1[M],max2[M],min1[M],min2[M];//最大值次大值
int y[M],x[M],c[M],sa[M],rk[M],height[M],maxn=0;
long long ans[M][2];
//ans[r][0] 表示选出两杯 r 相似酒调兑的方法数
//ans[r][1] 表示选出两杯 r 相似酒调兑的美味度的最大值
vector<int>fam[M];
void get_sa(){
for(int i=1;i<=n;++i) ++c[x[i]=s[i]];
for(int i=2;i<=m;++i) c[i]+=c[i-1];
for(int i=n;i>=1;--i) sa[c[x[i]]--]=i;
for(int k=1;k<=n;k<<=1){
int num=0;
for(int i=n-k+1;i<=n;++i) y[++num]=i;
for(int i=1;i<=n;++i) if(sa[i]>k) y[++num]=sa[i]-k;
for(int i=1;i<=m;++i) c[i]=0;
for(int i=1;i<=n;++i) ++c[x[i]];
for(int i=2;i<=m;++i) c[i]+=c[i-1];
for(int i=n;i>=1;--i) sa[c[x[y[i]]]--]=y[i],y[i]=0;
swap(x,y);
x[sa[1]]=1;
num=1;
for(int i=2;i<=n;++i){
if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k]) {
x[sa[i]]=num;
}
else {
x[sa[i]]=++num;
}
}
if(num==n)break;
m=num;
}
}
void get_lcp(){
int k=0;
for(int i=1;i<=n;++i) rk[sa[i]]=i;
for(int i=1;i<=n;++i){
if(rk[i]==1)continue;
if(k)--k;
int j=sa[rk[i]-1];
while(j+k<=n&&i+k<=n&&s[i+k]==s[j+k])++k;
height[rk[i]]=k;
}
}
int find(int x){
if(fa[x]!=x)fa[x]=find(fa[x]);
return fa[x];
}
long long C(long long x){//很显然对吧
return (long long)1ll*x*(x-1)/2;
}
void val(int r){
static long long cnt=0,maxx=-inf;
//当前集合的height数组都是r，说明排名为x的与排名为x-1的满足r相似
for(auto x:fam[r]){//x名次
int a=find(x-1),b=find(x);
cnt-=C(siz[a])+C(siz[b]);//减去之前的贡献
fa[a]=b;
siz[b]+=siz[a];//将靠前的合并到靠后的集合里
//这形成了一个连接体区间，因为排头兵（设最前面那个下标为y）满足与前面的元素的相似度为height[rk[y]]=i
//那么，就可以说明，这两个区间任取两个元素都满足r相似
//因为如果扩展的话，左边的区间会往左扩展，右边的区间会向右边扩展
//岂不是会变大？岂不是仍然满足r相似
//注意，这里是并查集，千万不要和前面用到的存储height数组的集合弄混了
cnt+=C(siz[b]);//全新的贡献
//维护最次大小值的操作
if(max1[a] >= max1[b]){
//如果a的最大值大于等于b的最大值
//为啥是大于等于，因为我们需要顾及b的次大值是否需要更新（次大值还没更新还不能跑路啊喂）
max1[b] = max1[a];//b的最大值更新
max2[b] = max(max1[b],max2[a]);
//b的次大值只会存在于b的原最大值和a的次大值之中
//毕竟默认的我们已知b的原最大值大于原次最大值
}
else if(max1[a] > max2[b])max2[b]=max1[a];
//b的最大值不会被替代，那么只需要考虑b的次大值会不会被替代
//而且a的最大值大于a的次大值，故只需要比较a的最大值和b的次大值的大小
//如果a的最大值也没戏了，那么a的次大值更没戏了
if(min1[a] <= min1[b]){
min1[b] = min1[a];
min2[b] = min(min1[b],min2[a]);
}
else if(min1[a] < min2[b]) min2[b] = min1[a];
maxx = max(maxx,max(max1[b] * max2[b],min1[b] * min2[b]));
}
if(maxx==-inf)ans[r][0]=cnt,ans[r][1]=0;
else ans[r][0]=cnt,ans[r][1]=maxx;
}
int main(){
scanf("%d",&n);cin>>ss;
l=ss.size();s='0';
for(int i=1;i<=n;++i)cin>>w[i];
for(int i=0;i<ss.size();i++)s+=ss[i];
m=122;
get_sa();
get_lcp();
for(int i=2;i<=n;++i)fam[height[i]].push_back(i);
//下标 lcp -> 储存排名
//将相同相似度的放到同一个集合里
for(int i=1;i<=n;++i){
fa[i]=i;siz[i]=1;
max1[i]=min1[i]=w[sa[i]];/*1正2负*/
max2[i]=-inf;min2[i]=inf;
}
for(int i=n-1;i>=0;--i)val(i);//倒序处理
//为什么倒序，这里给出三种解释
//1，当 r 从大到小减小时，一些原本不相似的酒会变成相似的
//这时就需要将它们合并到同一个分组中，并更新分组的信息
//这样做可以避免重复计算和多余的操作，提高效率
//相似度小的不可能变大，对吧
//2，再者在遍历过程中， height 数组需要取 min 这也从另一个角度说明了需要从大往小枚举
//3,满足3相似的一定满足2相似，以此类推
for(int i=0;i<n;++i) printf("%lld %lld \n",ans[i][0],ans[i][1]);
return 0;
}
