机器人学 —— 机器人视觉(极几何)
极几何是机器人视觉分支——双目视觉中,最为重要的概念。与结构光视觉不同,双目视觉是主!动!测!量!方法。
1、极几何的研究前提
极几何的研究对象是两幅有重叠区域图像。研究目标是提取相机拍摄位姿之间的关系。一旦得到两次拍摄位姿之间的关系,我们就可以对场景点进行三维重建。
极几何定义的物理量包括4个:1、极点,2、极线,3、基本矩阵,4、本征矩阵;定义如左图。
极几何研究的物理量包括4个:C1坐标,C2坐标,R,T,定义如右图。


极点的本质是另一台相机光心在本图像上的映射点。极线的本质是另一台相机光线在本图像上的映射线。(极点和极线都是在图像上的)
1.1、本征矩阵
本征矩阵携带了相机相对位置信息。其推导如下:
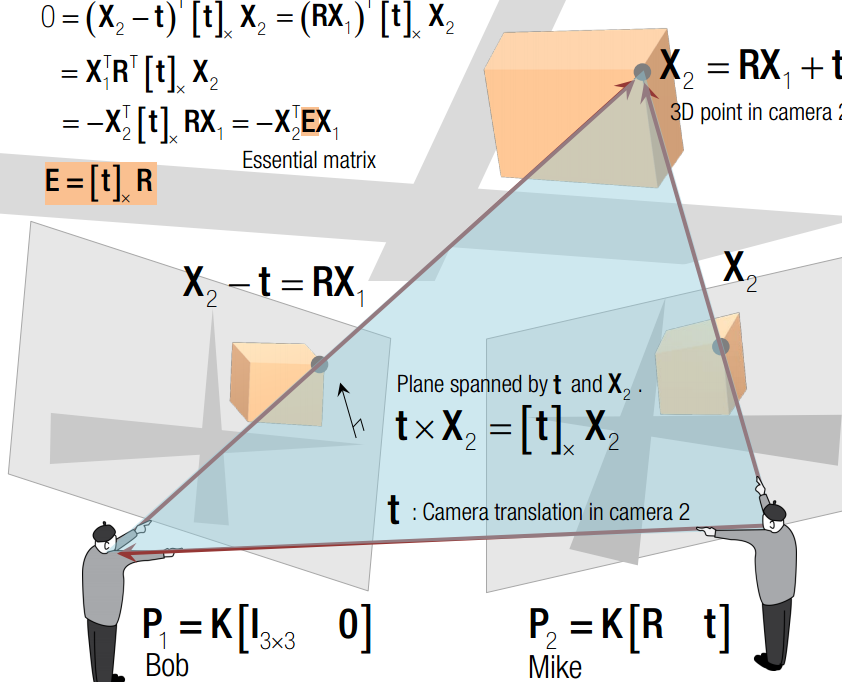
在相机2的坐标系中,场景点坐标:X2 = RX1+ t
相机1光心坐标:t
极线在空间中的映射 :X2 - t = RX1
此时,三个向量在同一个平面上,则有: X2 T tx RX1 = 0
其中,tx 代表 t 的叉乘矩阵。tx R 称为本征矩阵E. 两幅图片一旦拍摄完成R与T都是确定的。空间中任何一组对应点都必须满足本征矩阵!
1.2、基本矩阵
空间中的点满足E矩阵,则该点坐标Zoom后,仍然必须满足E矩阵。坐标的Zoom显然和相机内部矩阵有关。
在相机坐标系下:
x1 = KX1; x2 = KX2
其中,x1 ,x2 是齐次像素坐标。那么,X1 = K-1x1 ;X2 = K-1x2
带入本征矩阵可得:
x2 T K-Ttx RK-1 x1 = 0 ======> K-TEK-1 = 0 =========> x2 T F x1 = 0
F = K-TEK-1 称为基本矩阵。基本矩阵所接受的是齐次像素坐标。
基本矩阵的秩是2,因为它有0空间。同时,其自由度是8,因为它接受的是齐次坐标。每组图像点可以提供1个方程,所以由8组点就可以线性解出F矩阵。当然,解法是化成Ax = 0,然后使用奇异值分解取v的最后一列。然后2次奇异值分解去掉最小奇异值正则化。
1.3、极点与极线
从基本矩阵可知:x2 T F x1 = 0
显然这里有熟悉的身影,由点线对偶可知,x2 在直线 F x1 上。 该直线是极线在图像2上的方程。x1 在直线 x2 T F 。 该直线是极线在图像1上的方程。
极点是多条极线的交点(最少两条)
2、由本征矩阵恢复R,T
E = tx R = [ tx r1 tx r2 tx r3 ]
E的秩为2,因为其有0空间。同时,由于r1 r2 r3 是正交的,所以其叉乘之后必然也是正交的。所以不妨假设其叉乘完之后依然满足旋转矩阵的某些性质。比如:每一列,模相等。
由 tT E = 0 可知,对E奇异值分解之后,t 为最小奇异值所对应的 u(:,end). 如下:
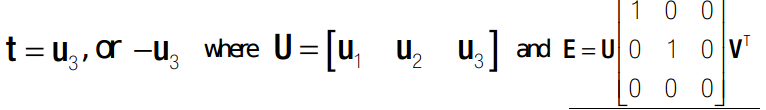
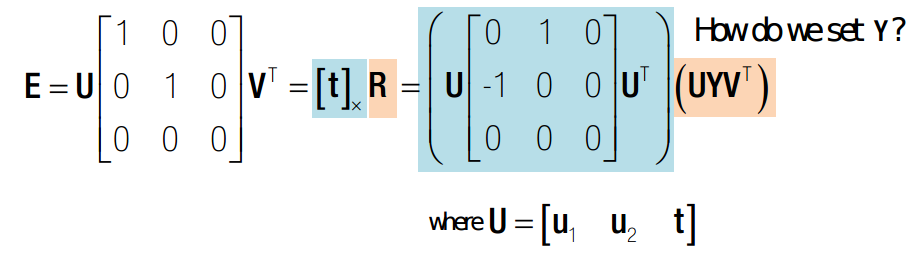

这里假设了 R = UYVT .因为U,V和R是同族的。所以必然由矩阵Y使得上式成立。V是相互垂直的,R的作用是旋转,U则必然是相互垂直的。所以这里R一定有解,不妨设一个中间变量Y。并很容易解得:
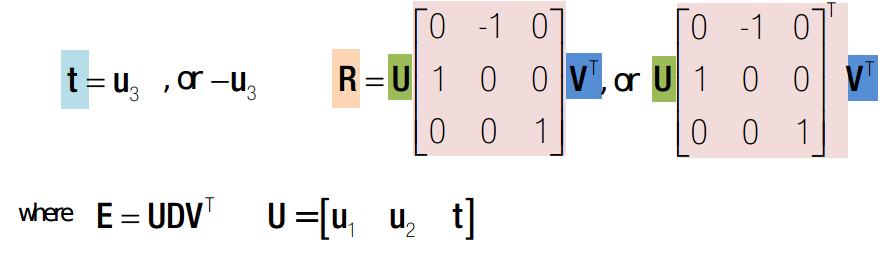
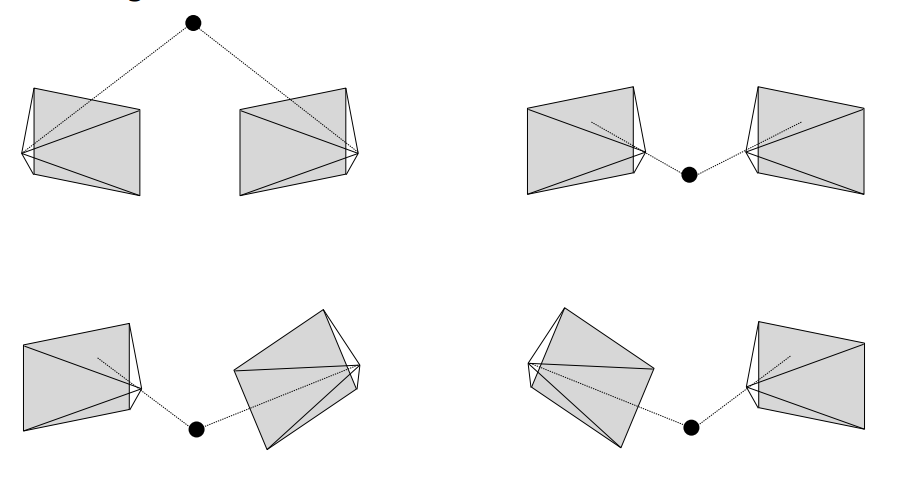
综合来看,由4组可能的解,对应以下四种情况,其中只有第一种是可能的。故det(R) = 1 则猜z中了正确的解,如果det(R) = -1 则解为:t = -t 。R = -R
3、由空间位置关系恢复三维坐标
在已知标定信息,两相机位置关系的情况下,就已知了两个相机的投影矩阵P,对于空间中一点X1,有以下关系:
x1 = P*X1
[x1]x P X1 = 0;
显然,我们又有了Ax = 0的神奇形式。奇异值分解搞定之。
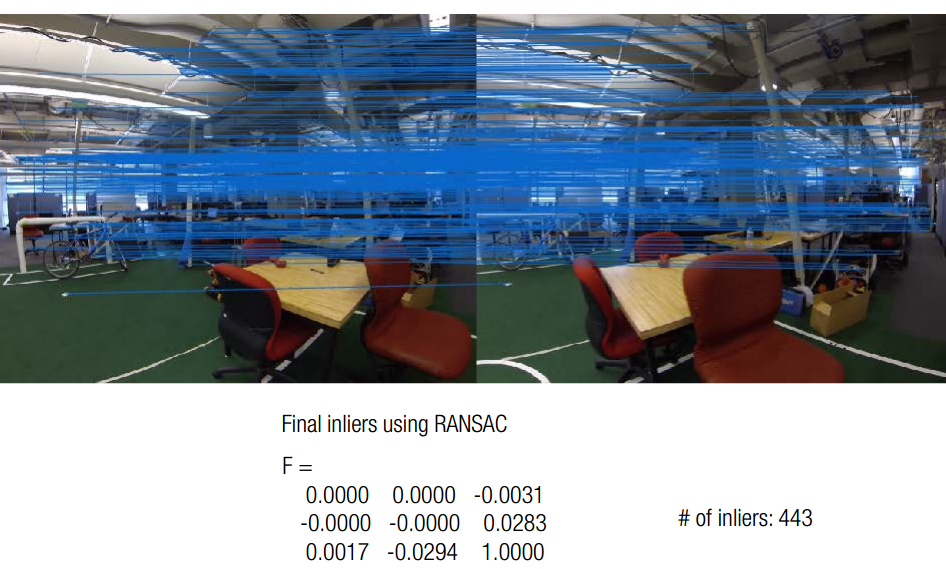
4、由RANSAC求 F 矩阵
有了8个对应点,我们就可以求得F矩阵,再加上K,我们就可以对两幅图片进行三维重建。然而想要自动的求取8个对应点还是有一定难度。
SIFT算法提供了一种自动匹配的可能性,然而,匹配结果还有很多误匹配的点。本节的目标是利用RANSAC作为算法基础,基础矩阵作为方法,来对匹配结果进行判断。
首先,由于检测误差等因素,像素点不可能恰好满足基本方程。所以点到极线会有一定的距离。我们采用垂直距离来建模,有以下表达式:

F1表示F的第一列。只要误差小于阈值,都认为该点符合 F 方程。
算法流程如下:
1、随机取8个点
2、估计F
3、计算所有点的e,并求#inlier
4、回到1,2,3,如果#inlier变多则更新F_candidate
5、迭代很多次结束,F_candidate 为F的估计值
RANSAC算法又一次证明了其对噪声超级好的控制能力。