机器人学 —— 机器人视觉（估计）

之前说到，机器人视觉的核心是Estimation。求取特征并配准，也是为了Estimation做准备。一旦配准完成，我们就可以从图像中估计机器人的位置，姿态。有了位置，姿态，我们可以把三维重建的东西进行拼接。从视觉信息估计机器人位姿的问题可以分为三个大类：1、场景点在同一平面上。2、场景点在三维空间中。3、两幅点云的配准。 所有问题有一个大前提就是知道相机内部矩阵K.

1、由单应矩阵进行位姿估计

　　单应矩阵原指从 R2--R2 的映射关系。但在估计问题中，如果我们能获得这种映射关系，就可以恢复从世界坐标系 x_w 到相机坐标系 x_c 的变换矩阵。此变换矩阵表达了相机相对于x_w 的位姿。

　　H = s*K*[r1 r2 t] —— 假设平面上z坐标为0

　　s*[r1 r2 t] = k^-1*H —— 利用单应矩阵求取旋转与平移向量

　　r3 = r1×r2           —— 恢复r3

　　s 并不重要，只需要对k^-1*h1 进行归一化就能求出来。

　　所以，最重要的就是如何求取两个场景中的单应。在前面我提过从消失点来求取单应关系，但是如果不是从长方形 --- 四边形的映射，我们并没有消失点可以找。

　　这里要介绍的是一种优雅到爆棚的方法。基于矩阵变换与奇异值分解。JB SHI真不愧大牛。三两句就把这个问题讲的如此简单。

　　

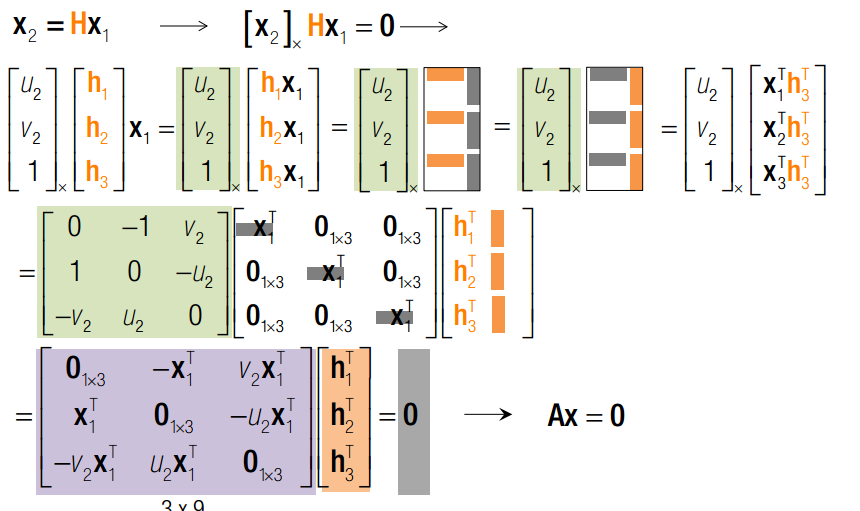
　　由于H矩阵一共有8个自由度，每一对单应点可以提供两个方程，所以4个单应点就可以唯一确定单应矩阵H。Ax = 0,我们在拟合一章中已经了解过了。x 是最小奇异值对于的V矩阵的列。这里是奇异值分解的第一次出现。

　　至此，我们恢复了H矩阵。按照正常的思路就可以解除[r1 r2 t]了。但是，我们的H矩阵是用奇异值分解优化出来的，反解的r1 r2 并不一定满足正交条件，也不一定满足等长条件。所以，我们还要拟合一次RT矩阵。

     此次的拟合目标是 min(ROS3 - R')。其中R' = [k^-1H(:,1:2)  x ]. 方法依旧是奇异值分解，R = UV'. 这是奇异值分解的第二次出现。 

2、由射影变换进行位姿估计

　　由单应矩阵进行位姿估计的前提是所有点都在一个平面上。而由射影变换进行位姿估计则舍弃了此前提，故上一节是本节的一个特例。此问题学名为PnP问题：perspective-n-point。

　　仿造上面的思路，我们依旧可以写成以下形式：

　　

　　此处射影矩阵一共有12个未知数，9来自旋转矩阵，3来自平移向量。每个点可以提供2个方程。故只要6个场景点，我们就可以用奇异值分解获得P矩阵的值。同样，在获得P矩阵后求T = k^-1*P,最后利用奇异值分解修正T.

　　不过按照常理，此问题只有6个自由度（3平移，3旋转）。我们使用6个点其实是一种dirty method.

3、由两幅点云进行位姿估计

　　对于现在很火的RGBD相机而言，可能这种情况会比较多。从不同角度获得了同一物体的三维图像，如何求取两个位姿之间的变换关系。这个问题有解析解的前提是点能够一一对应上。如果点不能一一对应，那就是ICP算法问题了。

　　此问题学名为：Procrustes Problem。来自希腊神话。用中文来比喻的话可以叫穿鞋问题。如何对脚进行旋转平移，最后塞进鞋里。其数学描述如下:通过选择合适的R，T，减小AB之间的差别。

　　

　　T 其实很好猜，如果两个点团能重合，那么其重心肯定是重合的。所以T代表两个点团重心之间的向量。此问题则有如下变形：

　　

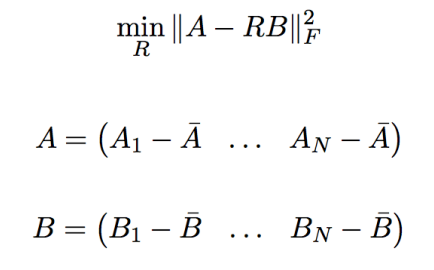
　　由矩阵分析可知，向量的2范数有以下变形：

　　由矩阵分析可知，最后两项实际上是相等的（迹的循环不变性与转置不变性）

　　那么优化目标又可以转为：

　　

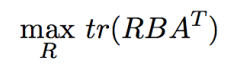
　　迹是和奇异值相关的量（相似变换迹不变）

　　

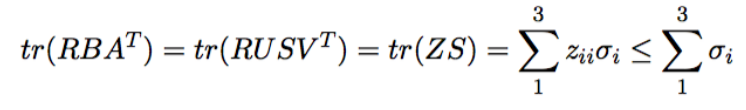
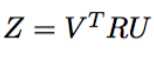
　　显然，如果Z的迹尽可能大，那么只有一种情况，Z是单位阵，单位阵的迹是旋转矩阵里最大的。所以R的解析解如下：

　　

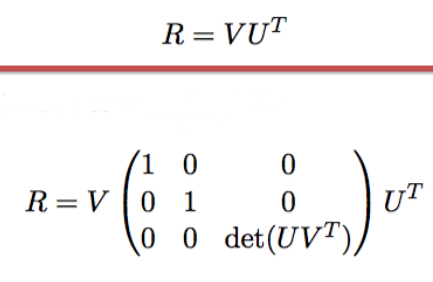
　　至此，我们获得了3D--3D位姿估计的解析解！