机器学习 —— 概率图模型（学习：图结构）

　　概率图模型相比于其他学习算法的优势在于可以利用图结构来将已知信息带入到知识网络中。那么在使用概率图模型之前，往往要求图结构是已知的。而现实中或许我们并没有足够的先验知识，但是有大量的样本。如何通过样本对概率图的G进行推测就是这种学习算法要解决的问题。确实，在有大量样本的情况下，其他的Machine Learning 算法可能可以更方便的解决问题。但是PGM对图模型进行学习的目的往往不是为了使用，而是为了进行Knowledge engineering & scientific.

　　

　　对于学习得到的图模型，有两种错误方式：

　　1、缺失的依赖关系：依赖确实的结果是P(ABCD)错误，该结果下，会得到AD无关的结论。也就是边际掉A对BCD的分布并无影响。

　　2、多余的依赖关系：在多余的依赖关系中，AB之间产生了联系相当于P(ABCD)多乘了一项P(B|A)而少了一项P(B).

　　实际上，对于多余依赖关系的图依然可以正确的对分布进行推测（分布反正就是P(ABCD)，相关关系都摆在那儿了）。但是依赖关系的多余会造成其他步骤变得复杂。多一条边，CPD就会指数爆炸一次。所以依赖关系缺失最终的结果不一定不好。

1、基于分数的学习

　　基于分数学习本质上就是把所可能的G都过一遍，最后选个最高分的。最简单的想法是，正确的图应该让所采集到的数据最可能发生。

　　

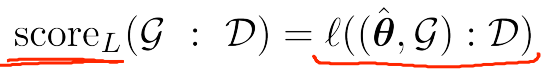
　　也就是要让scoreL尽可能大。此方法的思路是将学习问题转换为优化问题。以multinomial变量为例：

　　

　　此例中使用了log-linear likelihood function.故P的连乘变成了对数相加。在变量集求和又分解成充分统计。最后的到的Ip称为互信息。互信息表达的是两个变量的相关程度。如果相关性很低，则P(x,y)会趋近于P(x)*P(Y).那么其互信息会趋于0.如果两个变量不相关，则其互信息会大于0.实际上，如果直接使用互信息作为优化函数，会有一个问题即：当所有变量两两相连的时候，Score达到最大。这显然不科学，所以为了得到合理的结果，还要使用合适的罚函数。

2、BIC Score

　　BIC Score 使用了一种简单粗暴的罚函数，直接限制学习所得图的维度。

　　

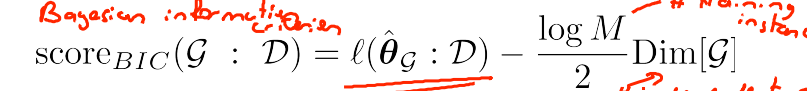
　　在此函数下，M代表训练样本，l为M×Mutual if. 第一项是互信息，使得学习的结果尽可能表达数据集中的关系。第二项是罚函数，是一个与图的维度成正比的量。

　　BIC Score 有一个显著的特征称为渐进一致性。由于第一项是随着数据集的大小线性增长的，而第二项是随着数据集的大小对数增长的，所以在数据集足够大的时候第一项会压过第二项，最终的网络会尽量和数据接近。

　　BIC Score 使用的罚函数称为显性罚函数。

 3、Beyasian Score

　　贝叶斯分数（Beyasian Score)是利用贝叶斯公式导出的一种记分方式，该方式的好处是可以对图先验信息进行导入。使得最终的分数朝着对图先验估计的方向收敛。

　　

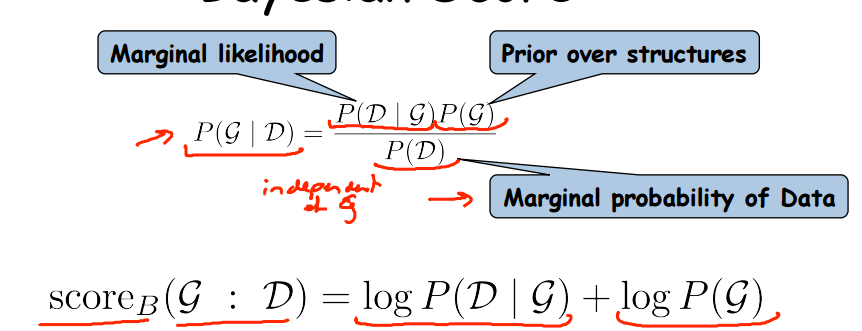
　　贝叶斯分数由两部分组成，第一部分是数据对图模型的拟合程度，第二部分是图的所估计图模型对先验图的拟合程度。

　　其中，数据对图的拟合程度又可以分解成下式：

　　

　　式子的第一部分是似然函数，相当于给定图模型和参数的情况下，数据发生的可能性；第二部分是参数的先验估计，即给定图模型，该参数的可能性。最后把参数边际掉，即是对给定图模型，数据的可能性。

　　如果随机变量是multinomial分布的，那么则可以用狄利克雷函数来对先验参数进行建模。

　　

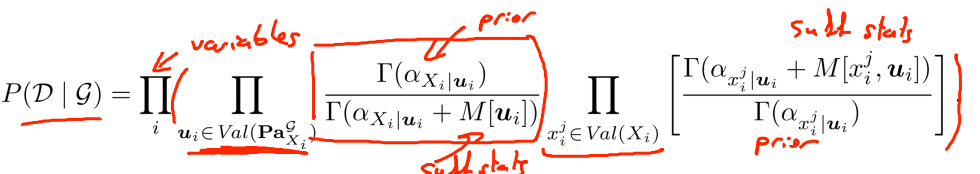
　　P(D|G)实际上是从夫变量到子变量的连乘。最后一项是子变量的每个参数，相当于P(theta|G)，其中分子是对参数的先验估计，分母是是对参数的后验估计。中间项是对图模型建模,分子相当于图模型的先验信息，分母相当于图模型的后验估计。总之，两项相乘表达图模型的局部分数（某个节点及其父节点）。

　　贝叶斯模型的好处是可以对Beyasian Socore的最后一项logP(G)进行调整。具体参数可以是G的边数，或者模型的复杂程度，让最终的分数受到先前对模型假设分数的影响。

4、学习算法

　　学习算法的目的是对图结构进行推测。其本质是一种将Score最大化的方法。其中启发式学习是通过将给定结构加边，减边，逆向边来重新计算分数。

　　图结构的学习算法与概率图模型本身是相对独立的。更注重于算法以及实际调试。故不做过多讨论。