机器学习 —— 概率图模型（学习：CRF与MRF）

　　在概率图模型中，有一类很重要的模型称为条件随机场。这种模型广泛的应用于标签—样本（特征）对应问题。与MRF不同，CRF计算的是“条件概率”。故其表达式与MRF在分母上是不一样的。

　　如图所示，CRF只对 label 进行求和，而不对dataset求和。

1、CRF的likelyhood function

　　

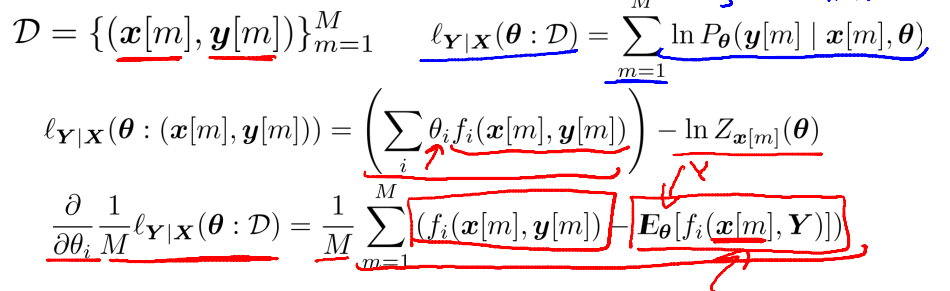
　　对于给定的数据集以及其对应标记，CRF的 E based on theta 是与 数据集 x[m]有关的，因为x[m]并没有完全被边际掉。也就是说，对数据集中的每个数据x[m]，E based on theta 都是不一样的。这是CRF与MRF最大的不同。MRF完全边际掉了x，所以对任意数据集，E_theta 都相同。以图像分割中经典的双牛图为例：

　　 

　　1、图像是聚类后的图像，已经进行了超分割

　　2、X代表超像素，Y代表标签

　　3、Gs代表平均绿强度

　　4、采用loglinear模型：theta*fi

　　对于第一个参数，其仅和特征函数1(f1)有关，求导后发现，第一项是数据集特征统计（数据集特征函数期望）；第二项是在该theta下，数据集对应label = green的概率乘以绿强度。很好理解1函数的模型期望就是概率。

2、CRF与MRF对比

　　1、CRF在训练时，针对每组数据都需要计算E based on model，MRF的E based on model 和单个数据集无关

　　2、CRF在使用时，针对给定x仅需要计算P(Y|x)；MRF计算P(YX)，在计算时需要对XY都进行边缘化。

3、MRF与CRF的先验

　　先验指的是对其参数分布的估计。在贝耶斯多项分布估计中，如果对参数先作出狄利克雷假设，则后续的后验分布也是狄利克雷的。把这个思想移植到MRF与CRF可以对其学习过程的性质进行改善。

　　关于参数的先验有两种，分别是拉普拉斯先验和高斯先验。

　　

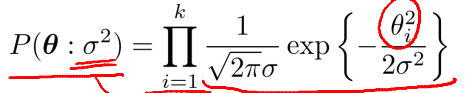
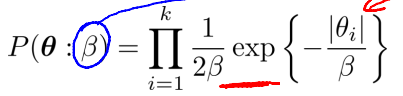
　　其中，delta和beta的作用类似，是分布中的方差。其决定了theta距离0的位置。也就是说该权重的重要程度。而加上先验分布可以带来更好的收敛性。

　　

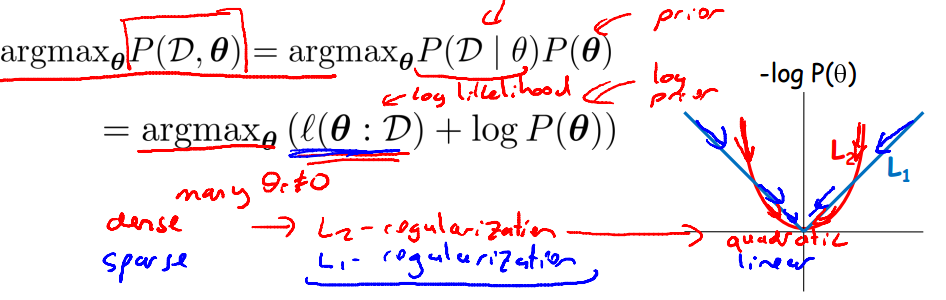
　　如图所示，log函数相当于是一个regularity.在theta被训练集改变的时候，给其一个趋于0的趋势。

　　1、拉普拉斯先验是L1 - regularization， 其有更强的趋势将数据拉向0, 所以利用拉普拉斯先验得到参数会更加稀疏，参数的稀疏性代表fi函数没什么用。换言之，图中连接label和x的边无关紧要，可以去除。

　　2、高斯先验相当于L2 - regularization. 也可以用于对抗过拟合。