机器学习 —— 概率图模型（学习：对数线性模型）

　　对数线性模型是无向图中经常使用的一种模型。其利用特征函数以及参数的方式对势函数进行定义，可获得较好的效果。在之前有向图的学习中，我们发现可以利用d-seperet，充分统计，狄利克雷函数等方式来很优雅的获得参数估计的解析解。但是在无向图中，这些优越的条件都不复存在。而无向图在现实条件下的使用却更为广泛。（这是我第一次在Ubuntu下写博客，感觉好神奇啊，其实说学Linux都是假的，最好的方法就是格掉你的Win,强迫自己在Unix环境下工作。在Ubuntu下截屏喀嚓一声超级有仪式感哈哈哈哈哈，我还学会了在Ubuntu下用python抓网易云音乐，每天都学会神奇的技能哈哈哈）

1、无向图及对数线性模型

　　

　　其中，P(a,b,c) = 1/z * phi(a,b)phi(b,c)显然是由团树分解得到的。l(theta:D)是对上式取对数，并将数据带入后，连乘概率模型得到。第二行将相乘项归类（a1,b1有M[a1,b1]个）。在贝耶斯估计中，分母项中是不包含theta的，而在Markov模型重，Partition Function是包含theta的，而theta又是未知参数，所以无法得到优雅的解析解。

　　对数线性模型如图上所示，其例如图下所示。

　　

　　Z是Paritition Function， theta是参数，fi是特征函数，往往是指示函数，两个变量相关则置为1，否则置为0，描述的是D之间的相关性。

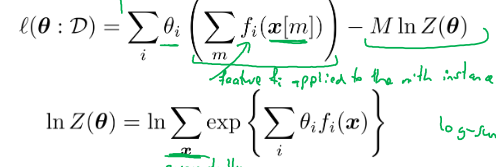
2、对数线性模型的学习

　　显然，在有M重实例的情况下，需要对概率函数进行相乘：这里偷换了一次D的实例，并且交换了一次 i 和 m 求和的位置。原本应该是对一组结果中的i个情况遍历一次特征函数，再对m组进行求和。但此处先利用1个特征函数对数据进行筛选，最后换特征函数再求和。做此种处理的好处当然是有理由求取 l（theta:D) 的最大值。

　　

　　如果在log-linear模型下对thetai 进行求导，有以上性质。并且证得，L函数是一个凸函数。如下所示：

　　两边同除M，则第一项为数据集中特征函数的期望（E[fi] based on data set)，第二项为给定theta参数，特征函数的期望 [ E(fi) based on theta ] 。并且theta的估计正确的前提是数据集特征函数期望与理论期望相符合。由于此函数是凸函数，所以一定可以用优化算法求取其最大值。缺点是每次都需要对基于theta的期望进行求取，每个theta都对应不同的  E[fi] based on theta.

　　以Ising模型为例，上式可以有以下解释：

　　

　　该模型中，theta = wij , ui ，fi = xixj , xi. E[fi] based on theta = xi * p (Xi = xi |theta) . E[fj] based on data set = sigma_x_i /M.

3、总结

　　对数线性模型的估计不存在解析解，但由于其是凸函数，所以可以由优化算法获得。