机器学习 —— 概率图模型（推理：决策）

　　Koller 教授把决策作为一种单独的模块进行讲解，但我认为，决策和推理本质上是一样的，都是在假设已知CPD或者势函数的情况下对模型给出结论。

1、决策==逐利

　　决策的基本思想很intuitive，并且非常有用。在赌博行为中，最后获得的钱与硬币的正反，赌注的大小有关。硬币的正反显然是随机变量，而赌注的大小却是决策量。显而易见的是，决策的最终目的是使得某个期望最大化。再举一个视觉中的例子，对于双目配准算法而言，左相机对应右相机的像素可以认为是随机变量。但是否将两个像素配在一起却可以认为是一个决策（假设像素一一对应，如果甲配了乙就不能配丙了，希望配准的最终结果是尽可能正确的）。故决策的数学表达为：

　　其中，P(X|A)表示在给定决策下，随机变量X的概率。U(x,a)表示给定决策下，x发生所获得的收益。简单的决策如图所示：

　　

2、决策的方法

　　显然从上面的分析可知，我们要做的决策就是使得期望最大化的那个。换一个角度来看，如果每次的决策都是未知的，决策取决于已知信息，决策影响最终结果，如果决策也是随机变量，我们应该把获利最多的那个决策组作为我们所需采取的决策库。换而言之，凡事应有a,b,c三策，不同的策略对应不同的情况。显然，我们所需要采取的策略取决于已知的信息（Action的父节点）。而策略组本身就是一个随机变量。

　　

　　如图所示，如果变量真实值无法观测，只能通过一个传感器（survey）来进行推测时，决策应该取决于S的值。S的值又和其所有父节点（M）的值相关。MEU表示所选择的策略。

　　

　　

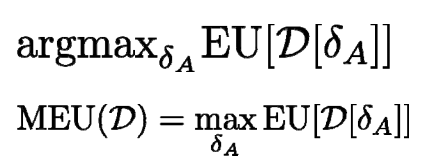
　　显然，我们需要P(S)deta(F|S)U(F,M)，然后P(S)需要对P(M,S)进行边际获得。故表达式如上。带入数据发现

　　如果想要上式最大，则deta(F|S)为正。其正值表示倾向于决定.....

　　故，决策为s0->f0,s1->f1,s2->f1

3、决策函数与人性

　　决策实际上是非常重要的一个环节，其会影响最终的收益期望。决策的目标是使得收益最大化。但是，人类并不是这样决策的，古语云：千羊在望，不如一羊在手。又云：蚊子肉也有毒死人的时候（比如中国国家队VS皇马，大部分人肯定买皇马赢）。决策函数也是值得研究的。单纯的计算期望可能无法模拟人的行为。

　　

　　图中实线是人的决策曲线，U表示的是Utility。也就是“人们眼中”决策带来的收益期望，横坐标是实际期望。完全理性的情况下，“满足期望”与实际期望应该是匹配的。但是人在决策的时候如果概率是0.5,人会觉得如果有人出400买自己的彩票就卖了。也就是U = 400与正常情况下p=0.5&线性u是等价的。400~500之间称为保险收益。

　　典型的决策曲线如图所示：
　　　　古语云：见小利而忘义，干大事而惜命是也。当损失可能性较小时，人们的容忍程度非常高，当收益较小时，人们可能会保守。实际上，千羊在望与一羊在手也是一个边际问题，穷人往往会选择一羊在手，因为他没有啊。如果我本身有一千头羊，赌赢了我就有两千头，为什么不赌？所以可以把决策作为边际收益的函数，来构造决策方案。

4、信息的价值

　　决策的前提是观测，观测往往是有成本的。例如做调研需要资金，做检查需要资金。甚至实时机器人系统如果需要一个准确的定位可能需要停下来，这也是成本。那么在决策前就需要判断决策的必要性，如果决策带来的收益大于决策成本，则决策是划算的。这个多出来的收益称为信息的价值VPI(value of perfect information).

　　1.VPI永远是大于等于0的。perfect information 表示其不是错误的信息，一定正确的信息肯定会使得收益有所增加。

　　2.当且仅当决策不变时，VPI为0，比如你提供给我1年的某网站财报，我还是会选择去谷歌。

　　图中s表示公司状态，f表示公司所获得资助。公司1获得资助期望为0.72，公司2获得资助期望为0.33.

　　如果对公司2进行观测，当且仅当公司2为s3时，会改变主意，其获得资助期望变为0.9.

　　那么，信息观测收益就是 （0.9-0.72）*0.1 = 0.018

　　　　

　　如果此情况，则观测收益为（0.4-0.35）*0.5+（0.9-0.35）*0.1 = 0.08

 

　　实际上，信息观测只在两个状态旗鼓相当的情况下收益比较高。悬殊很大的时候，信息观测并没什么意义。