PCL—低层次视觉—关键点检测（NARF）

　　关键点检测本质上来说，并不是一个独立的部分，它往往和特征描述联系在一起，再将特征描述和识别、寻物联系在一起。关键点检测可以说是通往高层次视觉的重要基础。但本章节仅在低层次视觉上讨论点云处理问题，故所有讨论都在关键点检测上点到为止。NARF 算法实际上可以分成两个部分，第一个部分是关键点提取，第二个部分是关键点信息描述，本文仅涉及第一个部分。

　　在文章开始之前，有非常重要的一点要说明，点云中任意一点，都有一定概率作为关键点。关键点也是来自原始点云中的一个元素。和图像的边缘提取或者关键点检测算法追求n次插值，最终求的亚像素坐标不同，点云的关键点只在乎找到那个点。

1. 边缘提取

　　首先声明本文所有思想算法公式均来自：Point Feature Extraction on 3D Range Scans Taking into Account Object Boundaries 

　　在正式开始关键点提取之前，有必要先进行边缘提取。原因是相对于其他点，边缘上的点更有可能是关键点。和图像的边缘不同（灰度明显变化），点云的边缘有更明确的物理意义。对点云而言，场景的边缘代表前景物体和背景物体的分界线。所以，点云的边缘又分为三种：前景边缘，背景边缘，阴影边缘。

　　rangeImage 是一个天然适合用于边缘提取的框架。在这里需要做一些假设：每个rangeImage像素中假设都只有一个点（显然在生成rangeImage的时候点云是被压缩了的，压缩了多少和rangeImage的分辨率有关，分辨率不能太小，否则rangeImage上会有"洞”，分辨率太大则丢失很多信息）。

　　三维点云的边缘有个很重要的特征，就是点a 和点b 如果在 rangImage 上是相邻的，然而在三维距离上却很远，那么多半这里就有边缘。由于三维点云的规模和稀疏性，“很远”这个概念很难描述清楚。到底多远算远？这里引入一个横向的比较是合适的。这种比较方法可以自适应点云的稀疏性。所谓的横向比较就是和 某点周围的点相比较。 这个周围有多大？不管多大，反正就是在某点pi的rangeImage 上取一个方窗。假设像素边长为s. 那么一共就取了s^2个点。接下来分三种情况来讨论所谓的边缘：

　　1.这个点在某个平面上，边长为 s 的方窗没有涉及到边缘

　　2.这个点恰好在某条边缘上，边长 s 的方窗一半在边缘左边，一半在右边

　　3.这个点恰好处于某个角点上，边长 s 的方窗可能只有 1/4 与 pi 处于同一个平面

　　如果将 pi 与不同点距离进行排序，得到一系列的距离，d0 表示与 pi 距离最近的点，显然是 pi 自己。 ds^2 是与pi 最远的点，这就有可能是跨越边缘的点了。 选择一个dm，作为与m同平面，但距离最远的点。也就是说，如果d0~ds^2是一个连续递增的数列，那么dm可以取平均值。如果这个数列存在某个阶跃跳动（可能会形成类似阶跃信号）那么则发生阶跃的地方应该是有边缘存在，不妨取阶跃点为dm(距离较小的按个阶跃点）原文并未如此表述此段落，原文取s=5, m=9 作为m点的一个合理估计。

　　对任意一个点，进行打分，来判断该点作为边缘点有多大可能性。首先，边缘可能会在某点的：上，下，左，右四个方向。

　　所以只要把pi 和 pi 右边的点求相对距离。 并把这个相对距离和dm进行比较，就可以判断边缘是不是在该点右边。如果距离远大于dm，显然该点右边的邻点就和pi不是同一个平面了。

　　

　　为了增加对噪声的适应能力，取右边的点为右边几个点的平均数。接下来依据此信息对该点进行打分。

　　其中deta 就是dm. dright = || pi pright ||. 

　　最后再取大于0.8的Sright，并进行非极大值抑制。就可以得到物体的边缘了

　　

2. 关键点提取

 　  在提取关键点时，边缘应该作为一个重要的参考依据。但一定不是唯一的依据。对于某个物体来说关键点应该是表达了某些特征的点，而不仅仅是边缘点。所以在设计关键点提取算法时，需要考虑到以下一些因素：

　　i) it must take information about borders and the surface structure into account;

 　　边缘和曲面结构都要考虑进去

     ii) it must select positions that can be reliably detected even if the object is observed from another perspective;

       关键点要能重复

　　iii) the points must be on positions that provide stable areas for normal estimation or the descriptor calculation in general.

　　　关键点最好落在比较稳定的区域，方便提取法线　

　　对于点云构成的曲面而言，某处的曲率无疑是一个非常重要的结构描述因素。某点的曲率越大，则该点处曲面变化越剧烈。在2D rangeImage 上，去 pi 点及其周边与之距离小于2deta的点，进行PCA主成分分析。可以得到一个 主方向v，以及曲率值 lamda. 注意， v 必然是一个三维向量。

　　那么对于边缘点，可以取其 权重 w 为1 ， v 为边缘方向。

　　对于其他点，取权重 w 为 1-(1-lamda)^3 ， 方向为 v 在平面 p上的投影。 平面 p 垂直于 pi 与原点连线。

　　到此位置，每个点都有了两个量，一个权重，一个方向。

　　将权重与方向带入下列式子 I 就是某点 为特征点的可能性。

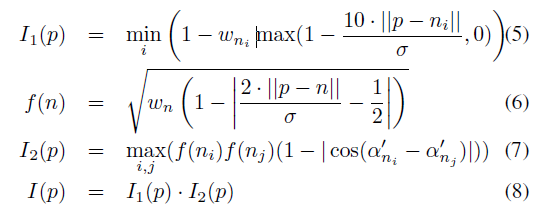
　　最后进行极大值抑制，就可以得到一些特征点了。

3. 关于特征点提取的一些思考

　　在我看来，本文提出的算法效果上可能确实不错，但是这算法里面太多经验值与神秘数。各种式子没有明确的物理意义，只是单纯为了获得一个较好的结果设计出来 "打分"的。 这种算法实在谈不上优雅，当然，我连这种不优雅的算法也设计不出来。。。。。。。

　　点云的特征点提取应该与后面的特征描述是松耦合的。确实不得不承认，针对不同的点云：稀疏的，致密的，有序的，无序的，有遮挡的，高精测量的.......设计不同的关键点提取算法也无可厚非。总结出的关键点提取算法原则就是要尺度不变，鲁棒性好，至于是否一定要存在于平坦区域，我觉得并不一定。不同的关键点提取算法可以和不同的特征描述算法进行组合，最终得到一个较好的效果。如果非要把关键点提取算法和特征描述算法紧耦合，那势必会失去一部分灵活性。

　　最后还有一点想要吐槽的是，点云中的点为什么不应该自带是否是关键点的性质，而需要我们来进行检测？这显然不符合面向对象的设计原则........我觉的应该有某种点云采集方法，得到的点云可以有以下性质：

　　point.is_key_point = 1/0.

　　这多好~