机器学习 —— log-linear 模型
昨天刚刚解决了 logistic regression 之后今天又来了个有趣的家伙。 logistic regression 很强大,但是也有它的弱点。它最大的弱点就是只能告诉你是或者不是,而无法告诉你 XX is YY.这对于追求人工智能来说,只能是走出了一小步。在解决 YES/NO 的问题之后,我们还需要解决 WHAT 这个问题。 聪明的计算机科学家(也许是数学家)又设计了一种新的模型,这种模型可以告诉我们 WHAT。也就是 log-linear 模型。
——离真正的人工智能还很远,或许它是一个科学问题而不是一个工程问题,记我学习 Mechine Learning 的第二天
1、Log-linear
如果要计算机告诉我们WHAT,按照之前的思路,还是应该从概率入手。应该是找到某个模型,模型的输入是一些信息,模型的输出是the label在已知信息下的可能性。这个模型里有参数,不同的label对应不同的参数。对于测试目标,我们只要比较它-->model(the para) 后得到的概率,就可以推断它和哪个label比较配。label应该是有限的。接下来的任务就是找the label 对应的参数。
这组参数应该使 p(y|x;w)达到最大,其中 y 是what:洗衣机,台灯,冰箱、、、、x 是样本:颜色,形状,大小,重量,价格,材质......
概念我们有了,接下来就只有一个问题:这个模型长什么样。既然是个概率模型,那我觉得首先有两个重要特征:
1.它应该不只一项,最好每项都能表达 <label - 维度> ,样本有d个维度,这个方程应该有 d 项,毕竟我们总是希望我们的各种样本维度在计算时不是耦合的。
2.它的取值范围应该在0~1之间,因为它是概率。
接下来我们就要设计一个有着优良数学性质的模型,毕竟我们还要对参数求导算梯度呢。。。。搞个很复杂的东西怎么行。。。。
首先,这次的方程不再是x一个人的事情,因为y也是多样的:那么对于某一项应该表示成: Fij(x_i,y_1).
其次,这些项应该是相加关系,我们用权重来控制这一项对 p(y_j|x)的贡献, 也就是说,这些项的“合成效果”应该表达成 :Wij是各个项的权重.
i = 1:d j=1
∑Wij*Fij(x_i,y_j)
接下来,上面那一堆和的结果都不一定是正的,所以我们首先要保证它大于0,老办法取指数: exp(∑Wij*Fij(x_i,y_j))
最后,如果再想办法让整个东西小于1,那它就基本符合我们的要求了,怎么搞? 显然,把所有词性都算一遍再求和,就会大于单个词性。
实际上,我们拼出来的就是log-linear模型。
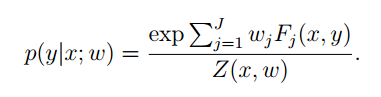
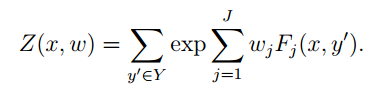
那么在给定一个训练集时,我们要使得the label判断最准确,应该让p尽量大。本质上就是让分子尽量大,我们就有了训练的目标:
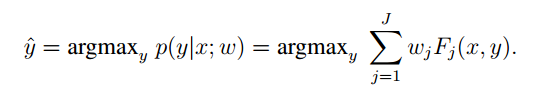
于是乎还剩下最后一个问题,如何确定 F
2.特征方程 F
F 被称为特征方程,它一共有 C*d个,C是标签数,d是样本维度。也就是说,每个维度都是和特征有关的。
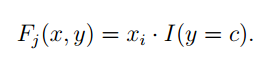

i=1~d, c=1~C
也就是说,Fj对应了所有的label,每个label 有d个F. 是不同的。这样可以自动生成需要的所有Fj(洗衣机对应1~d号的话,电吹风会自动对应d+1~2d号。。。),上述是一种Naive的Fj设置方法,它认为只有当y取某个特定标签时,才使用Fj中的某些项,当y取其他标签时,这组权重是被屏蔽的。例如:我们在讨论某个物体是不是洗衣机时,电吹风的训练权重就被屏蔽了。这本质上就是很多很多logistic regression 并联在一起。
为了方便使用,做以下设计:F--->0/1。很好理解,某个标签和某个样本维度要么有关要么无关,至于最后会是多少由权重调节。
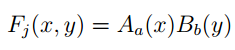

这里是为一个词进行词性判别,A1~A4是和名词判别有关的Function这里的B(名词)就应该全部取1,选通A1~A4,屏蔽其他
A5~A8可能会是和动词有关的判别了,如果y=动词 被选通,则屏蔽和名词,形容词等有关的判别。



