机器学习 —— 极大似然估计与条件概率
今天在研究点云分割的时候终于走完了所有的传统路子，走到了基于机器学习的分割与传统自底向上分割的分界点（CRF）算法。好吧，MIT的老教授说的对，其实你很难真正绕过某个问题，数学如是，人生也如是。
---记我的机器学习之路
1、机器学习
在之前的学习过程中，机器学习对我而言实在是洪水猛兽般的存在。很多玄玄乎乎的公式，算法，各种算法的名字一看就比较高级；如黑箱一般的过程；摸不清的物理意义；繁杂的公式实在是让人头大。为了能更好的学习PGM，我决定放弃由从神经网络或者深度学习一类的算法入手的打算，改由统计，概率与推断入手，来学习Learning. 实际上如果你只看中利用机器学习来做什么，那么完全不需要头疼它到底是怎么Learning的，Learning已经成了一个抽象类，对所有的问题都可以用：
Learn graph_learn(new learn::graph_learn); learn.train; learn.app; learn.result;
的方法来完成。至于how to train,how to extract result，显然已经被各路大神封装的妥妥的了。但是如果真的想要从机器学习中获得启发或者是将其与自己的专业结合的更紧密，可能还是要对这个东西开膛破肚吧。
2.极大似然估计
估计（estimating）是一种手段，一种对模型参数进行推测的手段，说白了，就是利用训练数据对模型进行calibration. 在标定之前，首先需要有一个模型。模型中需要有待辨识的参数。极大似然估计是 现象--->原理 的过程，这个世界上已经发生的，都必然会发生（given by Kang.YH_HUST)。遵循这个原理，求解模型参数就成了一个寻优的过程。当给定模型与结果，时间发生的概率p是参数a的函数。其原理如下：
f(x1, . . . , xn; θ) = ∏ fθ(xj ; θ).
L(θ; x1, . . . , xn) = f(x1, . . . , xn; θ).
θ = argmaxθ L(θ; x1, . . . , xn).
由于模型是已知的，那么对给定观测值，其对应概率p是可以表达的。根据此原理可以求解以下两个问题：
1.如果θ是二项分布的参数，那么在给定一组结果的情况下，似然函数L可表达为：
对似然函数求导，可得当θ=h/n时似然函数取最大值。h是x=1的次数，n是实验总数。
2.如果L函数是线性的，那么可以对L函数取对数，取完对数后结果是一样的。
3.条件似然估计
说到条件概率，好像事情就变得有点复杂， y|x 总是给人一种先有x后有y的感觉，但其实x,y并不是先有鸡后有蛋的关系，x,y应该理解为y受到x的约束，会随着x的改变而改变y的取值。条件所表达的意义在于约束，而非顺序。 如果用约束来解释这个关系，那么接下来的事情就好理解了：
1、如果 y 受到 x(向量）的约束，y的取值是随着x变化的。
2、为简化约束，假定：x 各个分量对 y 的约束是线性组合的，不同的分量有不同的权重。
上面是一个简单粗暴的模型，x 的各个分量可以看作是 x的不同特征。
比如：点云颜色，点云密度，点云曲率 都可以看作是对 该是否该出现（0 1问题）有影响，那么就可以设计基于条件概率的点云滤波器。
有了上述概念以后，就需要把它量化，有两点需要量化：
1.x的加权和在哪个范围。
2.如何让y的概率落在0~1。
显然 logistic regression model 能够很好的解决量化问题：
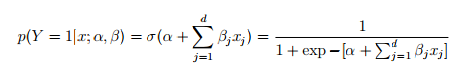
对 x 各个部分的权重而言，取值可以从 负无穷到正无穷；
对 y 的概率而言，取值用于在0~1之间。
这个系统中，需要辨识的参数就仅仅是beta(alpha可以看作是beta0,x0=1)，要辨识beta并不是一件容易的事情，对所有给定x，我需要算出它对应的p，并把表达式相乘，再优化求解。显然这是笨办法，先对L(beta)函数做些处理才是上策。
因为对Y而言，其为二项分布（丢硬币要么正面要么反面，但是硬币可以有bias，这个bias可以由很多事情决定），二项分布的极大似然估计是已知的：
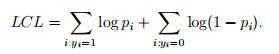（似然函数取了对数）
如果等式两项同时向beta求导，则有：
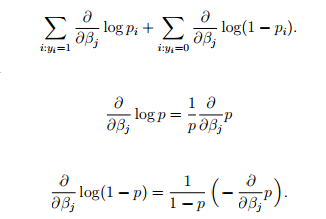
p不仅仅是p，p还是beta的函数：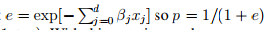
，那么则有：
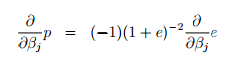
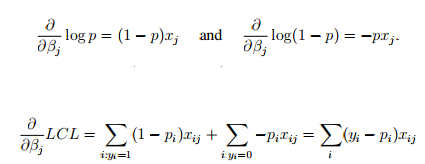
OK,好像令上式为0,则可求出beta对xij,yij的表达式。。。。。然而却没有那么简单。
3、学习，机器也抄近道
这个东西不那么简单的原因在于pi是一个非常复杂的表达式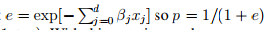：。虽然任意一个beta都是独立的，但是要把所有的xi全部代进去，再求最小值也没那么简单，虽然这个最小值肯定存在，但如果没有beta，你也算不出来啊。。。陷入了该先拿身份证还是先开锁的困境中。
所谓的学习（training），本质上是一种数值求解方法。一般情况下，可以表达为梯度下降法，它是这样的：
在已经假设了beta(向量）的初始值情况下，beta(j) 的梯度是已经得知了的。那么对 整个训练集（i）全部遍历一遍就可以算出梯度，由梯度再刷新Beta_j。伪代码大约如下：
while ( all_beta != coverge)
for j = 1:end_of_features
for i = 1:end_of_training_set
Partial_Beta_j += (yi-pi)xij
end beta(j) = beta(j) + lamda*Partial_Beta_j end
end
显然，这很不科学，对每个beta(j)我都需要遍历整个训练集，最后才改变了一点点。。。。。然后我又要遍历整个训练集。。。。。如果训练集很大，那岂不是坑爹。
所以我们需要一个抄近道的方法，成为随机梯度下降法。这个方法的原理其实很简单：训练集包含的信息是一致的。
不是一样的，是一致的。假设我们能找到一个随机变量Z，使Z满足：
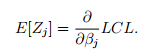
那么，只要Z的取值次数够多，我们就可以利用Zj来替代E[Zj](取足够多次，那么他们最终效果的相同的）
不妨取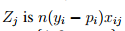
。由于n是一个常数（训练集的规模）。那么Beta(j)也就变成了：
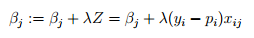
终于，整个训练过程被简化成了：
1.for epcho = 1:3 2. for i = 1:end_of_training_set 3. for j = 1:end_of_features Partial_Beta_j += (yi-pi)xij beta(j) = beta(j) + lamda*Partial_Beta_j end end train_set.rand_rank(); end
其中，epcho被用作强制收敛，一般是3~100。第二个 for 和第三个 for 是可以对调位置的。据说会导致收敛变慢，该方法叫做cordianate ascent.
Ok,学习的问题基本上解决好了，还抄了点近道，想想就有些小开心~接下来还要解决1个扫尾的问题，搞定了的话我们也算玩过机器学习啦啦啦啦~~~
问题：如果训练集合处处点云密度 为 1，且只要这个特征出现，点云就被认为是 无效的，那么随着训练的增加beta就会一直上升，直到无穷大；
当然，当训练集非常合理，特征量化也非常合理的时候上面的那个问题不会出现，但显然不会如此十全十美。
所以简单粗暴的引入一个惩罚因子，来防止beta跑飞.
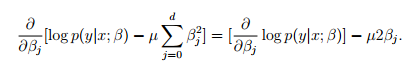
u是常数，当beta过大或者过小的时候惩罚因子能起到纠偏的作用，但结果会带来误差。
4、将简单的机器学习用于点云滤波
显然上式我们已经得到了beta 关于xij,yi的表达式，接下来要做的很简单：
1.量化曲率x1，颜色x2，密度x3（根据经验，都要在-1~1之间，方差最好为1）。
2.指定一些点，是，或者不是某点云的点y（0/1)
3.训练。
我们就得到了一个判断某点是否属于该点云的一个简单“判别器”（本质上就是个概率函数），当遇到某个点时，可以算它是有效点还是无效点的概率。
其实机器学习没有那么难~也没有“黑”~~~~
