如何使用现有工具三分钟之内从无到有设计一款滤波器？
写在前面
前些天看了一本漫画，里面一个老技术人员的话，让我不自觉的想到很多东西。
是啊，有时候我们自认为的自我实现，其实就是在凑这个时代的热闹，每个时代都有自己的热闹，个人之于时代不过是浪花一朵朵。
但这并不能作为我们不去凑这个热闹的理由，你去凑时代的这个热闹，这个时代必会给予你奖励，或早或晚，或大或小，终会来到。
这周给大家分享，前段时间设计滤波器时碰到的一些问题和解决办法，希望对大家有帮助。
完整的流程图如下：
什么是滤波器？
看过我以前博客的都知道，我研究方向是研究谐波的，一个人类靠肉体看不到也摸不着的东西，但它确实存在。
具体什么是谐波，感兴趣的同学可以下去自己了解，这里我们只需要知道，这玩意有好处，也有坏处，关键看用在什么地方。
我们的目的是消灭那些我们不想要的谐波。
对此，第一个闪进我们视野的就是——滤波器。
减小谐波影响应对谐波源本身或在附近采取适当的措施，通常情况下，采用加装滤波器的方式治理谐波。
滤波器一般分为无源滤波器和有源滤波器。
首先滤波器按照处理信号类型分类有模拟滤波器和离散滤波器，而我们常用的模拟滤波器又分为有源滤波器和无源滤波器。
有源与无源的对比
1.谐波处理能力
无源滤波器只能滤除固定次数的谐波；但完全可以解决系统中的谐波问题，解决企业用电过程中的实际问题，且可以达到国家电力部门的标准；有源滤波器可动态滤除各次谐波。
2.系统阻抗变化的影响
无源滤波器受系统阻抗影响严重，存在谐波放大和共振的危险；而有源滤波不受影响。
3.频率变化的影响
无源滤波器谐振点偏移，效果降低；有源滤波器不受影响。
4.负载增加的影响
无源滤波器可能因为超载而损坏；有源滤波器无损坏之危险，谐波量大于补偿能力时，仅发生补偿效果不足而已。
5.负载变化对谐波补偿效果的影响
无源滤波器补偿效果随着负载的变化而变化；有源滤波器不受负载变化影响。
6.设备造价
无源滤波器较低；有源滤波器太高。
有源电力滤波器
在研究这个滤波器的时候，我还碰到了一个很有意思的滤波器，叫有源电力滤波器，经常用在电网里，一开始我还把它和上面那个有源滤波器搞混了。
有源电力滤波器（Active Power Filter，简称APF）是一种用于动态抑制谐波、补偿无功的新型电力电子装置，它能够对大小和频率都变化的谐波以及变化的无功进行补偿。
内部原理图如下：
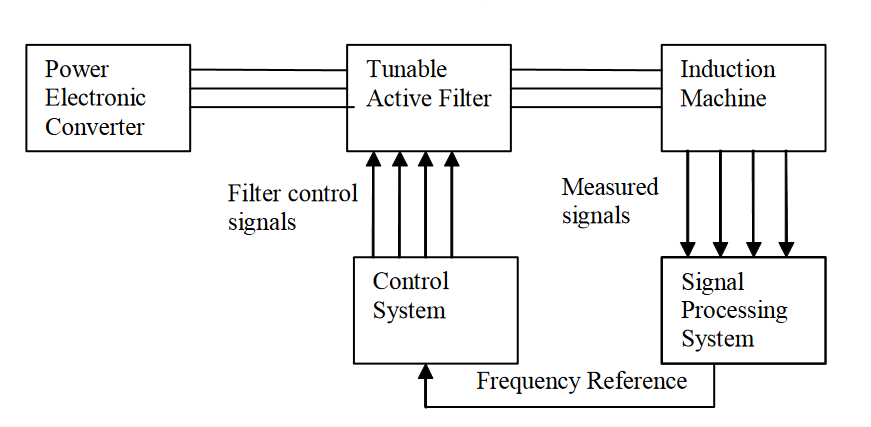
它是通过外部电流互感器，实时检测负载电流，并通过运算器，提取出负载电流的谐波成分，然后通过PWM信号发送给内部IGBT，控制逆变器产生一个和负载谐波大小相等、方向相反的电流注入到电网中补偿谐波电流，实现滤波功能。
也是非常有趣的东西，但它不是我这次要讲的重点，以后有机会可以再聊聊。
第一步：网页工具设计滤波器
现在网上有很多可以辅助我们进行设计的工具箱，甚至不用你安装任何东西，网页版就可以，连VScode都有网页版的了，还有什么是不可能的。
这里给大家推荐两个可以进行滤波器设计的网页工具箱。
首先是亚诺半导体官网的：点这里
https://www.analog.com/cn/design-center/design-tools-and-calculators/amplifier-and-linear-tools.html
我用的最多的还是TI官网的这个：点这里
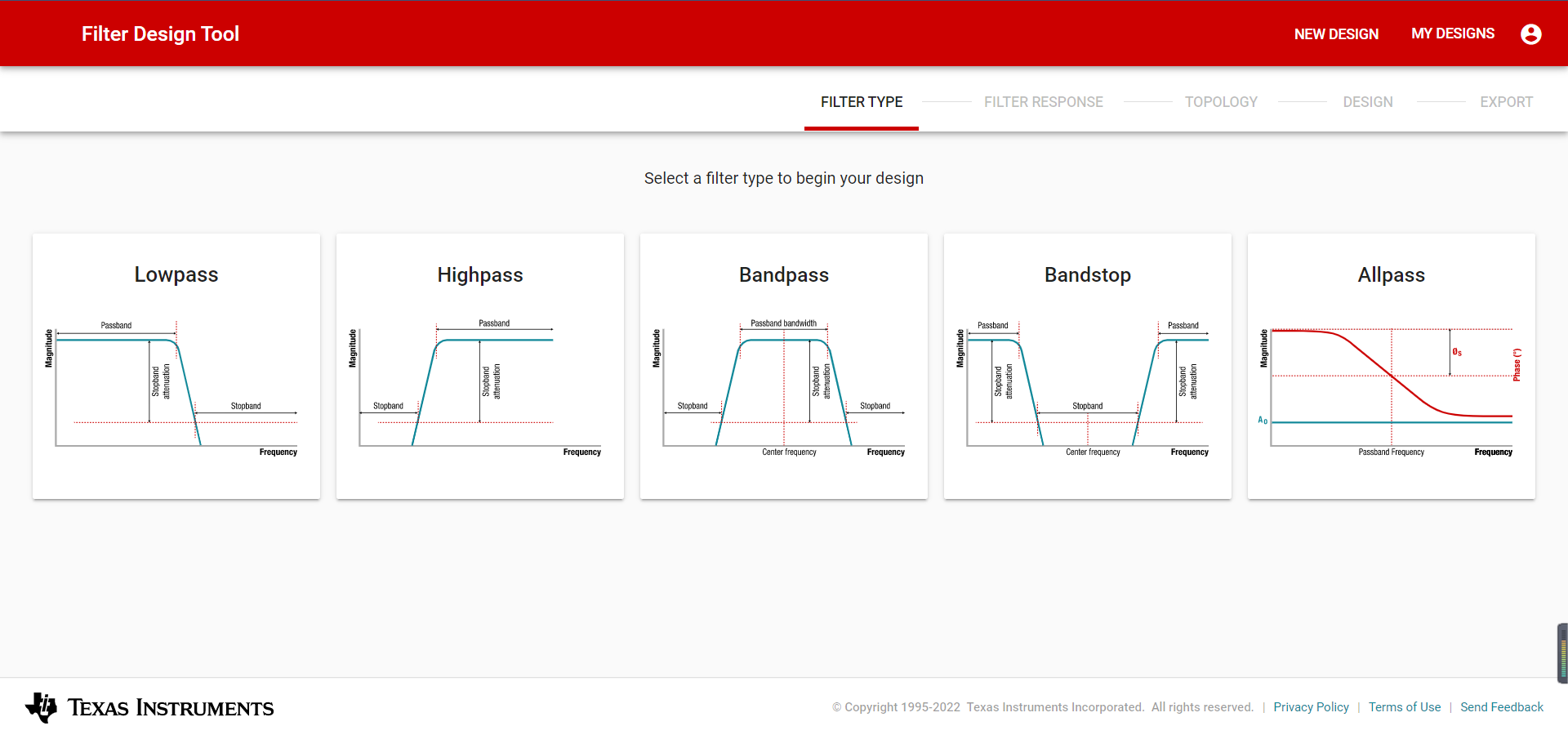
简单给大家说一下流程：
咱们先定一个设计目标：50HZ+1.3KHZ 滤除1.3KHZ
1.1选择滤波器类型
低通滤波
1.2根据需求确定以下参数
通带增益、通频带、通频带起伏、阻带、和阻带衰减量
有这样一个设计的准则：
过渡带（阻带fs-通带fc）越窄，期望的阻带衰减Asb越大，所需要的滤波器级数order越多，所需元器件越多。
1.3选择滤波器的响应
常见的滤波器响应有三种：
- Bessel拥有通频带内恒定的时延，但截止速率最慢;
- Chebychev拥有最陡的截止速率，但通带起伏最大;
- Butterworth拥有最平坦的通频带，和较好的通带起伏。
巴特沃兹滤波器比较合适。
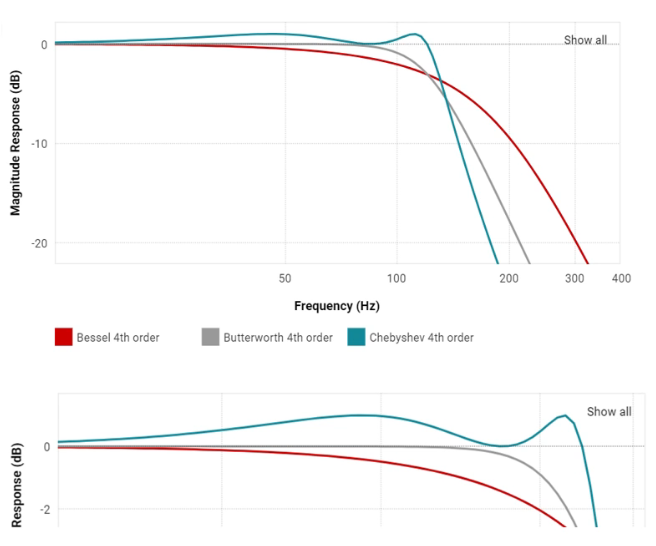
设计之后的频率响应曲线：
order阶数，所需运算放大器个数；
Q对方波冲击响应的一个稳定性。
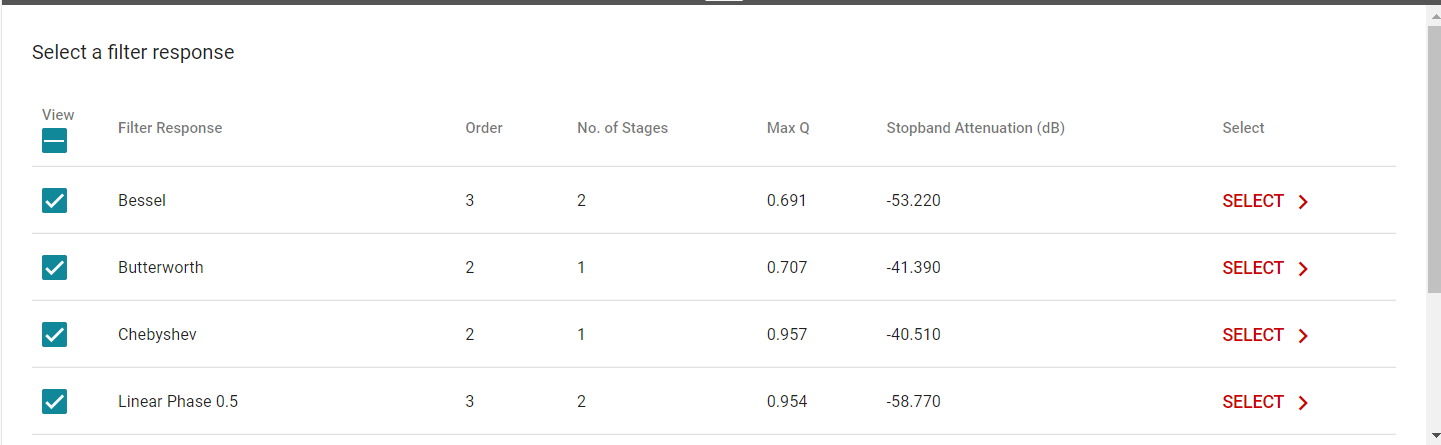
1.4选择滤波器的拓扑
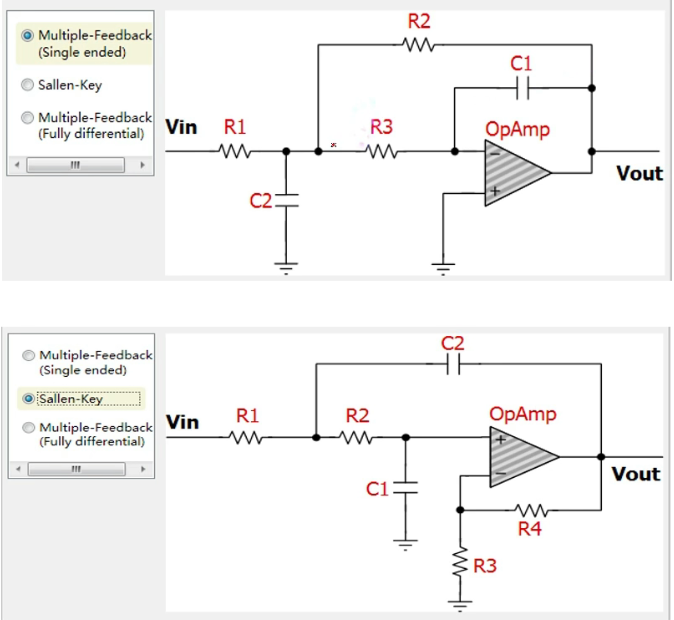
常见滤波器的拓扑有两类：
Multiple - Feedback (MFB)
- 输入输出反相
- 输入阻抗低，输出阻抗低
- 无高频馈通，对运放带宽要求低
- 不需要额外的增益电阻对器件敏感度低
Salley-Key
- 输入输出同相
- 输入阻抗高，输出阻抗低
- 有高频馈通，对运放带宽的要求更宽
两者最本质的区别：输入输出的相位方向
1.5根据器件的获取难度和成本来确定器件的值
关键是电阻电容的一个精度问题，保证在10%左右。
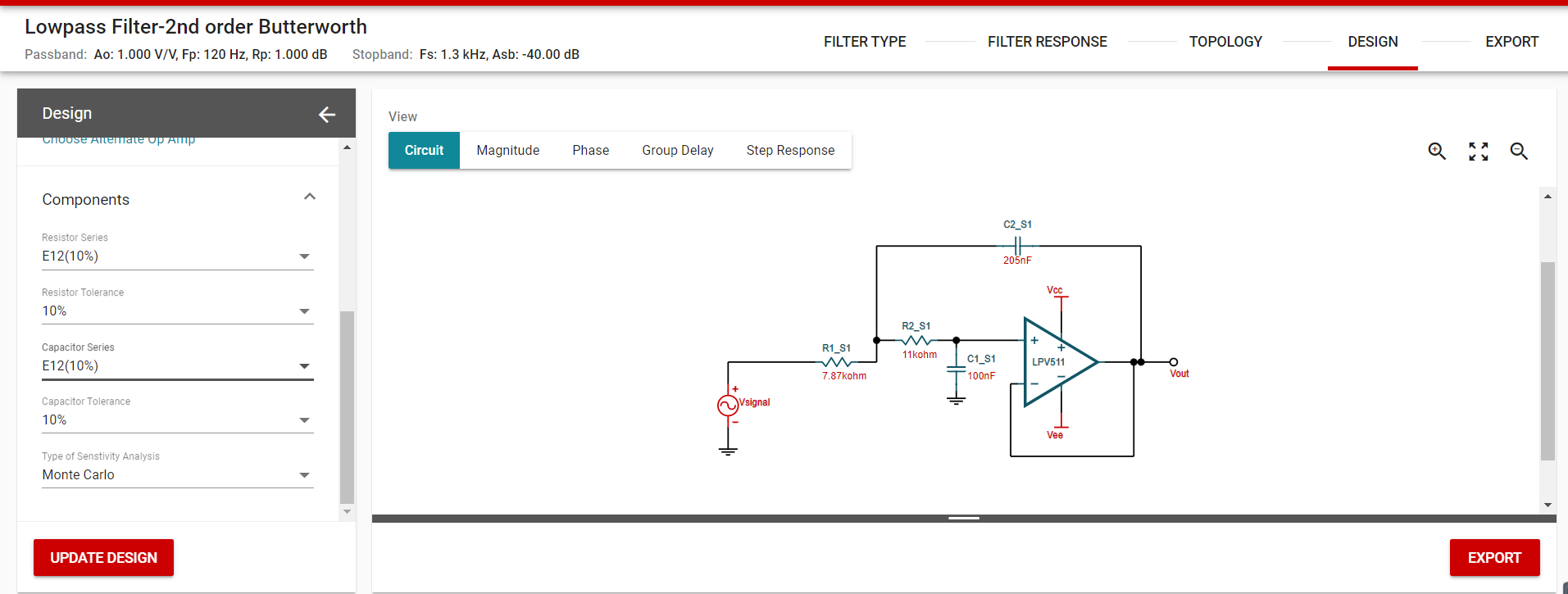
到这里一个有源滤波电路就完成了。
这个网页工具箱甚至还可以直接选择原件，然后下单。当然不需要的同学可以直接导出一个报告，你设计的这个滤波器的报告。
第二步：Multisim仿真验证这个滤波器
有了这样一个电路，下一步就是想办法去验证这个电路的可行性：
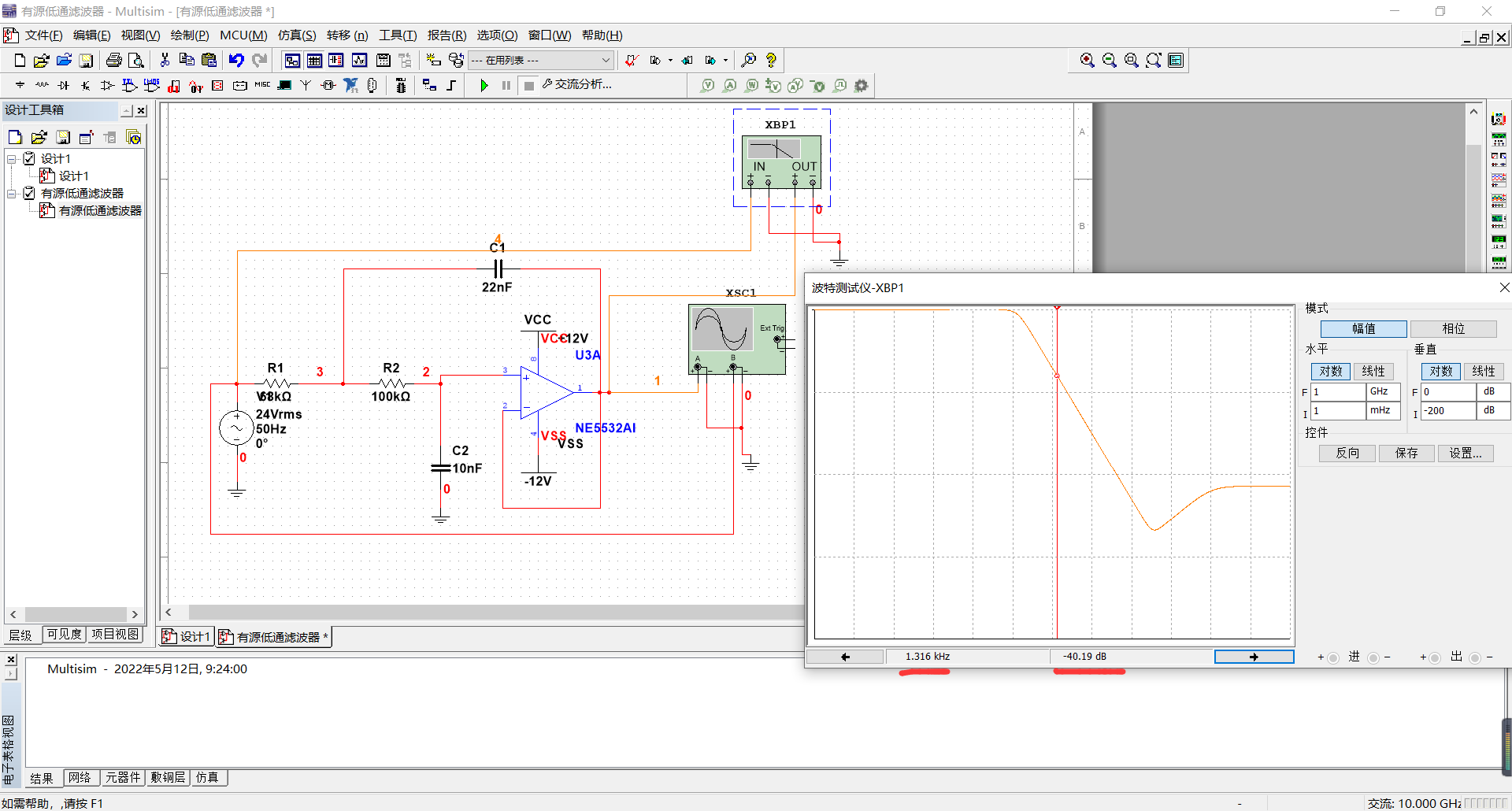
从上图可以很清楚的看到在1.3KHZ时，增益为-40dB。
当然这样还不够直观，这里我们使用两个信号发生器，一个50Hz的信号，一个1.3KHz，把这两个信号复合，再通过设计好的滤波器电路，查看效果。
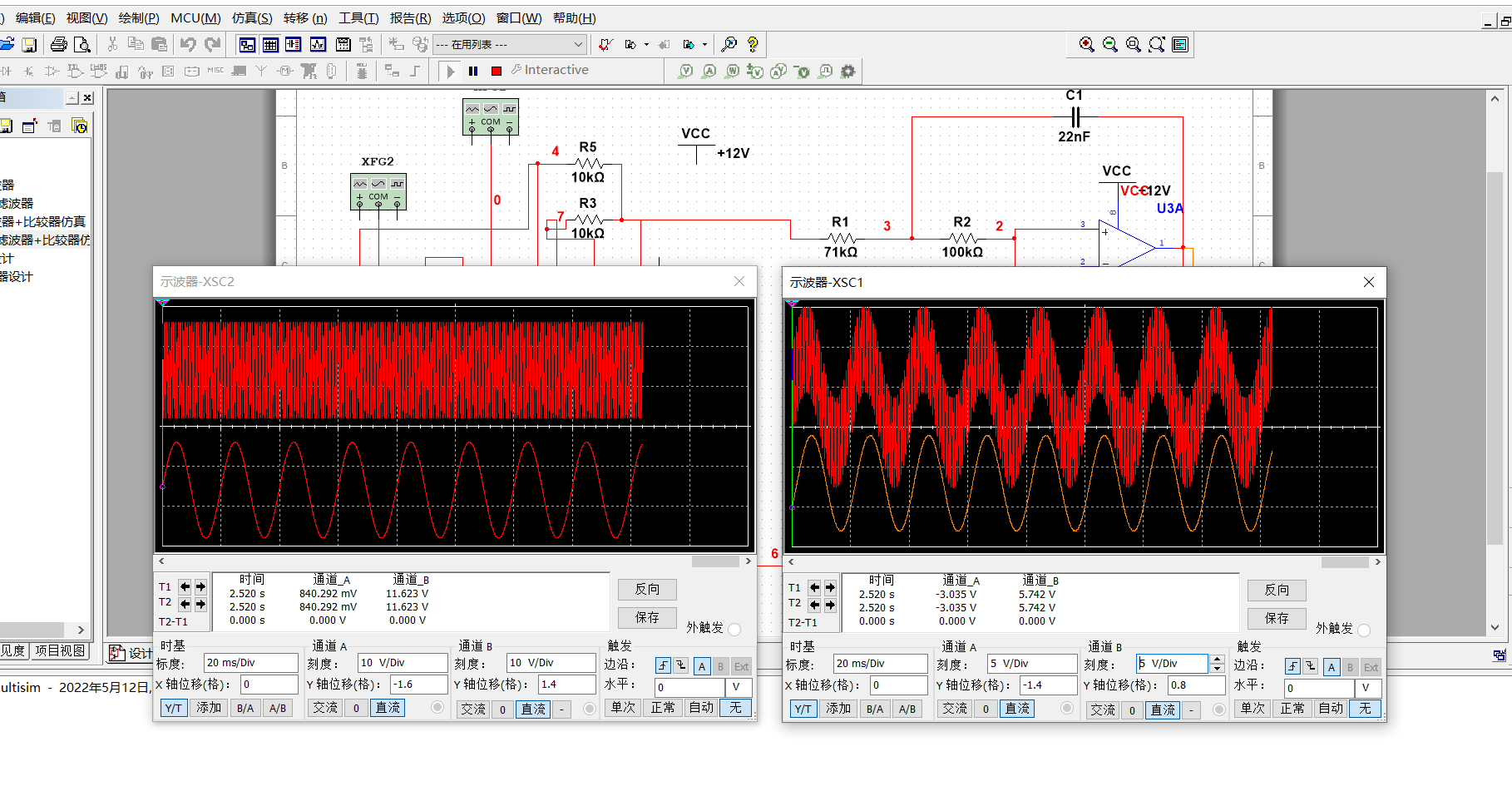
上面这个图的左边两个信号是两个信号发生器生成的信号，右边上面是两个信号复合之后的波形。
右边下面是滤除之后的波形，我们把输入的50Hz信号和最后得到的信号波信号放下一起比较：
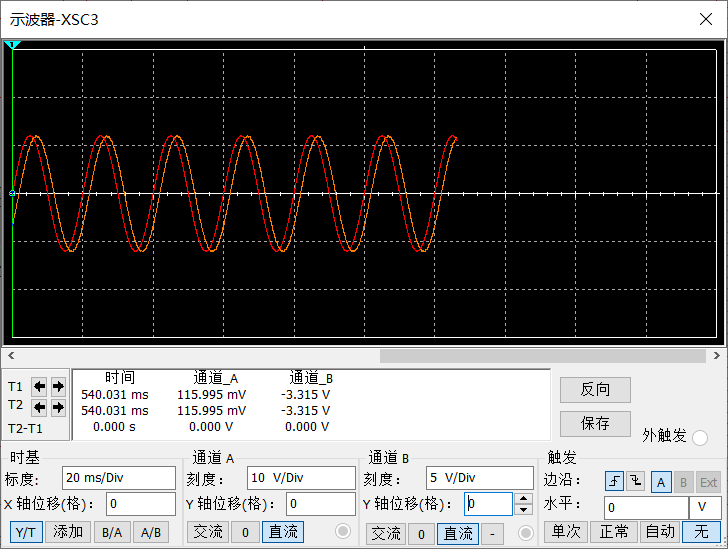
可见没有完全重合，因为经过滤波器之后是有一定时延的。
如果觉得还不够直观，我们可以进行FFT分析。把时域上的信号转移到频域上去观察。
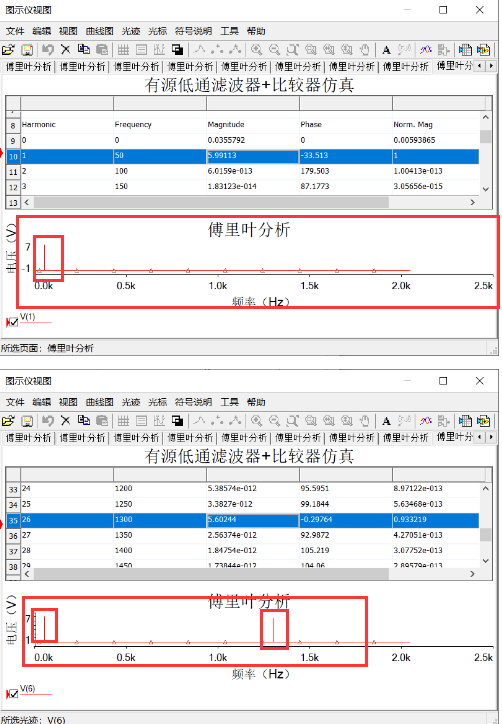
能够很明显的观察到，1.3KHz的信号已经被滤除并消失不见了。
经验证这个滤波器是完全没问题的。
如果说只是工程性的应用，到这一步其实就可以了。
但如果做的是理论分析，那就必不可少的需要的该滤波器的传递函数。
第三步：数学模型，公式推导
一开始我也是一步一步的去推这个公式。
但我们的目标是三分钟之内设计一款滤波器，很显然用手去推导是不行的。
所以这里给大家介绍几个Matlab的函数工具，求传递函数，只要几秒。
1.[N,wn]=buttord(wp,ws,rp,rs,'s') buttord函数
此函数的功能是根据数字滤波器的通带、阻带截止频率、通带衰减倍数、阻带衰减倍数来计算巴特沃斯数字滤波器的阶数N和3dB截止频率wn。
其中，调用参数wp，ws分别为数字滤波器的通带、阻带截止频率，
当ws≤wp时，为高通滤波器；当wp和ws为二元矢量时，为带通或带阻滤波器，这时w n 也是二元向量。rp，rs分别为通带最大衰减和组带最小衰减（dB）。
2.[B，A]=butter（N，wn，‘ftype’）butter 函数
此函数的功能是根据滤波器阶数N和截止频率wn计算N阶巴特沃斯数字滤波器系统函数分子、分母多项式的系数向量B、A。
其中，调用参数N和wn分别为巴特沃斯数字滤波器的阶数和3dB截止频率，
一般是可与buttord格式计算N和wn配合使用。系数B、A是按照z-1的升幂排列，ftype为滤波器的类型。N，wn为butter函数的调用参数。
3.buttap 函数 [Z，P，K] = buttap(N)
函数可设计出N阶巴特沃斯低通滤波器的零、极点。
实际演示：用第二个函数设计一个低通的巴特沃兹滤波器。
其传递函数模型如下：
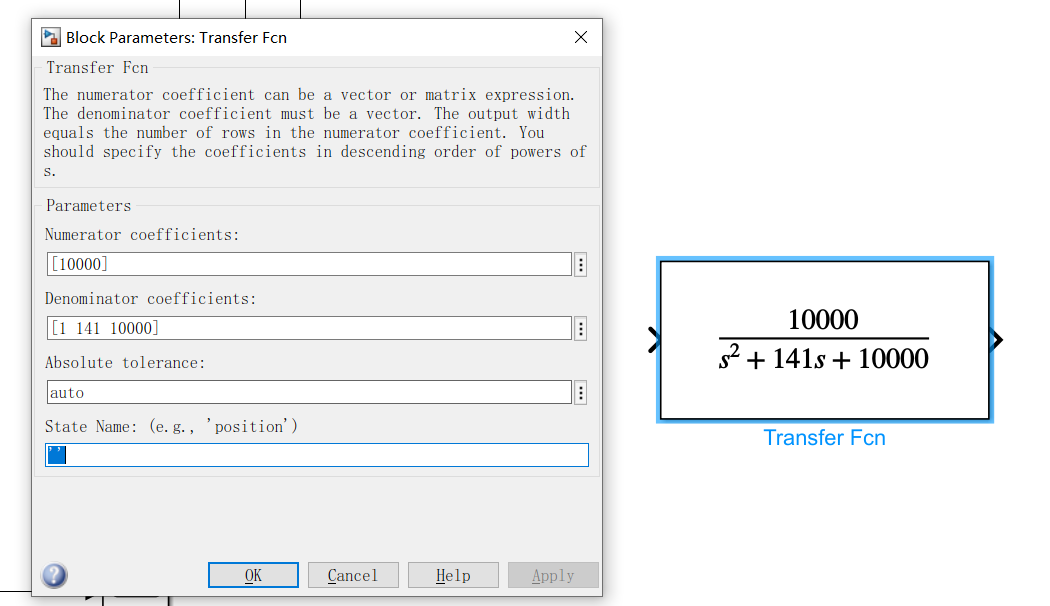
这样你就可以在simulink中与你的整个控制系统放在一起进行仿真。
仿真效果如下：
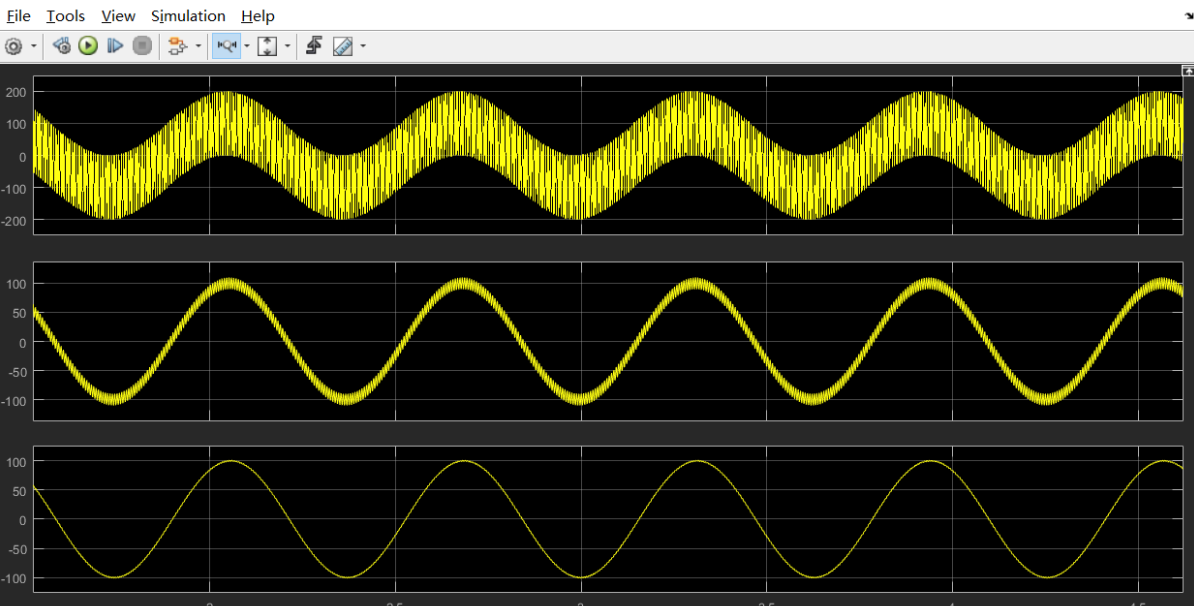
甚至你还可以直接绘制这个滤波器的幅频特性曲线：
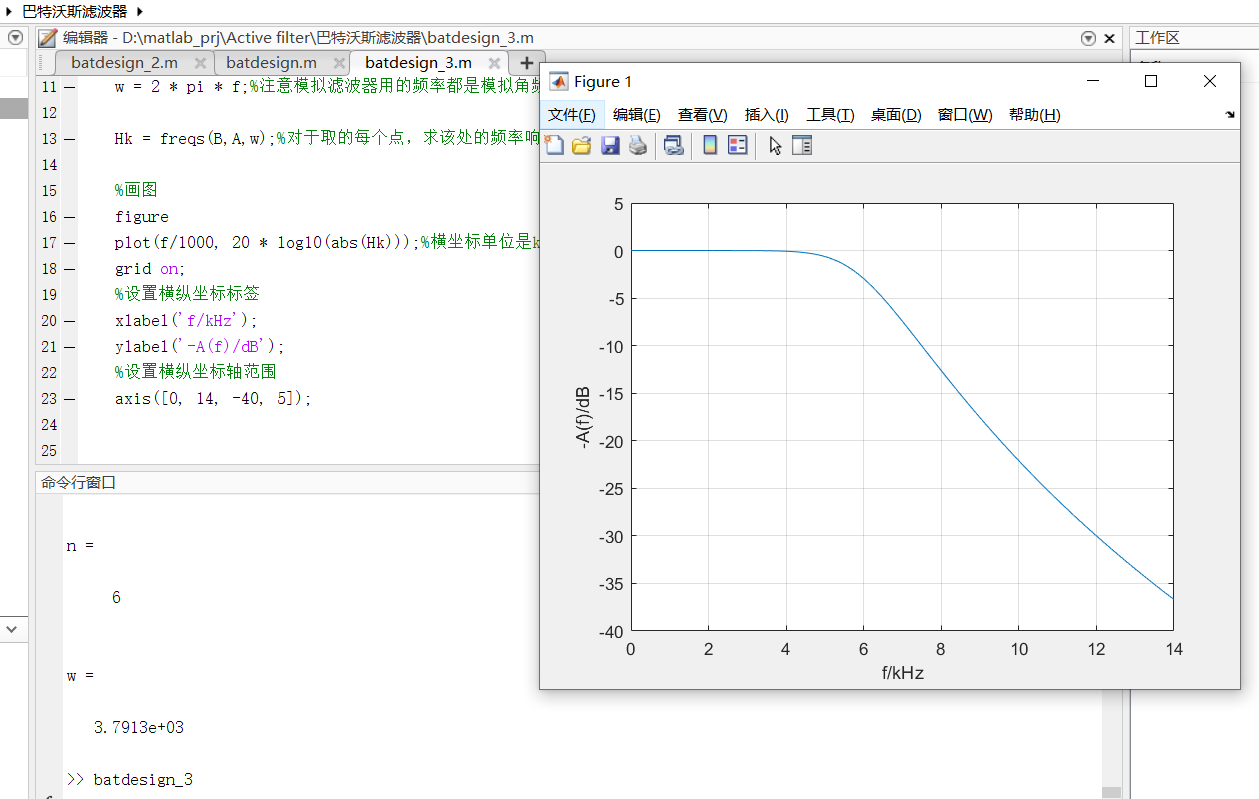
到此为止一个完整的设计闭环已经结束。
写在最后
写这个博文一方面给大家分享滤波器设计流程之外，还有一点就是强调工具的使用。
有很多轮子早已经被造好了，我们最为后来者，要善于去使用这些轮子，而不是去重复的造轮子。
最后祝大家早晚，午安和晚安！
（学校新政策，一周可以申请一次离校，指定时间前必须回来，真就跟监狱放风似的，不说了，我去放风了，拜拜~）
