基本算法

1.二分查找算法模板：

二分模板一共有两个，分别适用于不同情况。 算法思路：假设目标值在闭区间[l, r]中， 每次将区间长度缩小一半，当l = r时，我们就找到了目标值。

版本1

当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid + 1;，计算mid时不需要加1。

代码：

int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

版本2

当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid;，此时为了防止死循环，计算mid时需要加1。

代码：

int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

2.树状数组

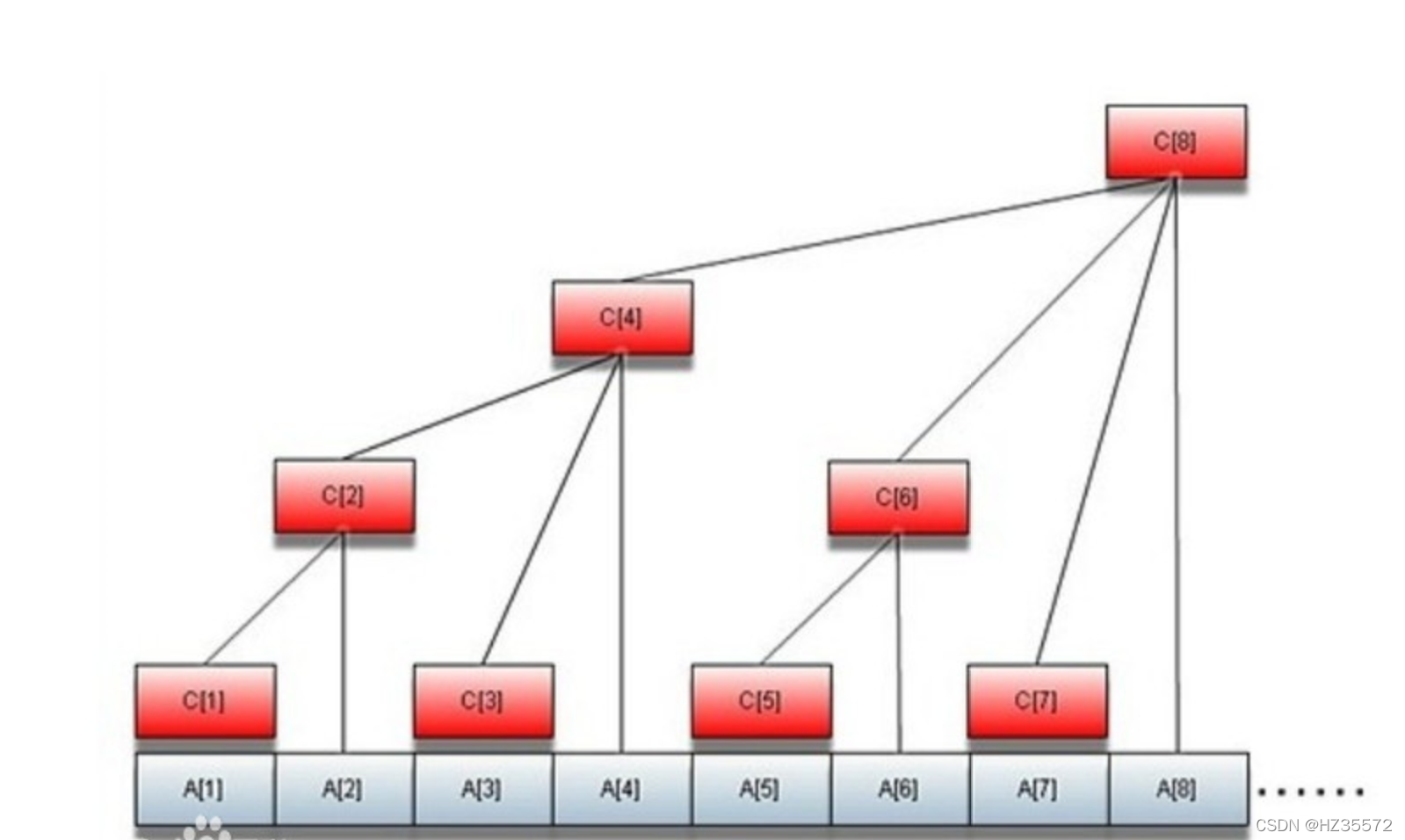
解释：

上图中:
C[1] = A[1];
C[2] = A[1] + A[2];
C[3] = A[3];
C[4] = A[1] + A[2] + A[3] + A[4];
C[5] = A[5];
C[6] = A[5] + A[6];
C[7] = A[7];
C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
————————————————
版权声明：本文为CSDN博主「HZ35572」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_51699436/article/details/122645188

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
const ll mod=1e9+7;
typedef pair<double,double> P;

int n;
int A[N],c[N];//对应原数组和树状数组

int lowbit(int x){
    return x&(-x);
}

void updata(int i,int k){ //在i位置加上k（修改）
    while(i<=n){
        c[i]+=k;
        i+=lowbit(i);
    }
}

int getsum(int i){  //求前i项的和（查询）
    int res=0;
    while(i>0){
        res+=c[i];
        i-=lowbit(i);
    }
    return res;
}

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>A[i];
        updata(i,A[i]);//第i个位置加上A[i]；
    }
    cout<<getsum(3)<<endl;//求前三项的和
    updata(2,2);//把第二个元素加上2
    cout<<getsum(3)<<endl;
    cout<<getsum(4)-getsum(1)<<endl;//求区间2~4之间的和
    cout<<getsum(2)-getsum(1)<<endl;//求第二个元素的值
    return 0;
}