互不侵犯KING
题意：一个$n * n$的棋盘，有$k$个国王，问有几种摆放的情况？
思路：爆搜直接寄，状压DP，将一行的状态表示为二进制状态比如101001，1表示这个位置放国王，然后转化成10进制数字，状压DP的套路就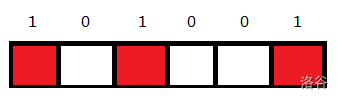
是不断枚举每个状态的数字，判断这种状态符不符合。
状态设置：
我们设置$ f[i][j][s]$ 表示我们选到第i行，第i行的状态为$S$ ,用了$j$个国王的方案数。
转移方程：
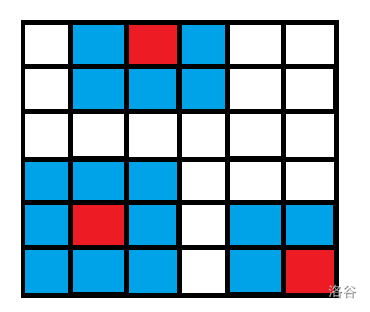红色表示国王，蓝色是攻击范围，当我们第i-1行的第j列有国王时，第i行有什么影响呢？
- 第i行的第j列，第j+1，j-1列都不能放了。我们用$S1$表示第i-1行的状态，$S2$表示i行的状态，那么就是当(S2&S1==0)&&((S2<<1)&S1)==0&&((S2>>1)&S1==0
- 第$i$行来说，那么就需要满足((S2<<1)&S2==0)&&((S2>>1)&S2==0);
然后考虑第二维的国王数是怎么转移的，对第i-1行来说，第i行多放的国王数就是第i行上的1的个数，我们用__builtin_popcount这个函数快速找到，那么转移方程式即是：$f[i][j][S2]$+=$f[i-1][j-cnt[S2]][S1]$
初始化细节提示：
$f[0][0][0]=1$，考虑1到（1<<n）这些状态下，哪些状态是满足条件二的，然后每次DP，枚举这些状态即可。
代码：
#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,k;
int f[10][100][1<<11];
int cnt[1<<11];
int st[1<<11];
//int king [1<<11],state[1<<11];
//int tot,ans;
//void init(){
// tot=(1<<n)-1;
// for (int i = 0; i <=tot ; ++i) {
// if(!((i<<1)&i)){
// state[++ans]=i;
// int t=i;
// while (t){
// king[ans]+=t%2,t>>=1;
// }
// }
// }
//}
int num;
void init(){
for (int s = 0; s <(1<<n) ; ++s) {
cnt[s]=__builtin_popcount(s);
if((((s<<1)|(s>>1))&s)==0) st[++num]=s;
}
}
void solve(){
cin>>n>>k;
init();
//当前的第i行，状态为S时，用了j个国王的方案数
f[0][0][0]=1;
for (int i = 1; i <=n ; ++i) {
for (int tem = 1; tem <=num ; ++tem) {
int s1=st[tem];
for (int last = 1; last <=num ; ++last) {
int s2=st[last];
if(((s2|(s2<<1)|(s2>>1))&s1)==0){
for (int j = 0; j <=k ; ++j) {
if(j-cnt[s1]>=0){
f[i][j][s1]+=f[i-1][j-cnt[s1]][s2];
}
}
}
}
}
}
// for(int i=1;i<=n;i++) //枚举我们已经放到了第几行
// {
// for(int l=1;l<=num;l++) //枚举第i行的状态,这里我们直接枚举所有满足条件2的状态,算是个优化吧
// {
// int s1=st[l];
// for(int r=1;r<=num;r++) //枚举上一行的状态
// {
// int s2=st[r];
// if(((s2|(s2<<1)|(s2>>1))&s1)==0) //如果上下,左下右上,左上右下方向都不相邻,合法
// {
// for(int j=0;j<=k;j++) //枚举国王个数
// if(j-cnt[s1]>=0)
// f[i][j][s1]+=f[i-1][j-cnt[s1]][s2]; //状态转移方程
// }
// }
// }
// }
int ans=0;
// cout<<num<<' ';
for (int i = 1; i <=num ; ++i) {
ans+=f[n][k][st[i]];
// cout<<f[n][k][st[i]]<<' ';
}
cout<<ans<<'\n';
}
signed main(){
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
int t=1;
//cin>>t;
while (t--)solve();
}
