solution-p4536

题解 P4536 【[CQOI2007]三角形】

原题

这是我们学校%你赛上的一道题。然而赛时只有70pts qwq。

首先显然可以得到当给出的三角形编号尾号为 \(4\) 时，仅有三个三角形与其相邻。

例如 \(\texttt{T4}\) 仅与 \(\texttt{T1,T2,T3}\) 相邻， \(\texttt{T24}\) 仅与 \(\texttt{T21,T22,T23}\) 相邻。

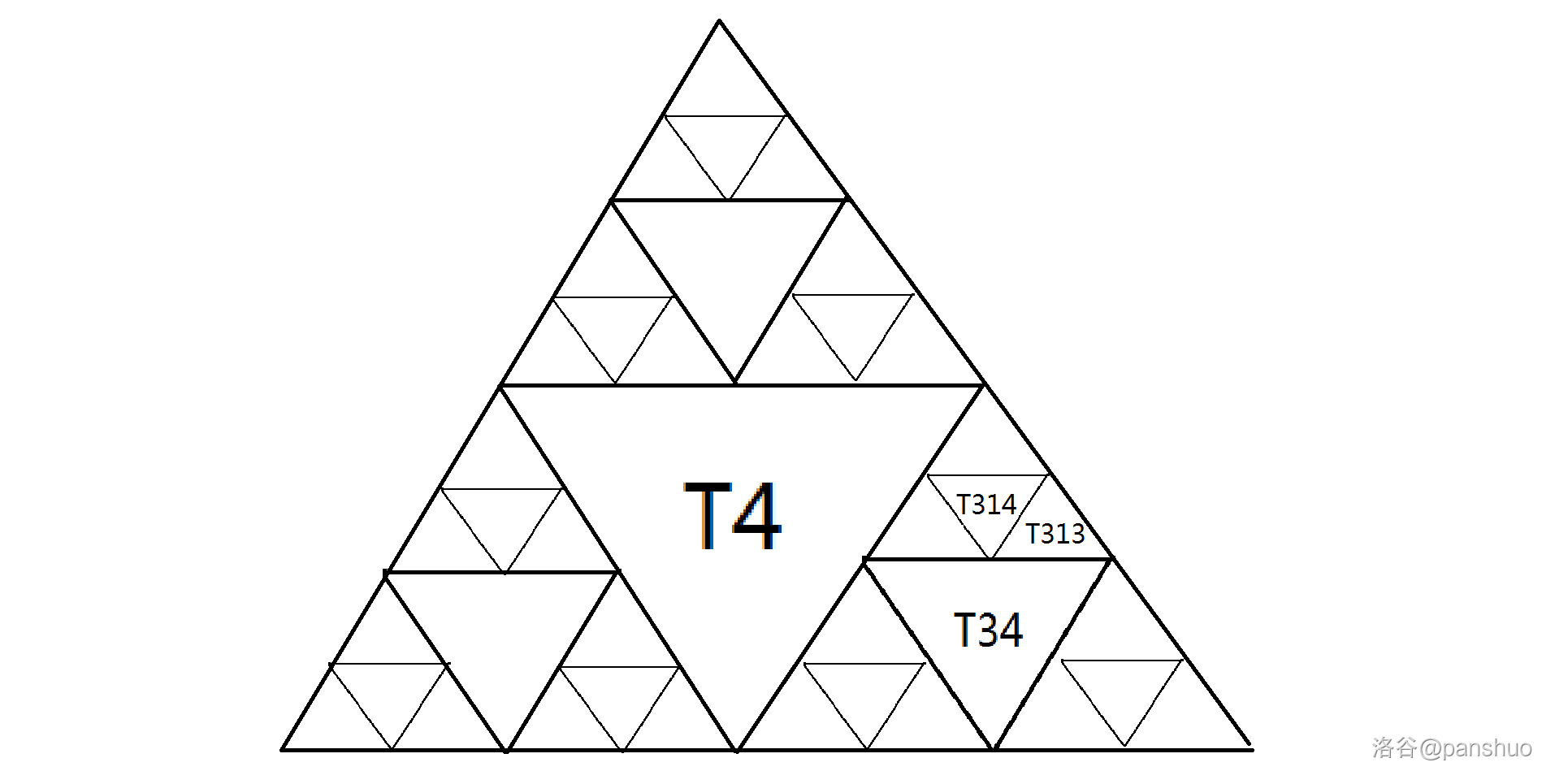
如果给出的三角形编号尾号不为 \(4\)，以 \(\texttt{T313}\)为例：

（这里为了方便说明，我们把尾号为 \(4\) 的三角形称为中央三角形；把同样大小且仅有尾号不同的三角形称为同级三角形。）

1. 首先 \(\texttt{T313}\) 必定与同级的中央三角形 \(T314\) 相邻。

2. 接着我们把 \(\texttt{T313}\) 放在大一点的三角形 \(\texttt{T31}\) 中看。可以得到 \(\texttt{T31}\) 必定与同级的中央三角形 \(\texttt{T34}\) 相邻，但是我们把 \(\texttt{T31}\) 进一步细分，就只有 \(\texttt{T312}\) 和 \(\texttt{T313}\) 两个三角形与 \(\texttt{T34}\) 相邻。所以 \(\texttt{T313}\) 与 \(\texttt{T34}\) 相邻。

3. 我们再把 \(\texttt{T313}\) 放在更大的三角形 \(\texttt{T3}\) 中看，虽然 \(\texttt{T3}\) 与 同级的中央三角形 \(\texttt{T4}\) 相邻，\(\texttt{T31}\) 也与 \(\texttt{T4}\) 相邻，但因为 \(\texttt{T313}\) 在 \(\texttt{T31}\) 的右下角，所以 \(\texttt{T313}\) 不会与 \(\texttt{T4}\) 相邻。

综上所述，我们可以得到结论：设\(|A|\) 表示三角形 \(A\) 的编号长度，\(A_i\) 表示 \(A\) 的第 \(i\) 位编号，则有：

原三角形 \(S\) 与一个中央三角形 \(T\) 相邻，当且仅当 \(S\) 所在的与 \(T\) 同级的中央三角形 \(N\) 满足 \(S_{|N|+1}\) 到 \(S_{|S|}\) 均不等于 \(N_{|N|}\)。

这个看起来挺绕的，但其实好好理解一下就可以发现这个结论很显然。

希望题解能帮助到大家。

代码

const int N = 1e2 + 10;
string s;
string ans[N];
int cnt,len;
int check(int k , char ch) // k -> |S| + 1,ch -> N|N|.
{
	for(int i = len - 1;i > k;i--) // 验证S|N| 到 S|S| 均不等于 N|N|
		if(s[i] == ch)
			return false;
	return true;
}
int main()
{
	cin >> s;
	len = s.size();
	if(s[len - 1] == '4')
	{
		ans[++cnt] = s; // 与原三角形仅有最后一位编号不同 
		ans[cnt][len - 1] = '1';
		ans[++cnt] = s;
		ans[cnt][len - 1] = '2';
		ans[++cnt] = s;
		ans[cnt][len - 1] = '3';
	}
	else
		for(int i = len - 1;i >= 1;i--) // 小三角形到大三角形地枚举，当然也可以正着枚举
			if( check( i , s[i] ) )
			{
				ans[++cnt] = s.substr(0 , i + 1); // T1 ~ Ti-1的编号是与原三角形相同的 
				ans[cnt][i] = '4'; // 同级的中央三角形 T. 
			}
	sort(ans + 1 , ans + cnt + 1); // string默认按字典序排序 
	for(int i = 1;i <= cnt;i++)
		cout << ans[i] << endl;
    return 0;
}