ANN key idea
神经网络的 key ideas
1、两种神经元
- 感知器、
- sigmoid 神经元
如今,用的更多的是其他神经元模型(sigmoid神经元),而不是感知器;要了解sigmoid神经元需要先了解感知器。
1.1 感知器
一个感知器有若干二值的输入,一个二值的输出。
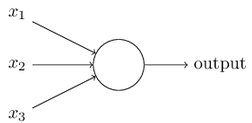
\(output = \left\{ \begin{array}{ll} 0 & \mbox{if } w\cdot x + b \leq 0 \\ 1 & \mbox{if } w\cdot x + b > 0 \end{array} \right.\)
1.2 为什么要用sigmoid神经元
- how learning work:
To see how learning might work, suppose we make a small change in some weight (or bias) in the network. What we'd like is for this small change in weight to cause only a small corresponding change in the output from the network. As we'll see in a moment, this property will make learning possible.
A small change in a weight (or bias) causes only a small change in output, then we could use this fact to modify the weights and biases to get our network to behave more in the manner we want.
Then we'd repeat this, changing the weights and biases over and over to produce better and better output. The network would be learning. - But, 感知器达不到上诉效果
But, the problem is that this isn't what happens when our network contains perceptrons. In fact, a small change in the weights or bias of any single perceptron in the network can sometimes cause the output of that perceptron to completely flip, say from 0 to 1.
That makes it difficult to see how to gradually modify the weights and biases so that the network gets closer to the desired behaviour. - 可以使用sigmoid神经元达到上诉效果
We can overcome this problem by introducing a new type of artificial neuron called a sigmoid neuron.
1.3 sigmoid神经元
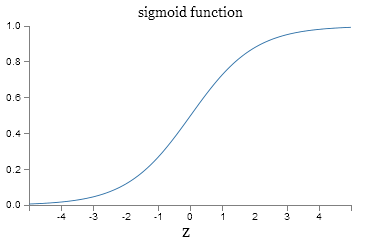
sigmoid function: \(\sigma(z)\equiv\frac{1}{1+e^{-z}}\)
sigmoid神经元输出为:\(output =\frac{1}{1+\exp(-\sum_j w_j x_j-b)}\)
笔记来源:Neural Networks and Deep Learning | Chapter 1
2、网络结构

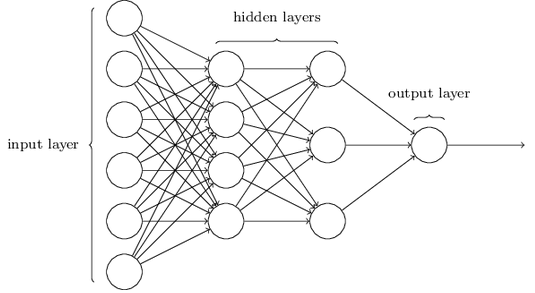
输入层 , 隐藏层(hidden layer),输出层
The term "hidden" perhaps sounds a little mysterious - the first time I heard the term I thought it must have some deep philosophical or mathematical significance - but it really means nothing more than "not an input or an output".
2.1 多层感知器
multilayer perceptrons or MLPs (for historical reasons)
2.2 输入输出层的设计
输入输出层的设计可以很简易,有几个输入就几个输入层;几个输出就几个输出层。
2.3 隐藏层的设计
隐藏层的设计有很多启发方法(后面介绍)
2.4 前馈、递归
feedforward neural networks (前馈型神经网络):output from one layer is used as input to the next layer.
This means there are no loops in the network - information is always fed forward, never fed back.
前面描述的都是前馈型神经网络。
recurrent neural networks (递归神经网络)
递归神经网络的学习能力没有 前馈型 强(至少目前);但是递归神经网络更接近人大脑的方式,而且有可能能解决那些 前馈型 很难解决的问题。(但本书主要关注广泛使用的前馈型神经网络)。
笔记来自:Neural Networks and Deep Learning | Chapter 1 | The architecture of neural networks
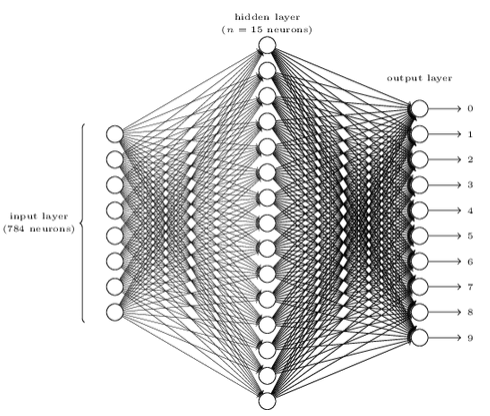
三层:输入(28*28),隐藏(15),输出(10).
输入:像素的灰度(01,白黑)
输出:为什么用10个输出,而不是4个(2^4=16>10)? 解释是:实际测试发现,10个输出的识别效果更好。但是为什么好?启发式的解释
笔记来自:Neural Networks and Deep Learning | Chapter 1 | A simple network to classify handwritten digits
Learning with gradient descent
输入向量:\(x\)
输出向量:\(y = y(x)\), \(y(x) = (0, 0, 0, 0, 0, 0, 1, 0, 0, 0)^T\)
cost function:\(C(w,b) \equiv\frac{1}{2n} \sum_x \| y(x) - a\|^2.\)
a:实际输出
笔记来自:Neural Networks and Deep Learning | Chapter 1 | Learning with gradient descent
接下来要写“简单手写数字分类”
What we'd like is an algorithm which lets us find weights and biases so that the output from the network approximates y(x) for all training inputs x.
我们需要一个算法让我们找到权重和biases。
So the aim of our training algorithm will be to minimize the cost C(w,b) as a function of the weights and biases.
\(C\) 由下面这样变化$ \Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 +
\frac{\partial C}{\partial v_2} \Delta v_2.
\tag{7}$
\(v\)的变化:\(\Delta v \equiv (\Delta v_1, \Delta v_2)^T\)
\(C\)的梯度:\(\nabla C \equiv \left( \frac{\partial C}{\partial v_1},
\frac{\partial C}{\partial v_2} \right)^T.
\tag{8}\)
\begin{eqnarray}
\Delta C \approx \nabla C \cdot \Delta v.
\tag{9}\end{eqnarray}
\(\nabla C\) 把\(v\)的变化与\(C\)的变化联系起来
当\(\Delta v = -\eta \nabla C, \tag{10}\) 即负梯度方向的时候,\(C\)一定下降



 浙公网安备 33010602011771号
浙公网安备 33010602011771号