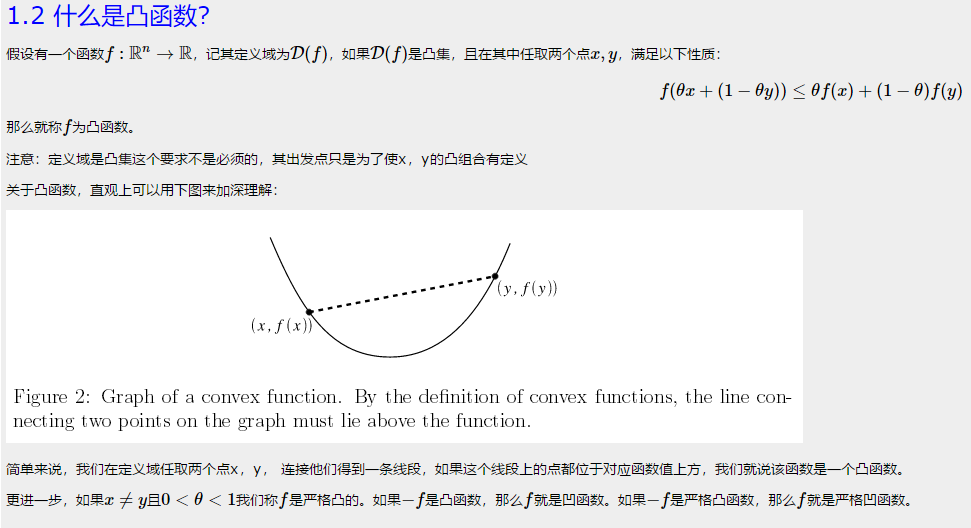
第一章 线性模型

---恢复内容开始---

 

   

 

 

 

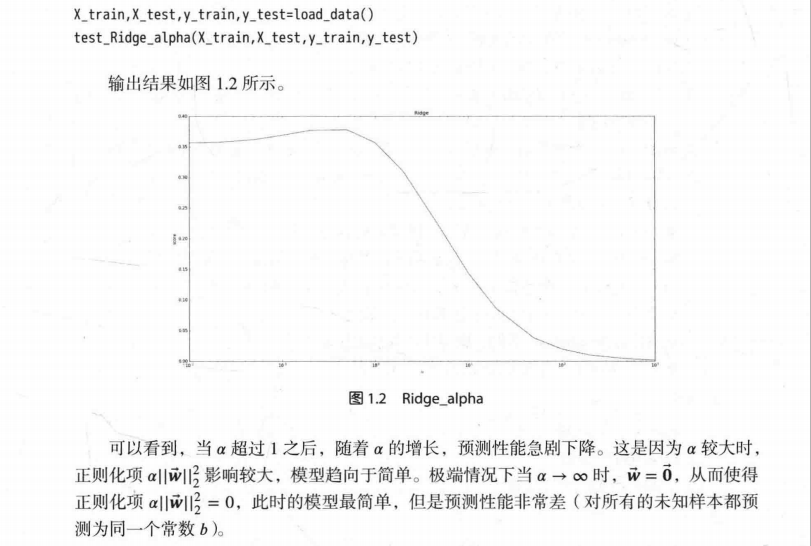
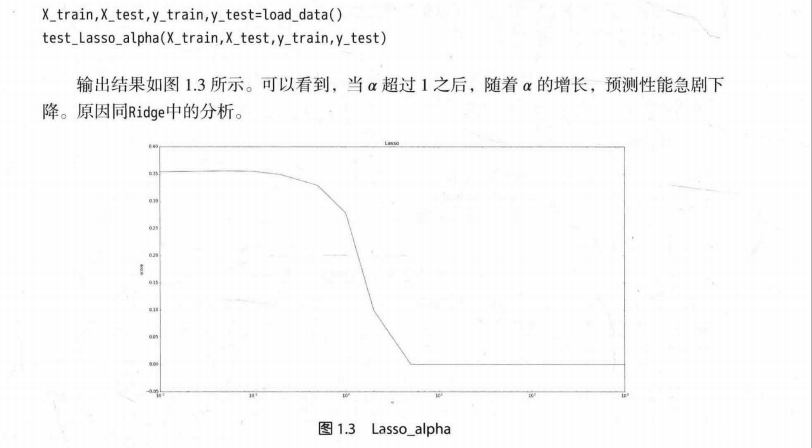
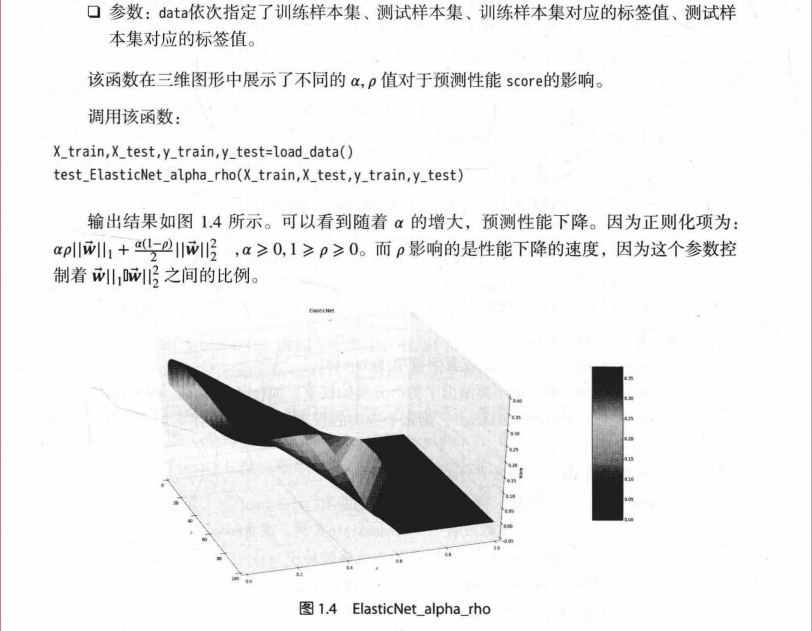
个人认为算法是错误的。

在for循环中

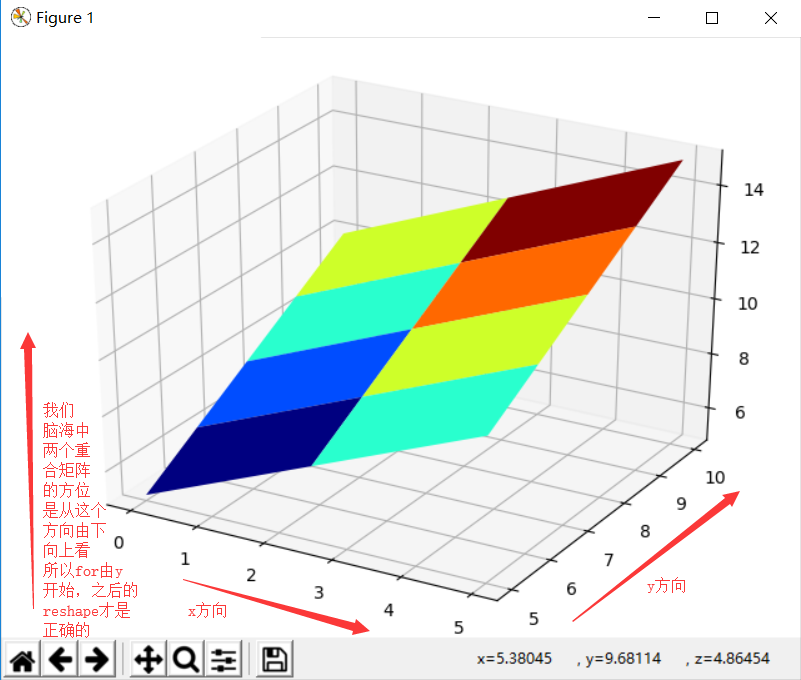
alpha与rho顺序反了，故后来的reshape操作是错的。

下面举个例子帮助理解：

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
fig = plt.figure()
ax = Axes3D(fig)

x = np.linspace(0, 5, 3)
y = np.linspace(5, 10, 5)
X, Y = np.meshgrid(x, y)  # XY平面的网格数据
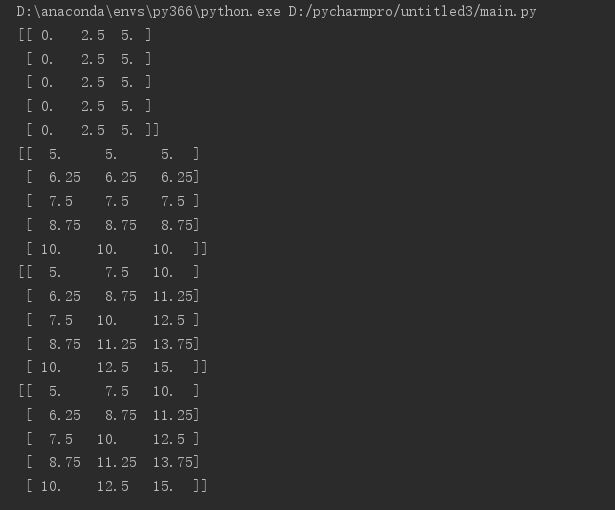
print(X)
print(Y)
Z=X+Y
print(Z)
Z=[]
#关键就在此处的for循环的顺序，另外XY肯定是（5，3）的，一定重合，想想一下这个重合的矩阵。但x轴的方向是X增大的方向，y轴方向是Y增大方向，
for aa in y:                          
    for bb in x:
        Z.append(aa+bb)
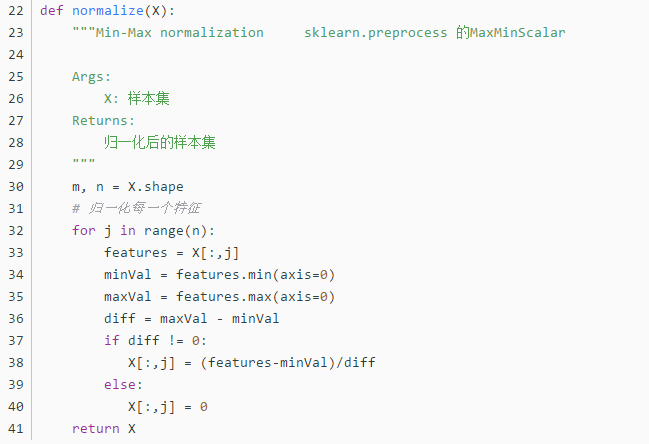
Z=np.array(Z).reshape(X.shape)
print(Z)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.jet)
# ax.plot_surface(X,Y,z,rstride=1,cstride=1,cmap=plt.get_cmap('rainbow'))
# 等高线图
ax.contourf(X, Y, Z, zdir='z', offset=-2, cmap='rainbow')  # zdir= x/y/x 轴的等高线 offset=等高线的位置

plt.show()

显示如下：

 

 

 

 

 

 

 

 

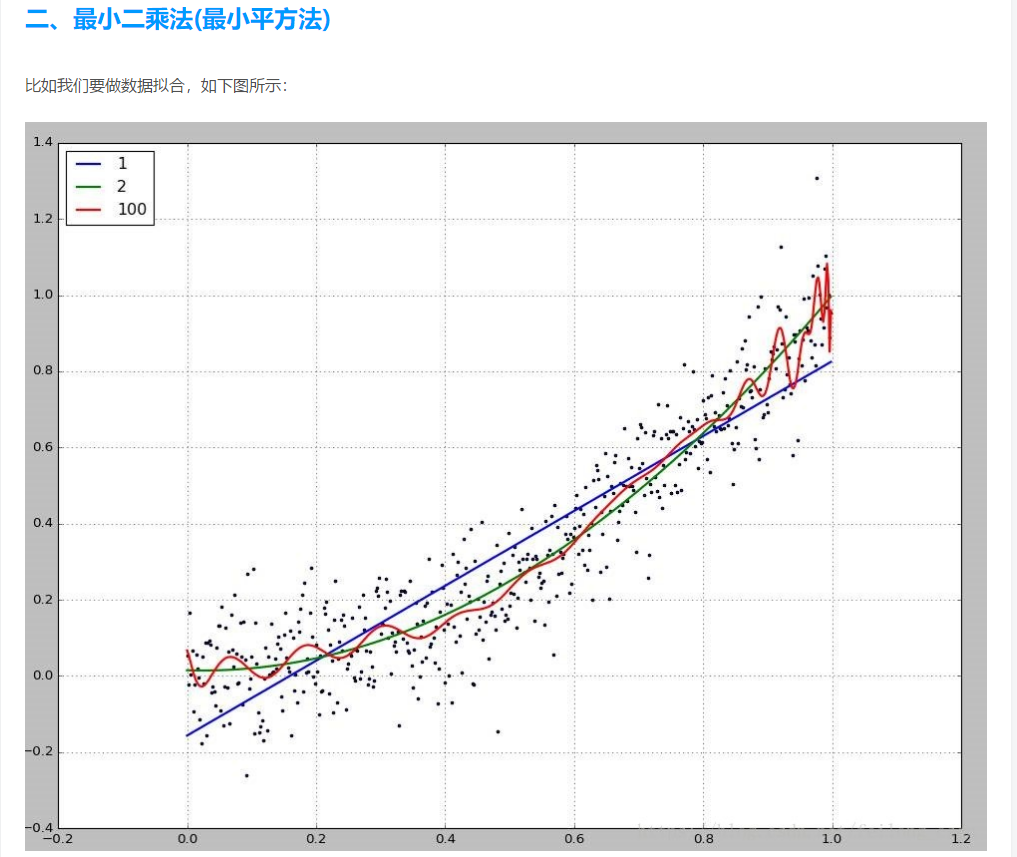
补充知识一：什么是最小二乘法

总结：

 

 一.背景

   5月9号到北大去听hulu的讲座《推荐系统和计算广告在视频行业应用》，想到能见到传说中的项亮大神，特地拿了本《推荐系统实践》求签名。讲座开始，主讲人先问了下哪些同学有机器学习的背景，我恬不知耻的毅然举手，真是惭愧。后来主讲人在讲座中提到了最小二乘法，说这个是机器学习最基础的算法。神马，最基础，我咋不知道呢！ 看来以后还是要对自己有清晰认识。

   回来赶紧上百度，搜了下什么是最小二乘法。

   先看下百度百科的介绍：最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

   通过这段描述可以看出来，最小二乘法也是一种优化方法，求得目标函数的最优值。并且也可以用于曲线拟合，来解决回归问题。难怪《统计学习方法》中提到，回归学习最常用的损失函数是平方损失函数，在此情况下，回归问题可以著名的最小二乘法来解决。看来最小二乘法果然是机器学习领域做有名和有效的算法之一。

二. 最小二乘法

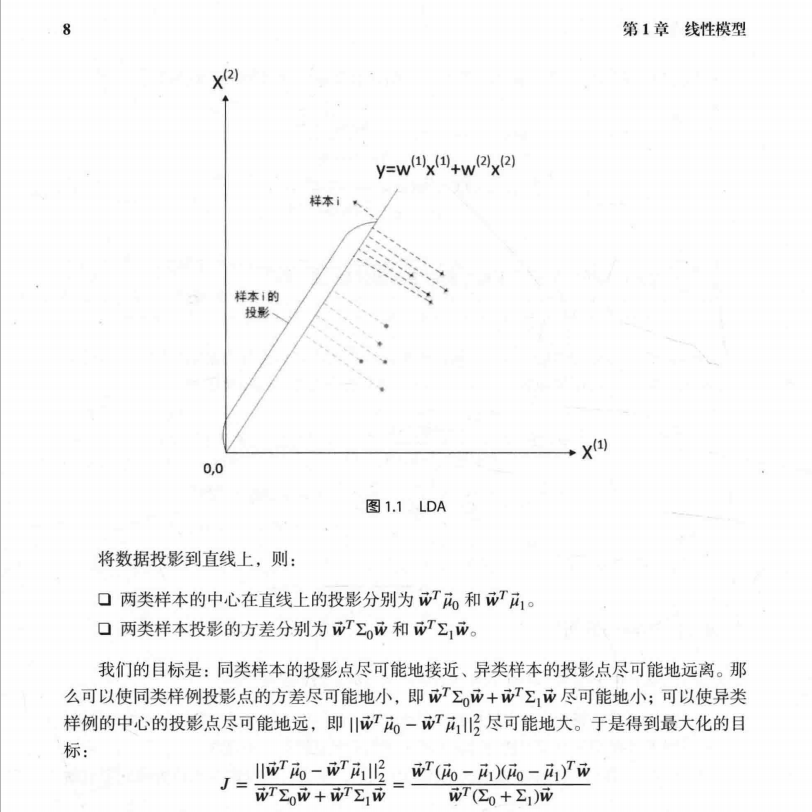
   我们以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢？ 监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。对于二维空间线性是一条直线；对于三维空间线性是一个平面，对于多维空间线性是一个超平面...

   对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：

        （1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
        （2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
        （3）最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。这种方法对异常值非常敏感。

　 最常用的是普通最小二乘法（ Ordinary  Least Square，OLS）：所选择的回归模型应该使所有观察值的残差平方和达到最小。（Q为残差平方和）- 即采用平方损失函数。

 　样本回归模型：

这就是最小二乘法的解法，就是求得平方损失函数的极值点。

 

 

 

 

 

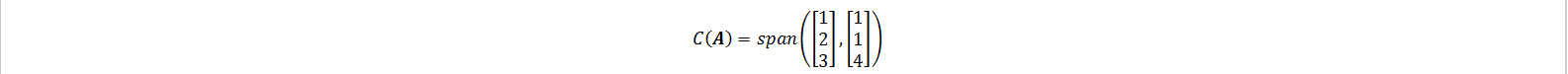
补充知识二：机器学习中 L1 和 L2 正则化的直观解释

机器学习中，如果参数过多，模型过于复杂，容易造成过拟合（overfit）。即模型在训练样本数据上表现的很好，但在实际测试样本上表现的较差，

不具备良好的泛化能力。为了避免过拟合，最常用的一种方法是使用使用正则化，例如 L1 和 L2 正则化。但是，正则化项是如何得来的？

其背后的数学原理是什么？L1 正则化和 L2 正则化之间有何区别？本文将给出直观的解释。

1. L2 正则化直观解释

L2 正则化公式非常简单，直接在原来的损失函数基础上加上权重参数的平方和：

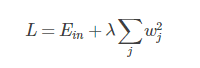
其中，Ein 是未包含正则化项的训练样本误差，λ 是正则化参数，可调。但是正则化项是如何推导的？接下来，我将详细介绍其中的物理意义。

我们知道，正则化的目的是限制参数过多或者过大，避免模型更加复杂。例如，使用多项式模型，如果使用 10 阶多项式，模型可能过于复杂，

容易发生过拟合。所以，为了防止过拟合，我们可以将其高阶部分的权重 w 限制为 0，这样，就相当于从高阶的形式转换为低阶。

为了达到这一目的，最直观的方法就是限制 w 的个数，但是这类条件属于 NP-hard 问题，求解非常困难。所以，一般的做法是寻找更宽松的限定条件：

上式是对 w 的平方和做数值上界限定，即所有w 的平方和不超过参数 C。这时候，我们的目标就转换为：最小化训练样本误差 Ein，但是要遵循 w 平方和小于 C 的条件。

下面，我用一张图来说明如何在限定条件下，对 Ein 进行最小化的优化。

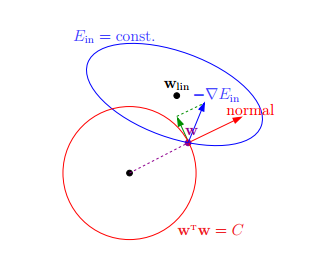
如上图所示，蓝色椭圆区域是最小化 Ein 区域，红色圆圈是 w 的限定条件区域。在没有限定条件的情况下，一般使用梯度下降算法，在蓝色椭圆区域内会一直沿着 w

梯度的反方向前进，直到找到全局最优值 wlin。例如空间中有一点 w（图中紫色点），此时 w 会沿着 -∇Ein 的方向移动，如图中蓝色箭头所示。但是，由于存在限定条件，

w 不能离开红色圆形区域，最多只能位于圆上边缘位置，沿着切线方向。w 的方向如图中红色箭头所示。

那么问题来了，存在限定条件，w 最终会在什么位置取得最优解呢？也就是说在满足限定条件的基础上，尽量让 Ein 最小。

我们来看，w 是沿着圆的切线方向运动，如上图绿色箭头所示。运动方向与 w 的方向（红色箭头方向）垂直。运动过程中，根据向量知识，只要 -∇Ein 与运行方向有夹角，

不垂直，则表明 -∇Ein 仍会在 w 切线方向上产生分量，那么 w 就会继续运动，寻找下一步最优解。只有当 -∇Ein 与 w 的切线方向垂直时，-∇Ein在 w 的切线方向才没有分量，

这时候 w 才会停止更新，到达最接近 wlin 的位置，且同时满足限定条件。

-∇Ein 与 w 的切线方向垂直，即 -∇Ein 与 w 的方向平行。如上图所示，蓝色箭头和红色箭头互相平行。这样，根据平行关系得到：

这样，我们就把优化目标和限定条件整合在一个式子中了。也就是说只要在优化 Ein 的过程中满足上式，就能实现正则化目标。

接下来，重点来了！根据最优化算法的思想：梯度为 0 的时候，函数取得最优值。已知 ∇Ein 是 Ein 的梯度，观察上式，λw 是否也能看成是某个表达式的梯度呢？

当然可以！λw 可以看成是 1/2λw*w 的梯度：

2. L1 正则化直观解释

L1 正则化公式也很简单，直接在原来的损失函数基础上加上权重参数的绝对值：

我仍然用一张图来说明如何在 L1 正则化下，对 Ein 进行最小化的优化。

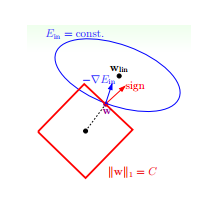
3. L1 与 L2 解的稀疏性

介绍完 L1 和 L2 正则化的物理解释和数学推导之后，我们再来看看它们解的分布性。

以二维情况讨论，上图左边是 L2 正则化，右边是 L1 正则化。从另一个方面来看，满足正则化条件，实际上是求解蓝色区域与黄色区域的交点，

即同时满足限定条件和 Ein 最小化。对于 L2 来说，限定区域是圆，这样，得到的解 w1 或 w2 为 0 的概率很小，很大概率是非零的。

对于 L1 来说，限定区域是正方形，方形与蓝色区域相交的交点是顶点的概率很大，这从视觉和常识上来看是很容易理解的。也就是说，

方形的凸点会更接近 Ein 最优解对应的 wlin 位置，而凸点处必有 w1 或 w2 为 0。这样，得到的解 w1 或 w2 为零的概率就很大了。所以，L1 正则化的解具有稀疏性。

扩展到高维，同样的道理，L2 的限定区域是平滑的，与中心点等距；而 L1 的限定区域是包含凸点的，尖锐的。这些凸点更接近 Ein 的最优解位置，而在这些凸点上，很多 wj 为 0。

关于 L1 更容易得到稀疏解的原因，有一个很棒的解释，请见下面的链接：

https://www.zhihu.com/question/37096933/answer/70507353

4. 正则化参数 λ

正则化是结构风险最小化的一种策略实现，能够有效降低过拟合。损失函数实际上包含了两个方面：一个是训练样本误差。一个是正则化项。其中，参数 λ 起到了权衡的作用。

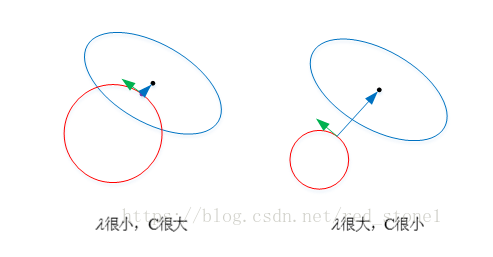
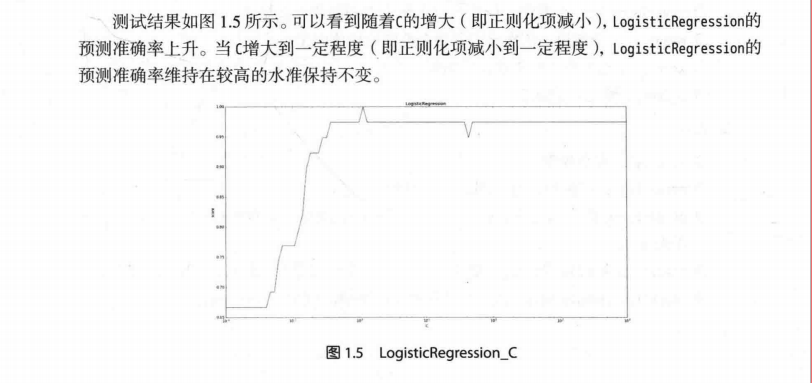
以 L2 为例，若 λ 很小，对应上文中的 C 值就很大。这时候，圆形区域很大，能够让 w 更接近 Ein 最优解的位置。若 λ 近似为 0，相当于圆形区域覆盖了最优解位置，这时候，正则化失效，容易造成过拟合。相反，若 λ 很大，对应上文中的 C 值就很小。这时候，圆形区域很小，w 离 Ein 最优解的位置较远。w 被限制在一个很小的区域内变化，w 普遍较小且接近 0，起到了正则化的效果。但是，λ 过大容易造成欠拟合。欠拟合和过拟合是两种对立的状态。
--------------------- 
作者：红色石头Will 
来源：CSDN 
原文：https://blog.csdn.net/red_stone1/article/details/80755144 

补充知识三：回归与分类的区别

笔记：分类与回归的区别在于输出变量的类型

           定量输出称为回归，或者说是连续变量预测

           定性输出称为分类，或者说是离散变量预测

           举个例子：

          预测明天的气温是多少度，是一个回归任务

          预测明天是阴，晴还是雨，是一个分类任务

补充知识四：什么是解析解，闭式解，数值解

多数函数解不出导数得0的解析解。梯度下降法是种数值算法，一般可以用计算机求出很好的近似解

补充知识点五：满秩矩阵

满秩矩阵

补充知识点六：归一化

一 引子

对房屋售价进行预测时，我们的特征仅有房屋面积一项，但是，在实际生活中，卧室数目也一定程度上影响了房屋售价。下面，我们有这样一组训练样本：

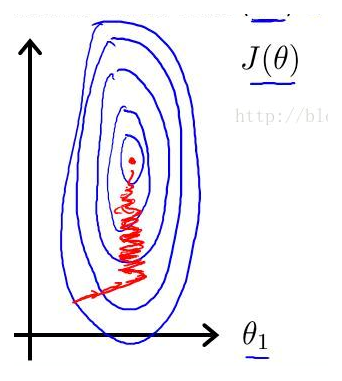
注意到，房屋面积及卧室数量两个特征在数值上差异巨大，如果直接将该样本送入训练，则代价函数的轮廓会是“扁长的”，在找到最优解前，梯度下降的过程

不仅是曲折的，也是非常耗时的：

 

 

二 归一化

     该问题的出现是因为我们没有同等程度的看待各个特征，即我们没有将各个特征量化到统一的区间。

     数据标准化（归一化）处理是数据挖掘的一项基础工作，不同评价指标往往具有不同的量纲和量纲单位，这样的情况会影响到数据分析的结果，

     为了消除指标之间的量纲影响，需要进行数据标准化处理，以解决数据指标之间的可比性。原始数据经过数据标准化处理后，各指标处于同一数量级，

     适合进行综合对比评价。以下是两种常用的归一化方法：

Standardization

          Standardization又称为Z-score normalization，量化后的特征将服从标准正态分布：

                   

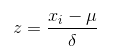
          其中，u和delta分别为对应特征的均值和标准差。量化后的特征将分布在[-1, 1]区间。

Min-Max Scaling

     Min-Max Scaling又称为Min-Max normalization， 特征量化的公式为：
                    

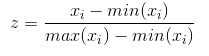
     量化后的特征将分布在[0,1]区间。

     大多数机器学习算法中，会选择Standardization来进行特征缩放，但是，Min-Max Scaling也并非会被弃置一地。

     在数字图像处理中，像素强度通常就会被量化到[0,1]区间，在一般的神经网络算法中，也会要求特征被量化[0，1]区间。

     进行了特征缩放以后，代价函数的轮廓会是“偏圆”的，梯度下降过程更加笔直，收敛更快性能因此也得到提升：

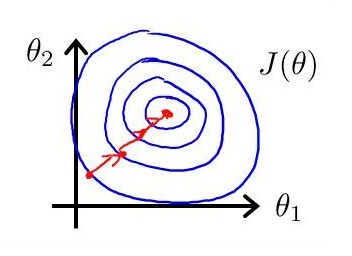
三 实现

     

     

 

--------------------- 
作者：一个人的场域 
来源：CSDN 
原文：https://blog.csdn.net/leiting_imecas/article/details/54986045

补充知识点七：scikit-learn 线性回归算法库小结

 

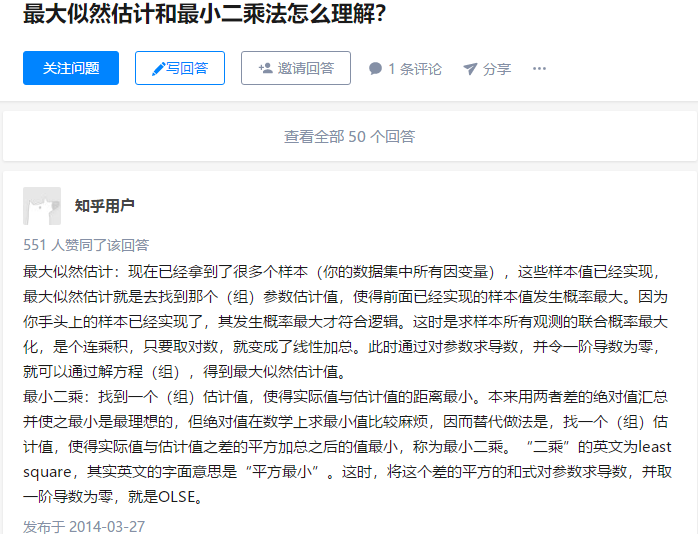
 补充知识点八：极大似然估计讲解

 

 

 

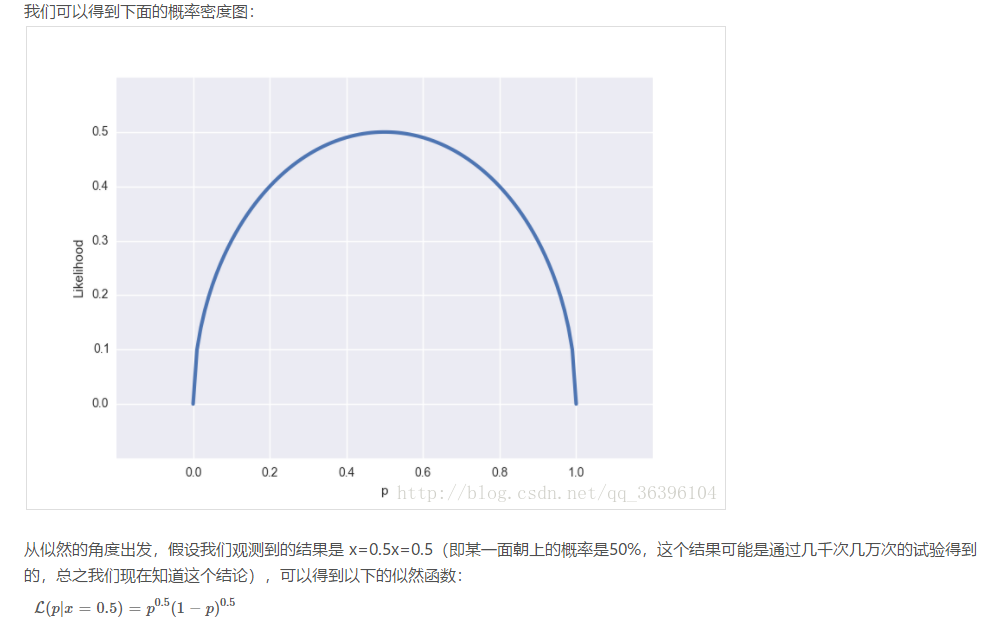
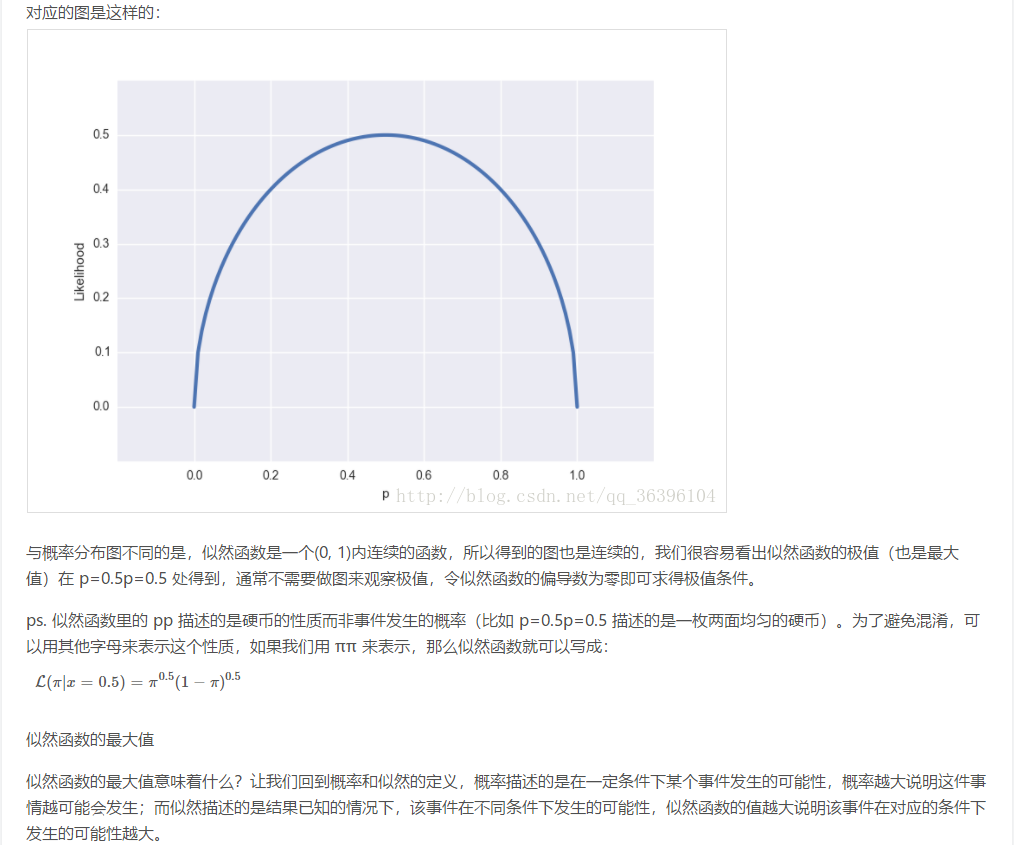
我们假设罐中白球的比例是p，那么黑球的比例就是1-p。因为每抽一个球出来，在记录颜色之后，我们把抽出的球放回了罐中并摇匀，所以每次抽出来的球的颜 色服从同一独立分布。这里我们把一次抽出来球的颜色称为一次抽样。题目中在一百次抽样中，七十次是白球的概率是P(Data | M)，这里Data是所有的数据，M是所给出的模型，表示每次抽出来的球是白色的概率为p。如果第一抽样的结果记为x1，第二抽样的结果记为x2... 那么Data = (x1,x2,…,x100)。这样，

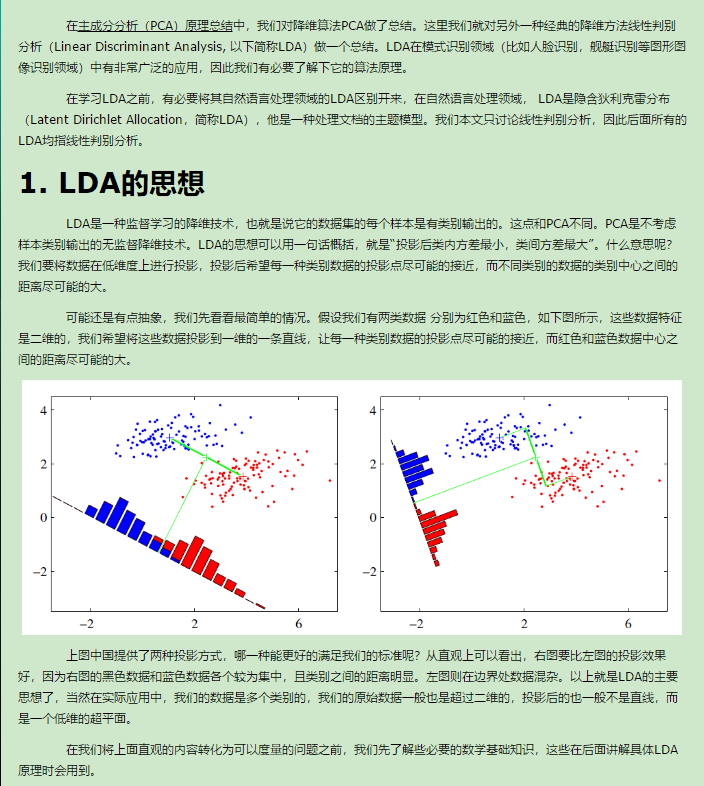
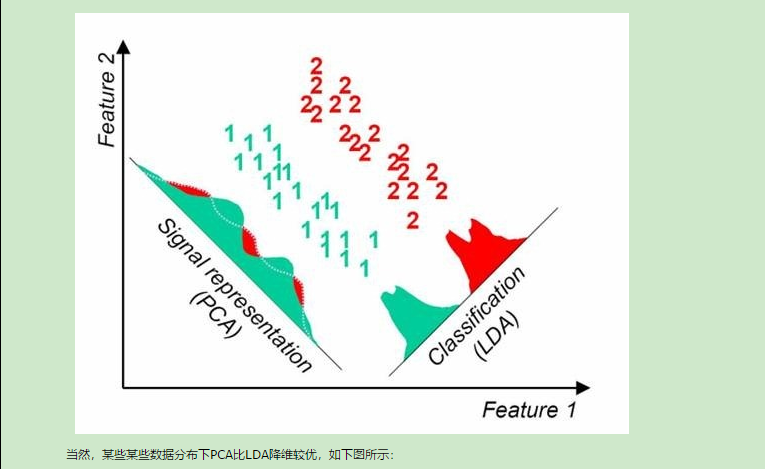
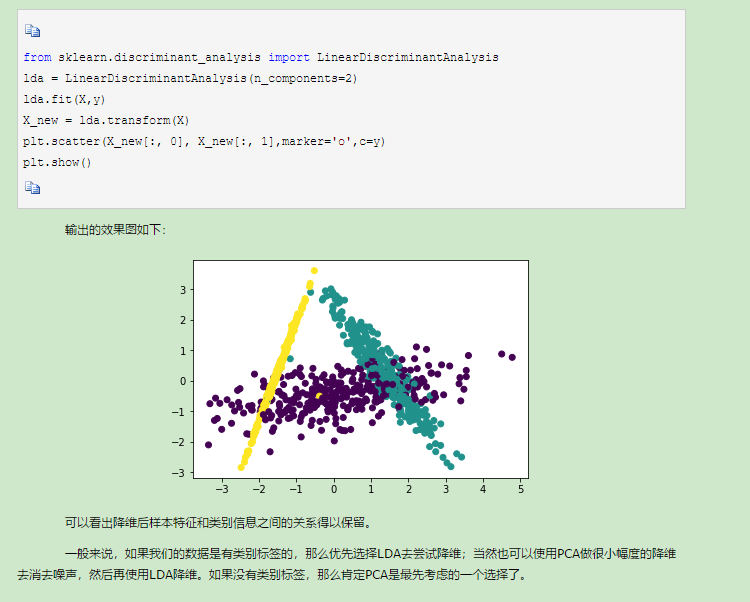
 补充知识点九：线性判别分析LDA原理总结

转自：http://www.cnblogs.com/pinard/p/6244265.html

 

 

补充知识点十：协方差矩阵

https://blog.csdn.net/shenziheng1/article/details/52955687

 

 

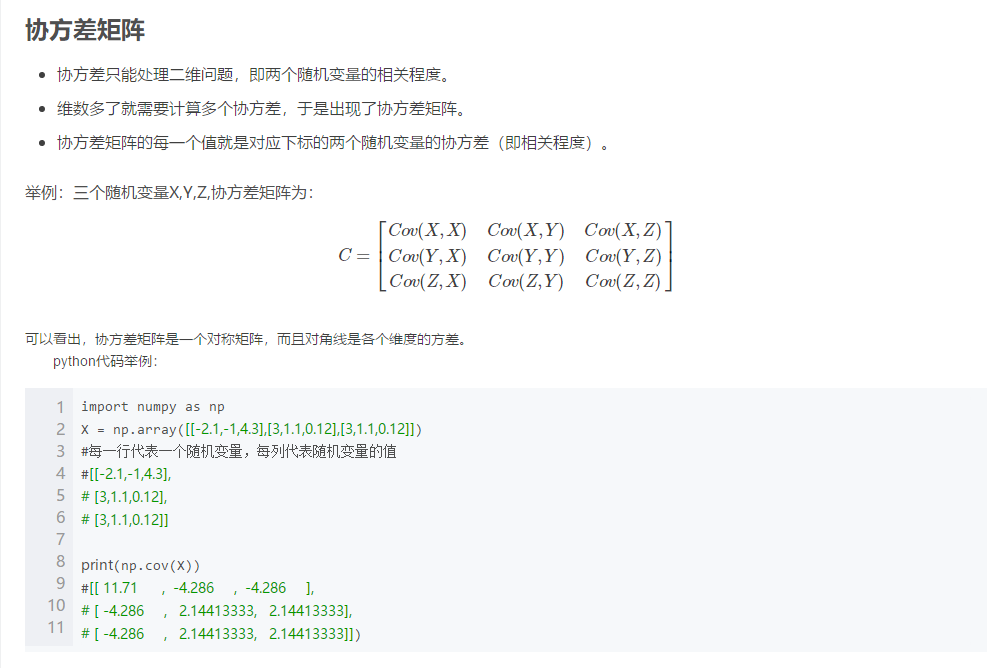
python里边列是样本

 

---恢复内容结束---

 

   

 

 

 

个人认为算法是错误的。

在for循环中

alpha与rho顺序反了，故后来的reshape操作是错的。

下面举个例子帮助理解：

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
fig = plt.figure()
ax = Axes3D(fig)

x = np.linspace(0, 5, 3)
y = np.linspace(5, 10, 5)
X, Y = np.meshgrid(x, y)  # XY平面的网格数据
print(X)
print(Y)
Z=X+Y
print(Z)
Z=[]
#关键就在此处的for循环的顺序，另外XY肯定是（5，3）的，一定重合，想想一下这个重合的矩阵。但x轴的方向是X增大的方向，y轴方向是Y增大方向，
for aa in y:                          
    for bb in x:
        Z.append(aa+bb)
Z=np.array(Z).reshape(X.shape)
print(Z)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.jet)
# ax.plot_surface(X,Y,z,rstride=1,cstride=1,cmap=plt.get_cmap('rainbow'))
# 等高线图
ax.contourf(X, Y, Z, zdir='z', offset=-2, cmap='rainbow')  # zdir= x/y/x 轴的等高线 offset=等高线的位置

plt.show()

显示如下：

 

 

 

 

 

 

 

 

补充知识一：什么是最小二乘法

 一.背景

   5月9号到北大去听hulu的讲座《推荐系统和计算广告在视频行业应用》，想到能见到传说中的项亮大神，特地拿了本《推荐系统实践》求签名。讲座开始，主讲人先问了下哪些同学有机器学习的背景，我恬不知耻的毅然举手，真是惭愧。后来主讲人在讲座中提到了最小二乘法，说这个是机器学习最基础的算法。神马，最基础，我咋不知道呢！ 看来以后还是要对自己有清晰认识。

   回来赶紧上百度，搜了下什么是最小二乘法。

   先看下百度百科的介绍：最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

   通过这段描述可以看出来，最小二乘法也是一种优化方法，求得目标函数的最优值。并且也可以用于曲线拟合，来解决回归问题。难怪《统计学习方法》中提到，回归学习最常用的损失函数是平方损失函数，在此情况下，回归问题可以著名的最小二乘法来解决。看来最小二乘法果然是机器学习领域做有名和有效的算法之一。

二. 最小二乘法

   我们以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢？ 监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。对于二维空间线性是一条直线；对于三维空间线性是一个平面，对于多维空间线性是一个超平面...

   对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：

        （1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
        （2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
        （3）最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。这种方法对异常值非常敏感。

　 最常用的是普通最小二乘法（ Ordinary  Least Square，OLS）：所选择的回归模型应该使所有观察值的残差平方和达到最小。（Q为残差平方和）- 即采用平方损失函数。

 　样本回归模型：

这就是最小二乘法的解法，就是求得平方损失函数的极值点。

 

补充知识二：机器学习中 L1 和 L2 正则化的直观解释

机器学习中，如果参数过多，模型过于复杂，容易造成过拟合（overfit）。即模型在训练样本数据上表现的很好，但在实际测试样本上表现的较差，

不具备良好的泛化能力。为了避免过拟合，最常用的一种方法是使用使用正则化，例如 L1 和 L2 正则化。但是，正则化项是如何得来的？

其背后的数学原理是什么？L1 正则化和 L2 正则化之间有何区别？本文将给出直观的解释。

1. L2 正则化直观解释

L2 正则化公式非常简单，直接在原来的损失函数基础上加上权重参数的平方和：

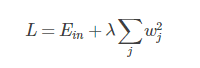
其中，Ein 是未包含正则化项的训练样本误差，λ 是正则化参数，可调。但是正则化项是如何推导的？接下来，我将详细介绍其中的物理意义。

我们知道，正则化的目的是限制参数过多或者过大，避免模型更加复杂。例如，使用多项式模型，如果使用 10 阶多项式，模型可能过于复杂，

容易发生过拟合。所以，为了防止过拟合，我们可以将其高阶部分的权重 w 限制为 0，这样，就相当于从高阶的形式转换为低阶。

为了达到这一目的，最直观的方法就是限制 w 的个数，但是这类条件属于 NP-hard 问题，求解非常困难。所以，一般的做法是寻找更宽松的限定条件：

上式是对 w 的平方和做数值上界限定，即所有w 的平方和不超过参数 C。这时候，我们的目标就转换为：最小化训练样本误差 Ein，但是要遵循 w 平方和小于 C 的条件。

下面，我用一张图来说明如何在限定条件下，对 Ein 进行最小化的优化。

如上图所示，蓝色椭圆区域是最小化 Ein 区域，红色圆圈是 w 的限定条件区域。在没有限定条件的情况下，一般使用梯度下降算法，在蓝色椭圆区域内会一直沿着 w

梯度的反方向前进，直到找到全局最优值 wlin。例如空间中有一点 w（图中紫色点），此时 w 会沿着 -∇Ein 的方向移动，如图中蓝色箭头所示。但是，由于存在限定条件，

w 不能离开红色圆形区域，最多只能位于圆上边缘位置，沿着切线方向。w 的方向如图中红色箭头所示。

那么问题来了，存在限定条件，w 最终会在什么位置取得最优解呢？也就是说在满足限定条件的基础上，尽量让 Ein 最小。

我们来看，w 是沿着圆的切线方向运动，如上图绿色箭头所示。运动方向与 w 的方向（红色箭头方向）垂直。运动过程中，根据向量知识，只要 -∇Ein 与运行方向有夹角，

不垂直，则表明 -∇Ein 仍会在 w 切线方向上产生分量，那么 w 就会继续运动，寻找下一步最优解。只有当 -∇Ein 与 w 的切线方向垂直时，-∇Ein在 w 的切线方向才没有分量，

这时候 w 才会停止更新，到达最接近 wlin 的位置，且同时满足限定条件。

-∇Ein 与 w 的切线方向垂直，即 -∇Ein 与 w 的方向平行。如上图所示，蓝色箭头和红色箭头互相平行。这样，根据平行关系得到：

这样，我们就把优化目标和限定条件整合在一个式子中了。也就是说只要在优化 Ein 的过程中满足上式，就能实现正则化目标。

接下来，重点来了！根据最优化算法的思想：梯度为 0 的时候，函数取得最优值。已知 ∇Ein 是 Ein 的梯度，观察上式，λw 是否也能看成是某个表达式的梯度呢？

当然可以！λw 可以看成是 1/2λw*w 的梯度：

2. L1 正则化直观解释

L1 正则化公式也很简单，直接在原来的损失函数基础上加上权重参数的绝对值：

我仍然用一张图来说明如何在 L1 正则化下，对 Ein 进行最小化的优化。

3. L1 与 L2 解的稀疏性

介绍完 L1 和 L2 正则化的物理解释和数学推导之后，我们再来看看它们解的分布性。

以二维情况讨论，上图左边是 L2 正则化，右边是 L1 正则化。从另一个方面来看，满足正则化条件，实际上是求解蓝色区域与黄色区域的交点，

即同时满足限定条件和 Ein 最小化。对于 L2 来说，限定区域是圆，这样，得到的解 w1 或 w2 为 0 的概率很小，很大概率是非零的。

对于 L1 来说，限定区域是正方形，方形与蓝色区域相交的交点是顶点的概率很大，这从视觉和常识上来看是很容易理解的。也就是说，

方形的凸点会更接近 Ein 最优解对应的 wlin 位置，而凸点处必有 w1 或 w2 为 0。这样，得到的解 w1 或 w2 为零的概率就很大了。所以，L1 正则化的解具有稀疏性。

扩展到高维，同样的道理，L2 的限定区域是平滑的，与中心点等距；而 L1 的限定区域是包含凸点的，尖锐的。这些凸点更接近 Ein 的最优解位置，而在这些凸点上，很多 wj 为 0。

关于 L1 更容易得到稀疏解的原因，有一个很棒的解释，请见下面的链接：

https://www.zhihu.com/question/37096933/answer/70507353

4. 正则化参数 λ

正则化是结构风险最小化的一种策略实现，能够有效降低过拟合。损失函数实际上包含了两个方面：一个是训练样本误差。一个是正则化项。其中，参数 λ 起到了权衡的作用。

以 L2 为例，若 λ 很小，对应上文中的 C 值就很大。这时候，圆形区域很大，能够让 w 更接近 Ein 最优解的位置。若 λ 近似为 0，相当于圆形区域覆盖了最优解位置，这时候，正则化失效，容易造成过拟合。相反，若 λ 很大，对应上文中的 C 值就很小。这时候，圆形区域很小，w 离 Ein 最优解的位置较远。w 被限制在一个很小的区域内变化，w 普遍较小且接近 0，起到了正则化的效果。但是，λ 过大容易造成欠拟合。欠拟合和过拟合是两种对立的状态。
--------------------- 
作者：红色石头Will 
来源：CSDN 
原文：https://blog.csdn.net/red_stone1/article/details/80755144 

补充知识三：回归与分类的区别

笔记：分类与回归的区别在于输出变量的类型

           定量输出称为回归，或者说是连续变量预测

           定性输出称为分类，或者说是离散变量预测

           举个例子：

          预测明天的气温是多少度，是一个回归任务

          预测明天是阴，晴还是雨，是一个分类任务

补充知识四：什么是解析解，闭式解，数值解

多数函数解不出导数得0的解析解。梯度下降法是种数值算法，一般可以用计算机求出很好的近似解

补充知识点五：满秩矩阵

满秩矩阵

补充知识点六：归一化

一 引子

对房屋售价进行预测时，我们的特征仅有房屋面积一项，但是，在实际生活中，卧室数目也一定程度上影响了房屋售价。下面，我们有这样一组训练样本：

注意到，房屋面积及卧室数量两个特征在数值上差异巨大，如果直接将该样本送入训练，则代价函数的轮廓会是“扁长的”，在找到最优解前，梯度下降的过程

不仅是曲折的，也是非常耗时的：

 

 

二 归一化

     该问题的出现是因为我们没有同等程度的看待各个特征，即我们没有将各个特征量化到统一的区间。

     数据标准化（归一化）处理是数据挖掘的一项基础工作，不同评价指标往往具有不同的量纲和量纲单位，这样的情况会影响到数据分析的结果，

     为了消除指标之间的量纲影响，需要进行数据标准化处理，以解决数据指标之间的可比性。原始数据经过数据标准化处理后，各指标处于同一数量级，

     适合进行综合对比评价。以下是两种常用的归一化方法：

Standardization

          Standardization又称为Z-score normalization，量化后的特征将服从标准正态分布：

                   

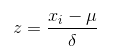
          其中，u和delta分别为对应特征的均值和标准差。量化后的特征将分布在[-1, 1]区间。

Min-Max Scaling

     Min-Max Scaling又称为Min-Max normalization， 特征量化的公式为：
                    

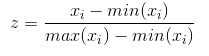
     量化后的特征将分布在[0,1]区间。

     大多数机器学习算法中，会选择Standardization来进行特征缩放，但是，Min-Max Scaling也并非会被弃置一地。

     在数字图像处理中，像素强度通常就会被量化到[0,1]区间，在一般的神经网络算法中，也会要求特征被量化[0，1]区间。

     进行了特征缩放以后，代价函数的轮廓会是“偏圆”的，梯度下降过程更加笔直，收敛更快性能因此也得到提升：

三 实现

     

     

 

--------------------- 
作者：一个人的场域 
来源：CSDN 
原文：https://blog.csdn.net/leiting_imecas/article/details/54986045

补充知识点七：scikit-learn 线性回归算法库小结

 

 补充知识点八：极大似然估计讲解

 

 

 

我们假设罐中白球的比例是p，那么黑球的比例就是1-p。因为每抽一个球出来，在记录颜色之后，我们把抽出的球放回了罐中并摇匀，所以每次抽出来的球的颜 色服从同一独立分布。这里我们把一次抽出来球的颜色称为一次抽样。题目中在一百次抽样中，七十次是白球的概率是P(Data | M)，这里Data是所有的数据，M是所给出的模型，表示每次抽出来的球是白色的概率为p。如果第一抽样的结果记为x1，第二抽样的结果记为x2... 那么Data = (x1,x2,…,x100)。这样，

 补充知识点九：线性判别分析LDA原理总结

转自：http://www.cnblogs.com/pinard/p/6244265.html

 

 

补充知识点十：协方差矩阵

https://blog.csdn.net/shenziheng1/article/details/52955687

 

 

python里边列是样本