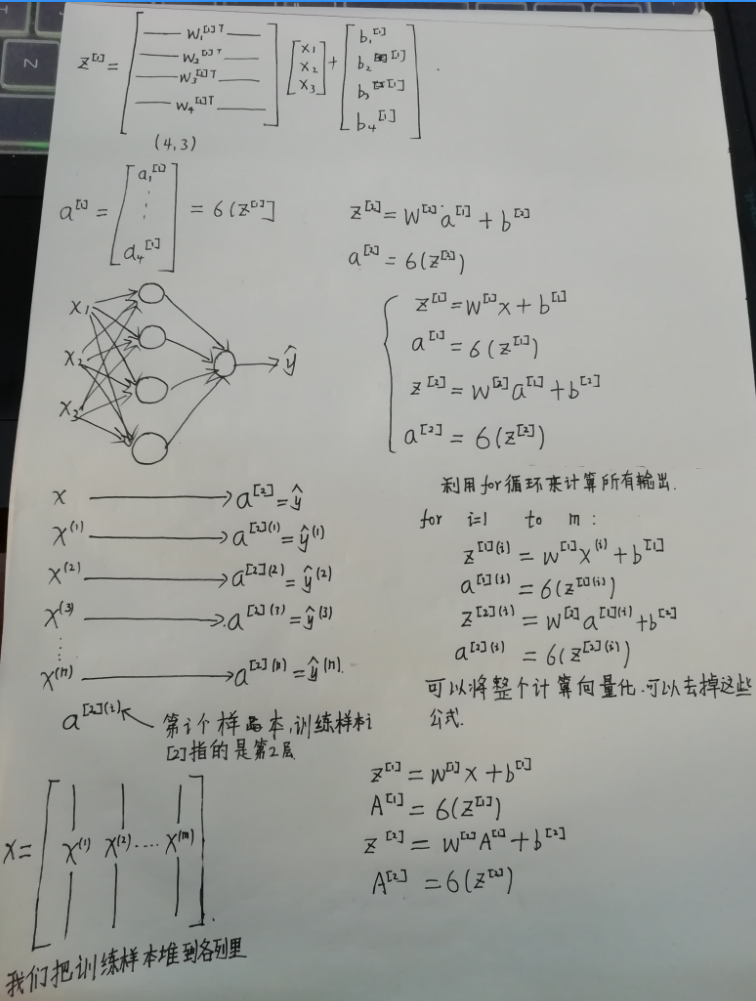
2.神经网络基础
深度学习就是训练神经网络
图像领域使用卷积神经网络cnn
对于序列数据(比如音频,语言,单词)使用循环神经网络rnn
结构化数据,每一列都有一个属性
非结构化数据,音频图像
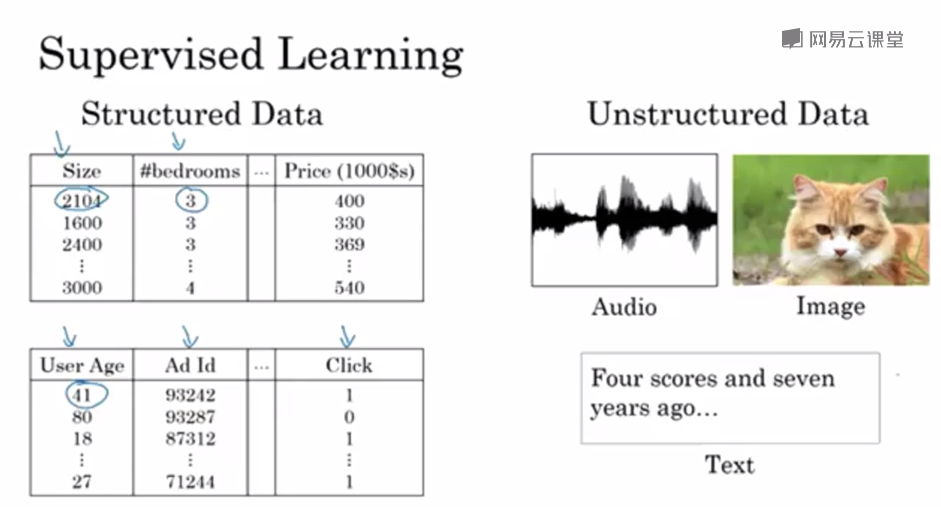

数据,计算能力,算法。算法的创新其实就是为了让计算能力更强
深度学习的一个大的转变就是由 sigmoid函数 转化到了 Relu函数。
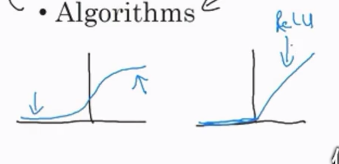
原因就是:sigmoid函数在箭头指的位置斜率为0,梯度为0,学习的非常缓慢,参数变得很慢。relu函数对所有正值的输入斜率都是1
logistic用于二分分类

j是凸函数
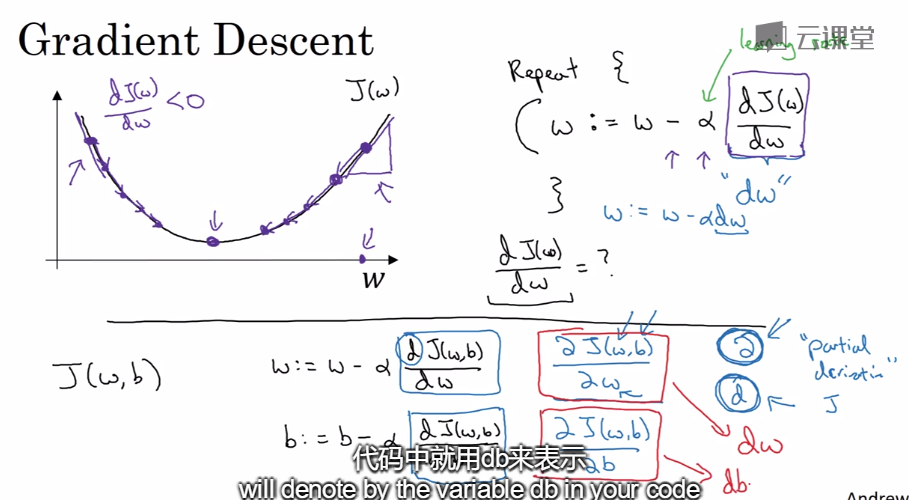
α是学习率









三年前,写过一篇逻辑回归算法的介绍,现在回头来看,比较乱,首尾不能兼顾。关于逻辑回归的分类算法,很多书籍都有介绍,比较来看,
还是李航老师的书《统计学习方法》里介绍的更清楚,若大家有时间,请不要偷懒,还是建议从头开始看李航老师的书,这本书简洁明了,适合入门。建议至少看1遍。
基于如上(主要参考李老师那本书),本篇博客,再次对逻辑回归,梳理如下,目的是让大家更快地理解逻辑回归。
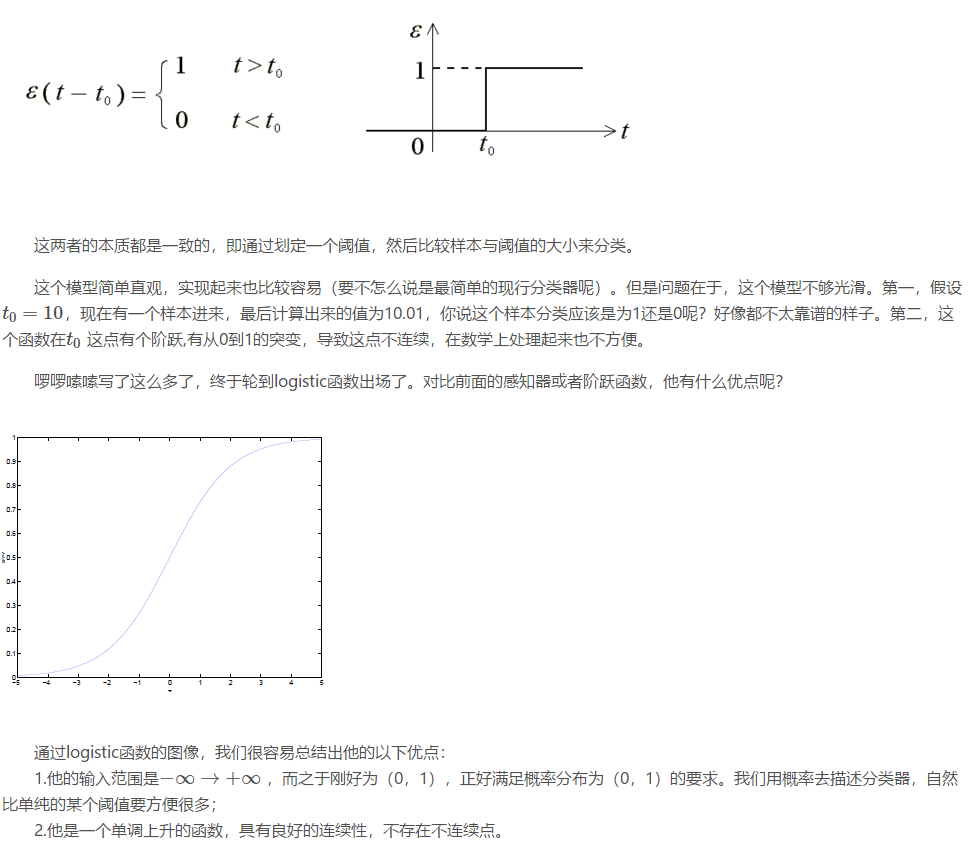
1. logistic分布的概念,如下图

logistic分布为什么常用呢?因为它的分布曲线,在中心附近增长很快,而在两端增长很慢。这就是说,若以概率0.5(中心点μ处的分布概率)为分界点,
大于μ的点Z为一类,小于μ的点为另一类,那么,我们能很好很快地把中心点附近的数据分类,就像越阶跳一样,不拖泥带水。
基于这个分布的特点,我们假设训练数据满足如下的模型:
2. Logistic回归的模型,如下图

3. Logistic模型中参数的求法(估计)
有了如上模型的假设,有了训练数据后,我们就可以把模型中的参数给求出来,具体方法如下:

4. 利用模型进行分类
利用3中的方法,得到一个logistic模型的结果如下:

则,对于测试数据或未来要分类的数据,我们只需把x带入上面的两个条件概率公式,哪个条件概率的值大,x对应的类别便是哪一类。

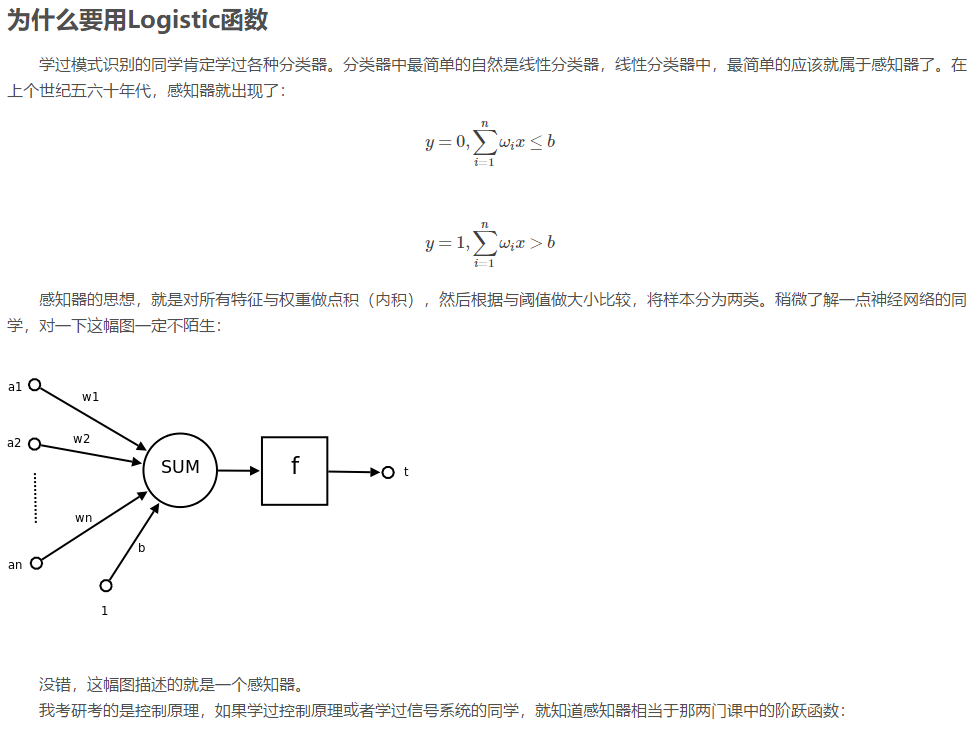

损失函数
损失函数一般指的是针对单个样本 i 做的损失,公式可以表示为:
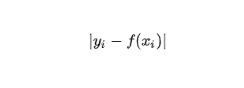
当然,只是举个例子,如果较真的话,还可以有交叉熵损失函数等。
成本函数
成本函数一般是数据集上总的成本函数,一般针对整体,根据上面的例子,这里的成本函数可以表示为:
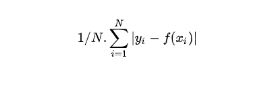
当然我们可以加上正则项
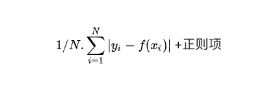


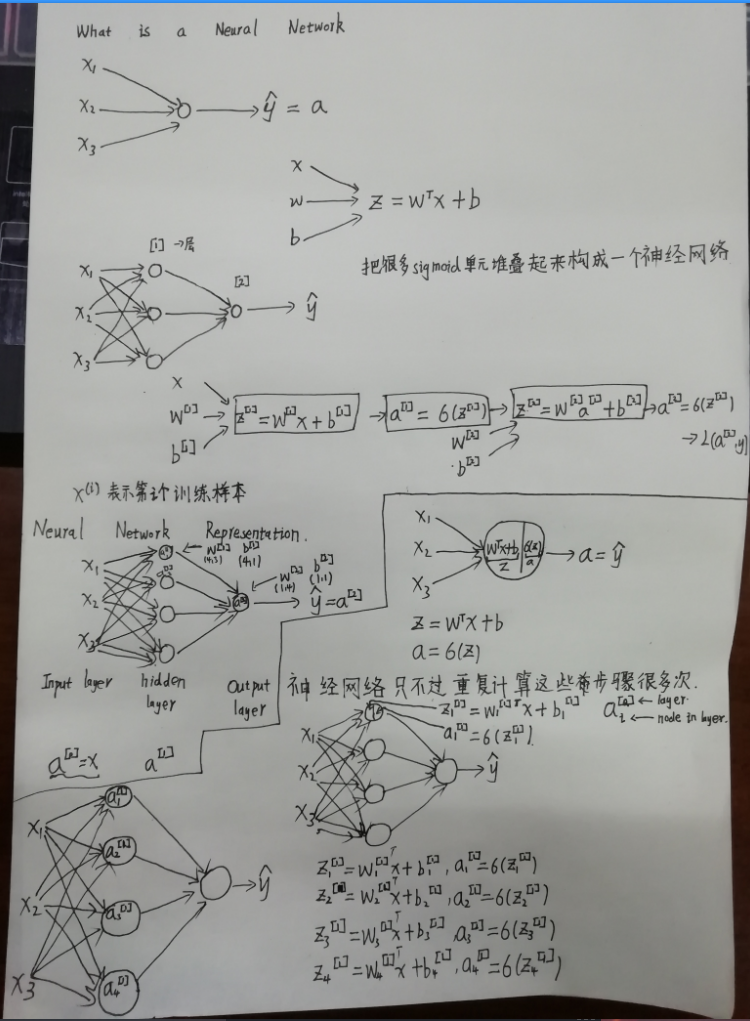
逻辑回归可以看作一个非常小的神经网络。
梯度下降算法“:







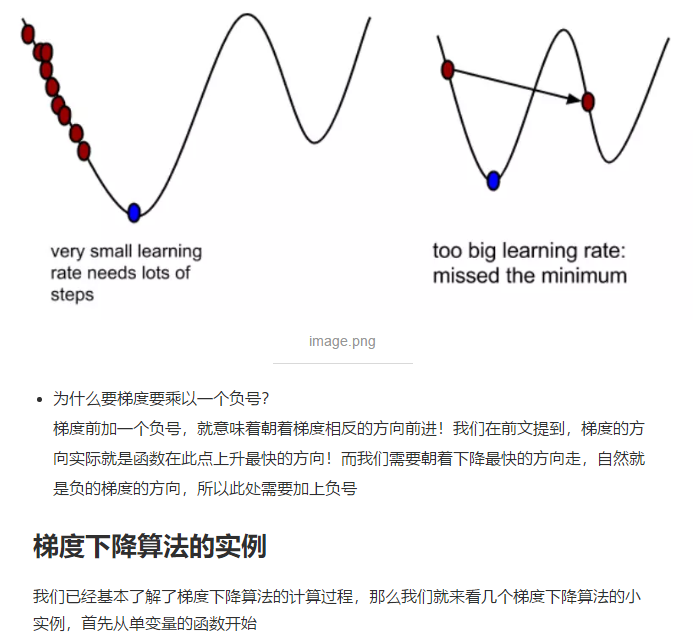


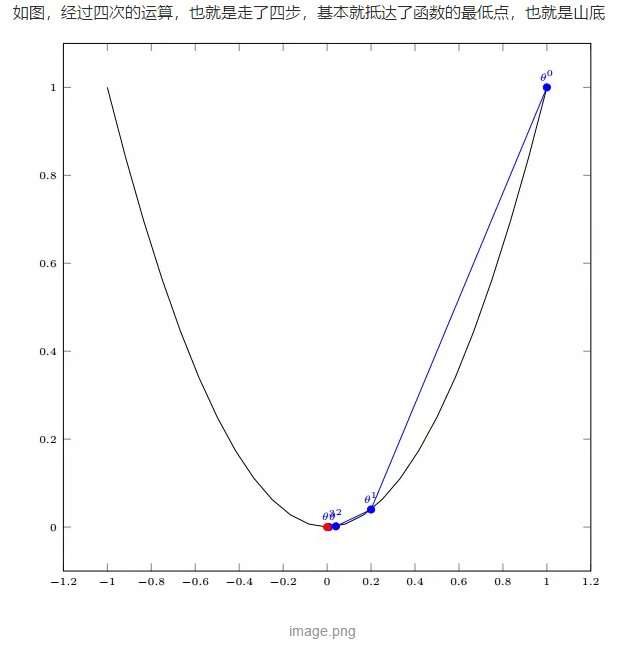


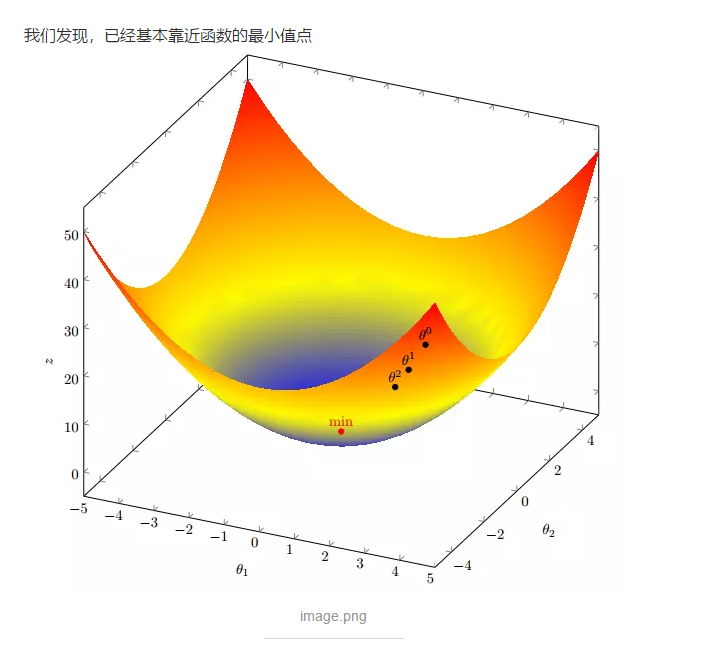
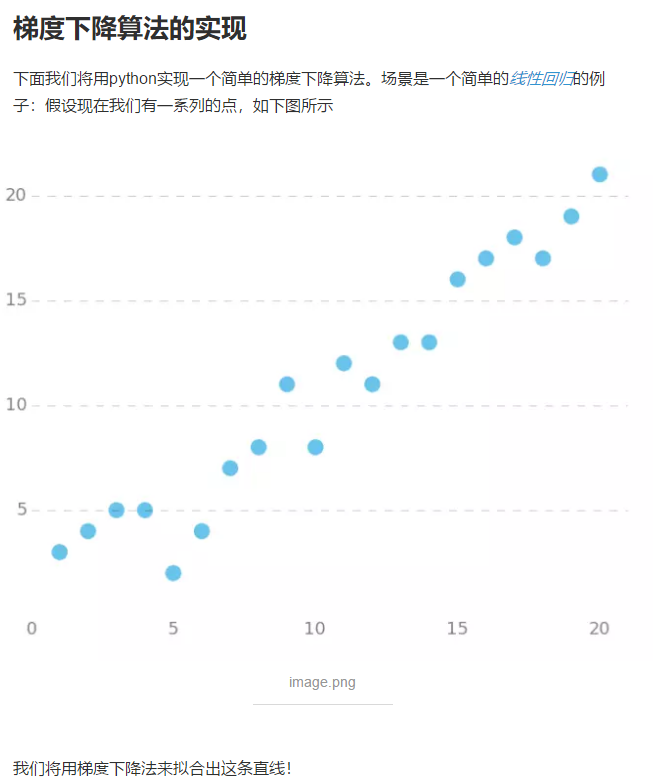




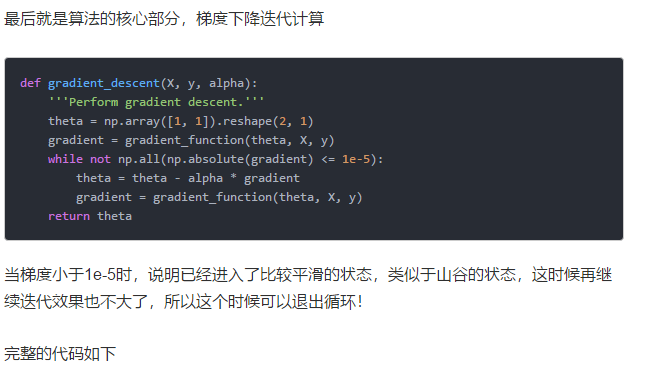
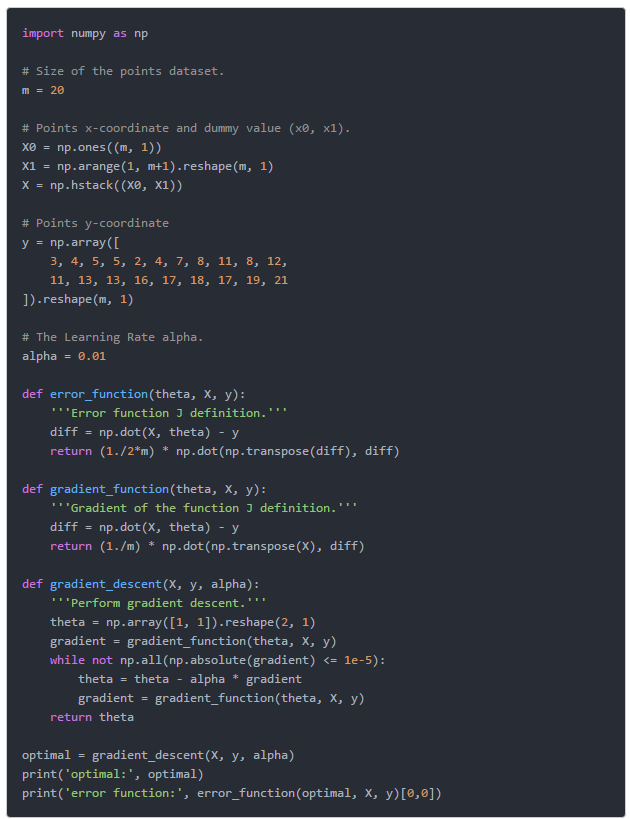

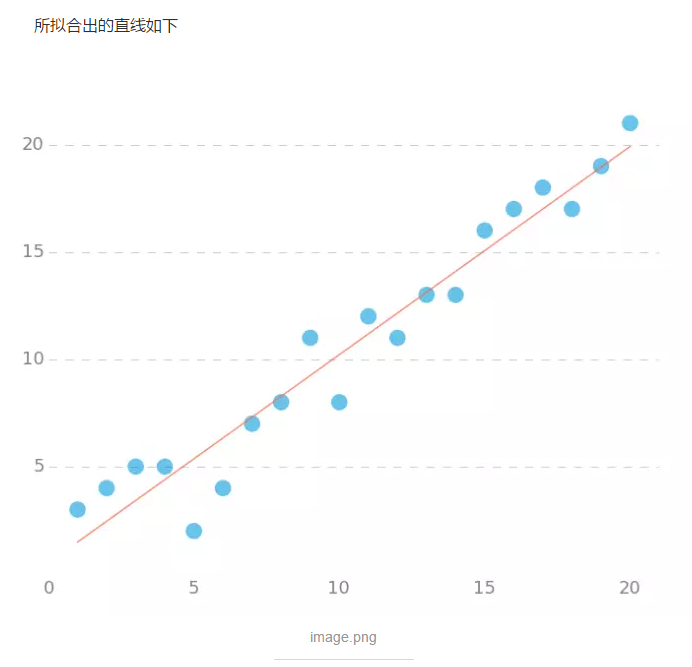

简单证明:

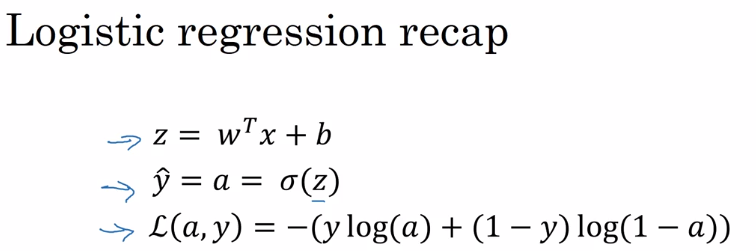

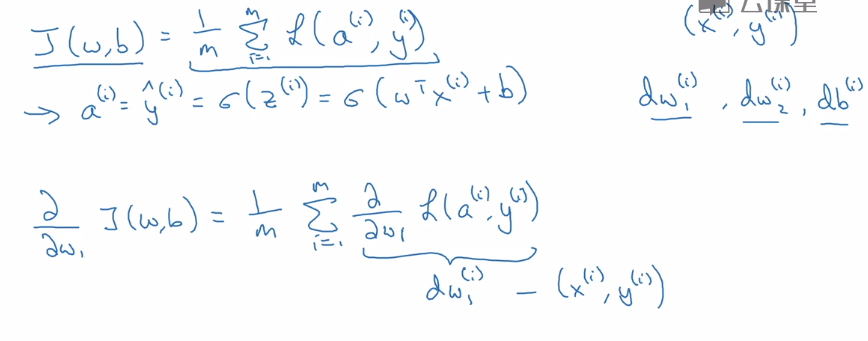




 浙公网安备 33010602011771号
浙公网安备 33010602011771号