后缀数组小结
后缀数组 (\(\rm Suffix Arrray\))小结
借用了一下别人的 \(\rm blog\)。
有关后缀数组 (\(\rm SA\))
介绍一下基本数组。
我们把原串 \(\rm A\) 的所有后缀按字典序从小到大排个序，
则排名为 \(\rm i\) 的字符串是以第 \(\rm sa_i\) 个字符为起点的，且以第 \(\rm i\) 个字符为起点的后缀的排名是 \(\rm rk_i\)。
所以有 \(\rm sa_{rk_i}=i\)。
得到 \(\rm sa,rk\) 的方法是基数排序 + 倍增。
基数排序的思想就是按从低位到高位将数排序，可以做到 \(\rm O(|A|)\)。
那么求出 \(\rm sa\) 的总时间复杂度是 \(\rm O(|A|\log |A|)\) 的。
解释一下代码：
假设原串是这样的：
m=122;
for(int i=1;i<=n;++i) ++cnt[x[i]=A[i]];
for(int i=2;i<=m;++i) cnt[i]+=cnt[i-1];
for(int i=n;i;--i) sa[cnt[x[i]]--]=i;
这里 \(\rm cnt\) 是一个桶，用来记录每个字符出现的次数，\(\rm m\) 表示桶中数最大值是多少 (因为只有大小写英文字母或数字所以只需要 \(\rm 122\))。
这个代码也很好理解，就是对单个字符 (第一关键字)的排序。
排完序后 \(\rm sa\) 数组长这样：
for(int k=1;k<=n;k*=2){
这表示倍增。
int t=0;
for(int i=n-k+1;i<=n;++i) y[++t]=i;
for(int i=1;i<=n;++i)
if(sa[i]>k) y[++t]=sa[i]-k;
这表示对第二关键字的排序。
for(int i=1;i<=m;++i) cnt[i]=0;
for(int i=1;i<=n;++i) ++cnt[x[i]];
for(int i=2;i<=m;++i) cnt[i]+=cnt[i-1];
for(int i=n;i;--i) sa[cnt[x[y[i]]]--]=y[i],y[i]=0;
这里就直接结合两关键字的排序搞出了一个总排序。
\(\rm x\) 里面存了上次关键字的排序，在本次排序中即是第一关键字的排序，\(\rm x\) 的值排序等于第一关键字排序，这里的计数排序做的是对的。那么第二关键字呢？
前面对第二关键字进行了排序，在这里 \(\rm x_{y_i}\) 就是根据第二关键字的顺序重新改变了第一关键字的顺序，也就是说在本次计数排序中，出现先后次序排序等于第二关键字大小排序。
换句话说，我们先单独对第二关键字排序，根据这个顺序改变第一关键字的顺序，由于在计数排序时首先按照第一关键字的值排序，而第一关键字的值没有改变所以首先还是根据第一关键字排序，改变的是第一关键字相同的时候，出现在前面的第二关键字排在前面。
然后 \(\rm sa\) 长这样：
swap(x,y);
x[sa[1]]=1,t=1;
for(int i=2;i<=n;++i)
x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?t:++t;
if(t==n) break;
m=t;
这里我们就重新搞好了数组，可以继续倍增搞。
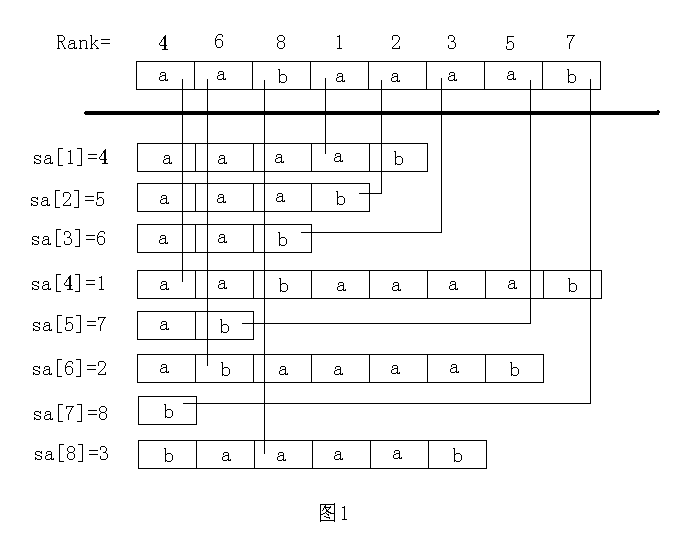
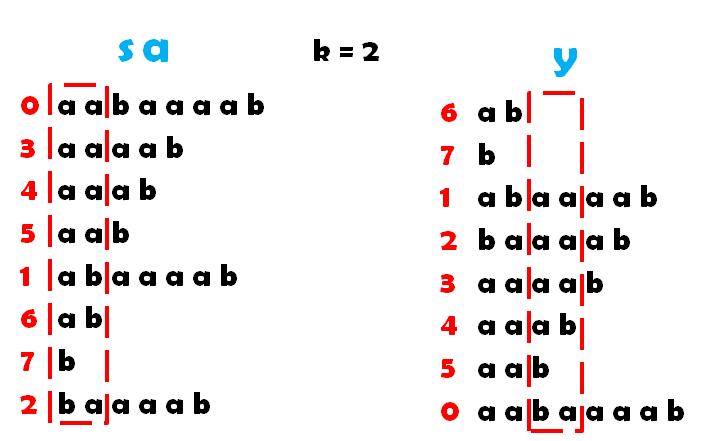
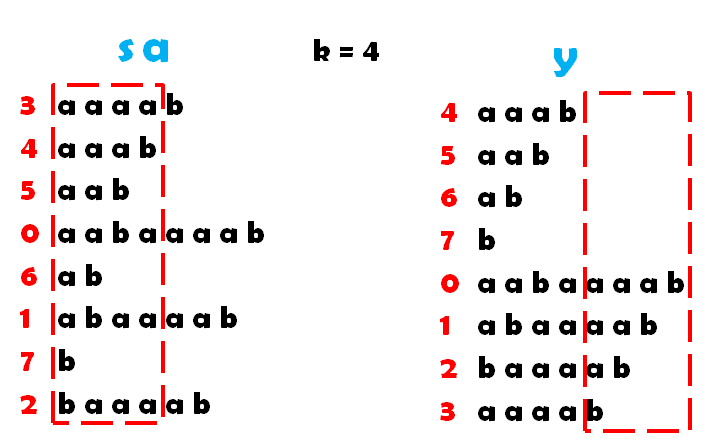
完整过程图片如下：
完整代码如下：
inline void get_sa(){
m=122;
for(int i=1;i<=n;++i) ++cnt[x[i]=A[i]];
for(int i=2;i<=m;++i) cnt[i]+=cnt[i-1];
for(int i=n;i;--i) sa[cnt[x[i]]--]=i;
for(int k=1;k<=n;k*=2){
int t=0;
for(int i=n-k+1;i<=n;++i) y[++t]=i;
for(int i=1;i<=n;++i)
if(sa[i]>k)
y[++t]=sa[i]-k;
for(int i=1;i<=m;++i) cnt[i]=0;
for(int i=1;i<=n;++i) ++cnt[x[i]];
for(int i=2;i<=m;++i) cnt[i]+=cnt[i-1];
for(int i=n;i;--i) sa[cnt[x[y[i]]]--]=y[i],y[i]=0;
swap(x,y);
x[sa[1]]=1,t=1;
for(int i=2;i<=n;++i)
x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?t:++t;
if(t==n) break;
m=t;
}
}
有关最长公共前缀 \(\rm LCP\)
\(\rm LCP(i,j)\) 表示后缀 \(\rm sa_i\) 与后缀 \(\rm sa_j\) 的最长公共前缀。
众所周知，后缀数组一点用都没有，用的都是后面有关 \(\rm LCP\) 的部分。
关于 \(\rm LCP\) 的性质，定理：
- \(\rm LCP(i,j)=LCP(j,i)\)
- \(\rm LCP(i,i)=|A|-sa_i+1\)
这两条性质可以把所有的 \(\rm LCP(i,j)\) 都转化为 \(i<j\) 的情况来求解。
- \(\rm \forall\ i\le j\le k,LCP(i,k)=\min(LCP(i,j),LCP(j,k))\)
- \(\rm LCP(i,k)=\min_{j=i+1}^k\{LCP(j,j-1)\}\)
定义 \(\rm height_i\) 表示 \(\rm LCP(i,i-1)\)，有 \(\rm height_1=0\)
那么由上述定理可得：
这样我们就可以用一个 \(\rm ST\) 表来 \(\rm O(|A|\log A)\) 预处理，\(\rm O(1)\) 求 \(\rm LCP\) 了
定义 \(\rm h_i=height_{rk_i}\)，同样的有 \(\rm h_{sa_i}=height_i\)。
那么还有一条定理：
- \(h_i\ge h_{i-1}-1\)，即 \(\rm height_{rk_i}\ge height_{rk_{i-1}}-1\)。
我们也就可以写出求 \(\rm height\) 的代码 (这里用 \(\rm ht\) 表示 \(\rm height\))：
inline void get_ht(){
int t=0;
ht[0]=0;
for(int i=1;i<=n;++i) rk[sa[i]]=i;
for(int i=1;i<=n;++i){
if(rk[i]==1)
continue;
if(t) --t;//h[i]>=h[i-1]-1
int j=sa[rk[i]-1];
while(j+t<=n&&i+t<=n&&A[i+t]==A[j+t])//上一次计算结果为t,那就从t开始检查有几个字符相同
++t;
ht[rk[i]]=t;
}
}
总代码：
int n,m;
int sa[N<<1],rk[N<<1],ht[N<<1];
char A[N];
struct SA{
int x[N<<1],y[N<<1],cnt[N<<1];
inline void get_sa(){//后缀数组
m=122;
for(int i=1;i<=n;++i) ++cnt[x[i]=A[i]];
for(int i=2;i<=m;++i) cnt[i]+=cnt[i-1];
for(int i=n;i;--i) sa[cnt[x[i]]--]=i;
for(int k=1;k<=n;k*=2){
int t=0;
for(int i=n-k+1;i<=n;++i) y[++t]=i;
for(int i=1;i<=n;++i)
if(sa[i]>k)
y[++t]=sa[i]-k;
for(int i=1;i<=m;++i) cnt[i]=0;
for(int i=1;i<=n;++i) ++cnt[x[i]];
for(int i=2;i<=m;++i) cnt[i]+=cnt[i-1];
for(int i=n;i;--i) sa[cnt[x[y[i]]]--]=y[i],y[i]=0;
swap(x,y);
x[sa[1]]=1,t=1;
for(int i=2;i<=n;++i)
x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?t:++t;
if(t==n) break;
m=t;
}
}
inline void get_ht(){//求 height 数组
int t=0;
for(int i=1;i<=n;++i) rk[sa[i]]=i;
for(int i=1;i<=n;++i){
if(rk[i]==1){
continue;
}
if(t) --t;
int j=sa[rk[i]-1];
while(j+t<=n&&i+t<=n&&A[i+t]==A[j+t])
++t;
ht[rk[i]]=t;
}
}
}t1;
\(\rm luoguP3809\)
板子题，甚至不需要求 \(\rm height\)
代码放过了
