关于多级放大电路截止频率的估算的修正系数

在《模拟电子技术基础》中，截止频率估算一节，关于多级放大电路的截止频率的修正系数，写的是1.1。

参考书是米尔曼的《微电子学：数字和模拟电路与系统》中册，111-112页。

 

 

于是我就查了这本书，并下载了对应的章节，第13章。但是这个系数的计算，指向了习题13-51。

于是，我就又买了习题册，查了一下，这个系数的来源很简单。

先计算二级放大，再计算三级放大，然后确认这个系数的误差很小，不超过10%。

另外，这个系数有个条件，就是各级的极点相差不是很远（或者很多考试题，都是多级极点相同）。

这里假设各级的极点相同。

 

在这个前提下，得到了一个1.1的系数：

 

 基于习题的13-51的推理，计算完二级再验证三级，太麻烦且没有说明系数的实际来源，只是表明是试验验证的结果。

我们不用那么麻烦，直接计算2^(1/n)的值，应该可以更快一些。

假设f(x)=2^x，计算泰勒级数：

f(x)=1 + ln(2) * x + [ln(2) * ln(2)]/2 * x^2 + Rn(x)。

忽略高次项x^2，那么f(1/n)=1+ln(2)/n

所以sqrt[2^(1/n)-1]=sqrt[ln(2)/n]=0.833/sqrt(n)，所以系数就是1/0.833=1.2。

接下来我们就用1.1和1.2的系数，分别计算2-10级的放大电路的高频截止系数，来对比一下计算结果：

 

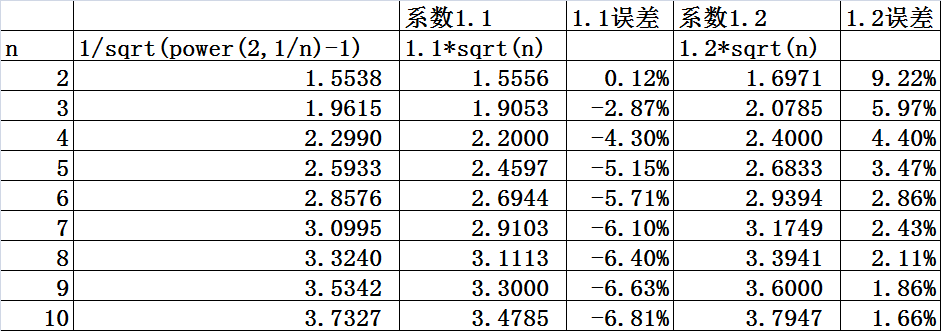
  从表格对比来看，如果每级的极点相同时，以4级放大为分界，4级以下，采用1.1的系数比较准，而4级以上，采用1.2的系数比较准。

这是因为4级以下，靠试验数据修正得来的系数；

而4级以上，泰勒公式估算比较准确。因为忽略的是2次方项，所以n越大，1/n越接近零，估算越准确，所以最大误差发生在n=2时，并且误差随着n的增大不断减小。

同样，因为1.1和1.2的误差也没有超过10%，所以，n大于4时，估算时使用1.1也可以得到正确的结果。

这里进行推理计算一下，可以对多级放大电路的截止频率估算有个更清晰的认识。