零点、极点以及用零点抵消极点的实例

传递函数是复频域内，输出响应的拉普拉斯变换与输入激励的拉普拉斯变换的比值。在求传递函数时，有一个条件限制，就是初始条件为零。很多人并不会重视这个条件，但是想要使用叠加定理，初始条件为零，是必须满足的。

零点，是传递函数的分子为零的点，从数学上来说，传递函数分子为零，那么分数就为零，而Vout(s)=H(s)*Vin(s)，那么输出也为零，但是伯德图上却不是零。注意，拉普拉斯变换的s是复数，s=σ+jω，但是当绘制伯德图时，是令s=jω,然后绘制的传递函数的幅频曲线和相频曲线，也即是说只考虑了虚部，并没有考虑实部。

那为什么可以在绘制增益曲线的时候使用s= jω呢？ s=σ+j0=σ时，exp(s)是指数函数；而在s=0+jω=jω时，exp(s)是正弦函数。而伯德图是假设输入为正弦信号，当频率变化时，幅值和相位的变化，所以是使用s= jω。综合起来，零点的时候，输出不为零。

来看一个单零点的实例。近似的描述，在零点处fz，幅度增益增加3dB，相位超前45度，在零点之后，幅度增益的增长斜率为20dB/10倍频程，或者说6dB/倍频程。增益增加是从fz/10频率点开始，此时相位开始超前；到fz频率点时，增益增加3dB，相位超前45度，增益到10*fz时，相位超前90度。此后，增益继续增加，而相位近似不再变化。

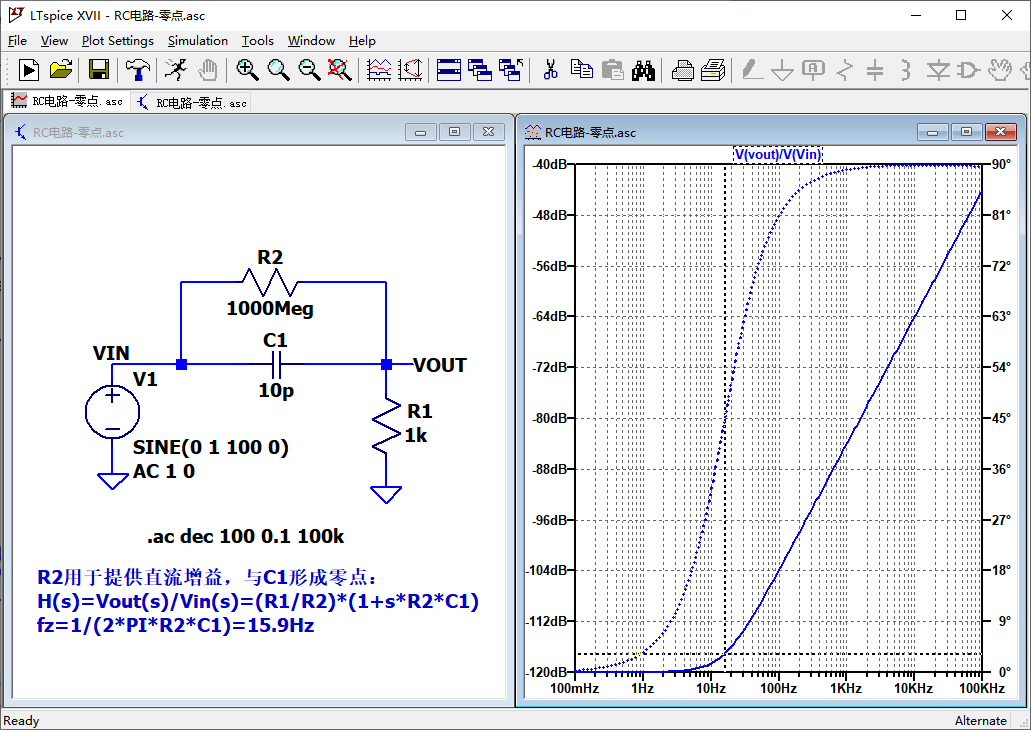
再看一个单极点的实例。近似的描述，在极点fp处，幅度增益减少3dB，相位滞后45度。相位从fp/10的频率点处开始滞后，在fp频率点处滞后45度，在10*fp频率点处，相位滞后90度，之后近似不再变化。

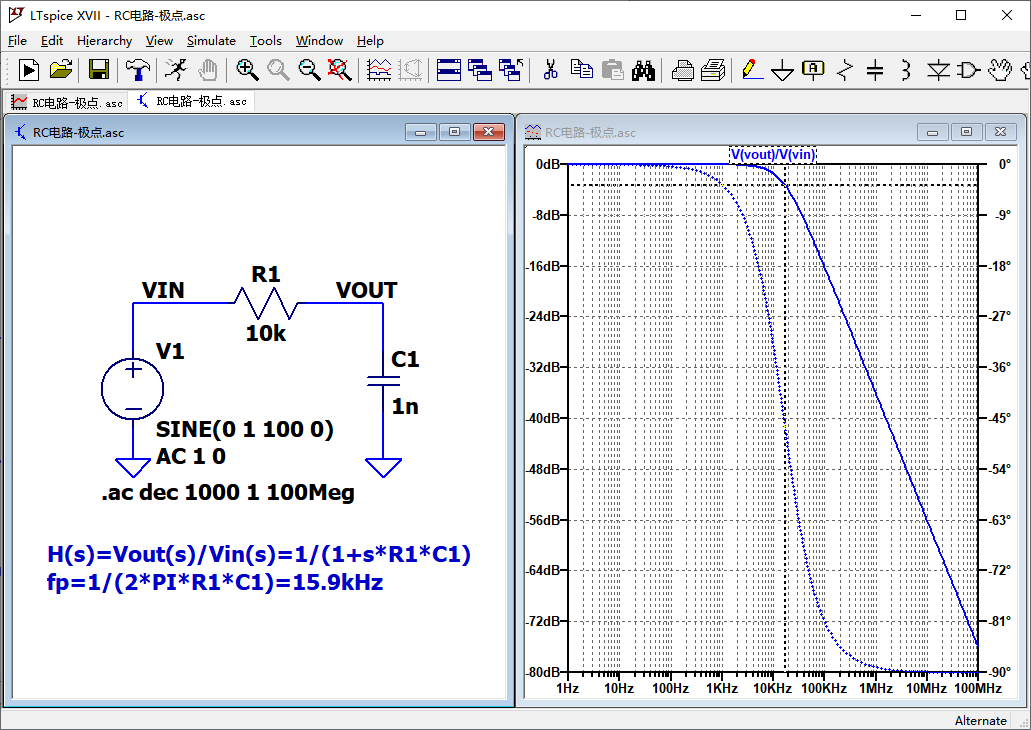
以上这些是零点和极点的一些基础知识。对于n阶极点和零点，就继续叠加即可。

接下来看一个简单实用的零点补偿极点的例子。在I-V转换电路中，通常需要在反馈电阻RF上并联一个小电容CF，防止输出端连接容性负载时发生振荡。如下图所示，CL和RL用来模拟连接负载。增加电容后，传递函数为H(s)=-RF/(1+s*RF*CF)，直流增益是160dB，即20*log(100Meg)。当频率逐步增大时，增益开始衰减，并且相位开始滞后。

这样，这个I-V转换电路用于直流测量是没有问题，但是用于交流测量，频率增大时，就会产生误差。当电阻很大时，CF可能是电阻两端的等效电容(这里为了方便演示，CF取值比较大)。

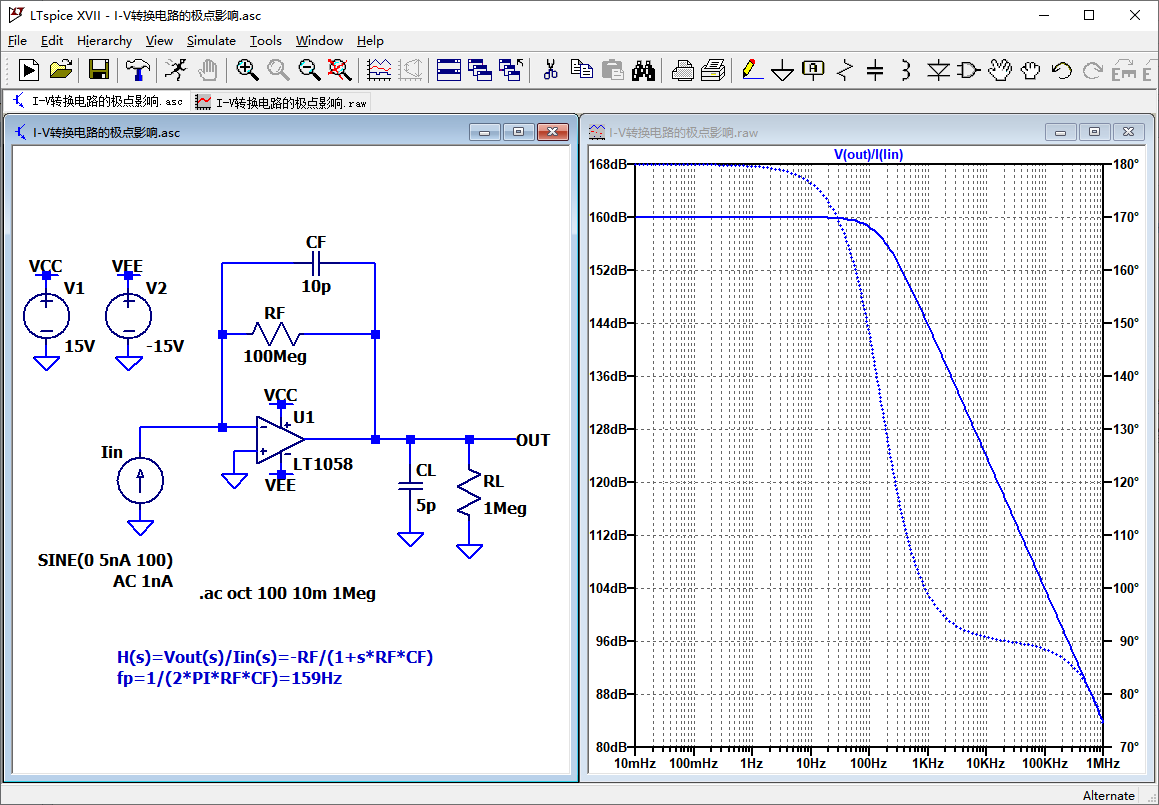
这时，就需要抵消掉这个极点。如下图所示：

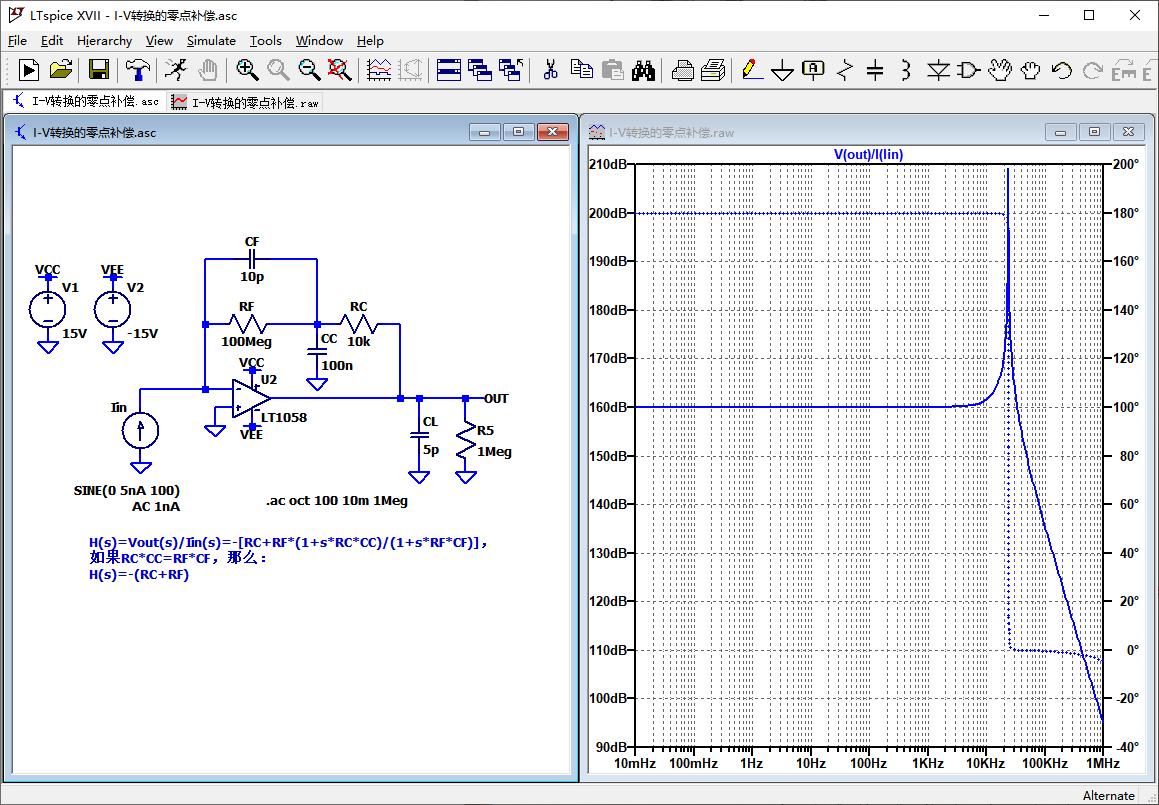
由CC和RC构成一个零点，用于补偿这个极点。可以看到，补偿后，交流频率一直到1kHz时，增益都没有发生变化。但是增益曲线大约在10kHz之后，出现谐振峰值，也就是说，时域会出现振铃或者小幅的高频振荡。在时域仿真一下有补偿和无补偿的对比波形如下。

 

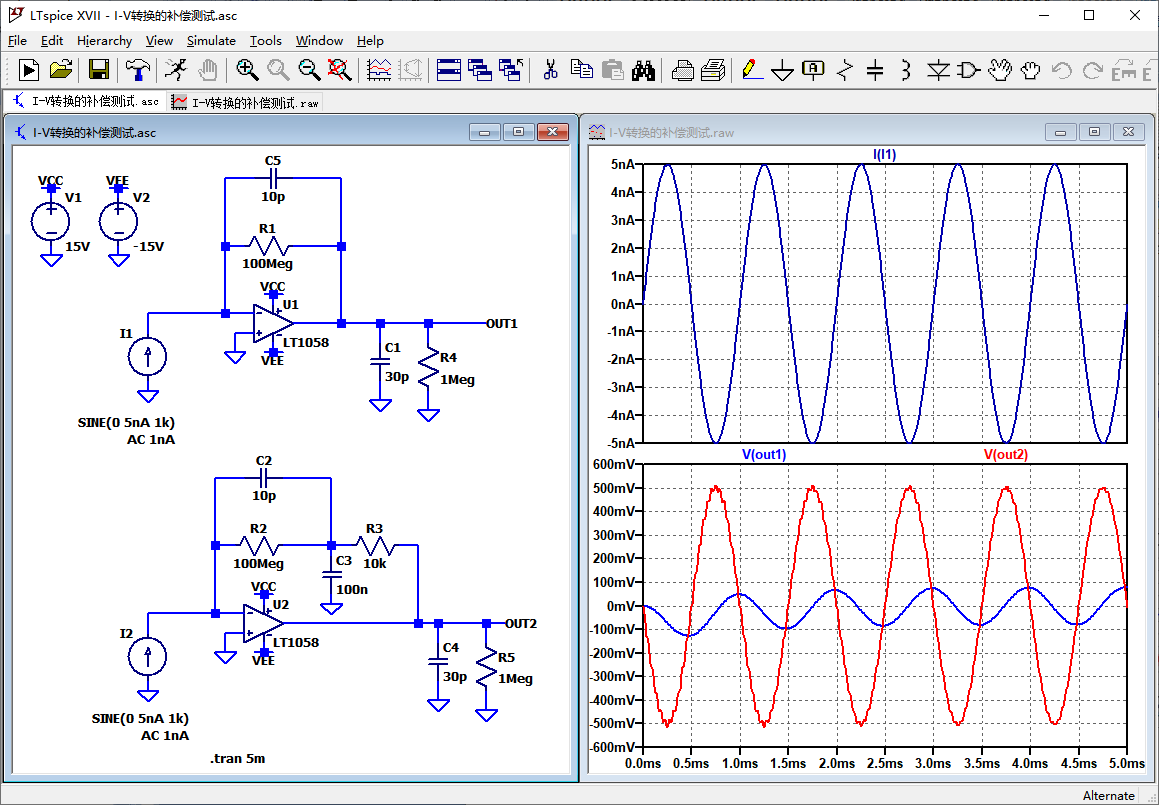
可以看到，使用零点补偿掉极点之后，在1kHz的输入电流时，输出幅值正常，输出相位也没有发生变化，只是在开始的几个周期，幅值上叠加有小幅的振铃。

而没有补偿掉极点的输出，衰减严重，且发生了相移。这与频域的仿真结果是对应的。在这个电路中，零点补偿抵消极点，就提高了输入信号的频率，但是输出的振铃就无法消除，所以后级电路必要时就需要增加滤波电路，截止频率低于I-V转换的幅频特性的谐振峰值频率，来衰减掉放大信号中叠加的振铃或者小幅振荡。这也是一些使用精密I-V转换电路的仪器的常用手段。

理想的元器件是不存在任何寄生参数的，但是现实毕竟是现实，每一种元件都有它的寄生参数，是无法消除的。这时候，就需要用各种方法，抵消掉这些寄生参数的影响。

这里留一个疑问，为什么理论分析的传递函数，H(s)=-[RC+RF*(1+s*RC*CC)/(1+s*RF*CF)]，在RC*CC=RF*CF时，H(s)=-(RC+RF)，是完美的不受频率的影响，但是仿真在高频段还是会受到频率的影响，而且幅频特性曲线上还出现了谐振峰，为什么？