浅谈Tarjan算法
- 本文略带简单证明,如有遗漏错误之处,还请不吝指出
有向图tarjan
强连通分量(简单来说)->一个极大子图,其中的点可以互相到达
我们设dfn为时间戳,low为最早能到达的点
当遇到新点时low和dfn初始化为++cnt
先介绍下搜索树中的4种边(实际上重要的只有3种边):
- 1.后向边->指向未搜索到的点的边
- 2.前向边->指向当前搜索栈中的边(能从指向节点搜到当前节点)
- 3.横插边->指向搜索过的点的边(所指向点不在搜索栈中,区别于2)
(这3种边包含了所有种情况,剩余的边意义不大,本文不做讨论) - 4.树枝边->搜索树中的边
我们先考虑边1,”边1指向的点“ 能到的点,当前点一定能到,所以(当前点为u,指向点为v)low[u]=min{low[v]}
我们再考虑边2,当前点(u)是从搜索栈中搜索过来的,所以边2指向点(v)一定能走到u,u又能再次走到v,于是u,v和他们之间的点构成强联通分量。
接下来考虑边3,边3指向点(v)已经被搜过,且当前点(u)又是新搜到的点,这就说明 点v后向边(1)所连接的所有节点都无法到达u,而点v前向边(2)所指向的节点如果能到u,则v一定还在搜索栈中(一个点如果所有边都遍历过了,且dfn=low才会和它的强联通分量一起出栈)
最后如果一个点(u)的dfn==low就把它和栈中所有在它后面的点出栈,标记为一个强联通分量
所有栈中的点如果没有出栈,一定是dfn!=low也就是能到达栈中其它点,而 ”u后面的点“ 都是可以从u遍历到的,u后面的点 能到达的点,u也能到,所以u就是u后面所有点能到的最早节点。
放张图画得太丑见谅
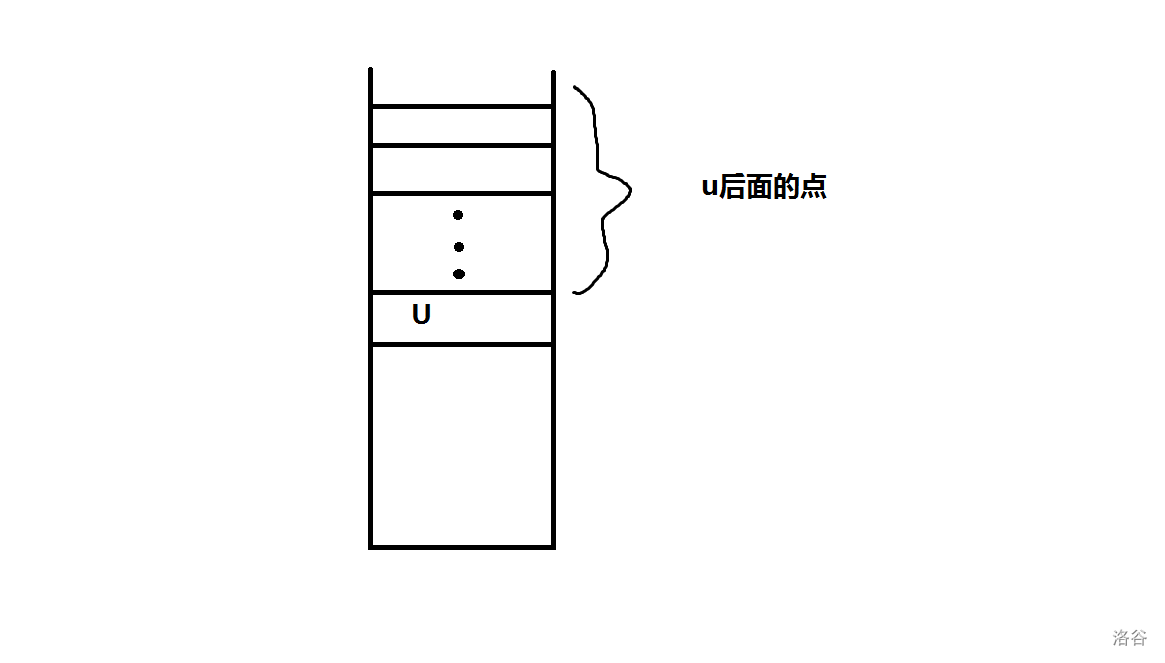
这里给出模板
void tarjan(int x){
s[stop++]=x;
dfn[x]=low[x]=++cnt;
for(int y,i=head[x];i;i=nxt[i]){
y=ver[i];
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x],low[y]);
}else if(!sccnum[y]) low[x]=min(low[x],dfn[y]);//在栈中
//注意这里无论是写dfn[y]还是low[y]都是对的,实际上无论对
//谁取min都不能准确的求出点x最早能到的节点,但可以标记
//点x属于一个强连通分量,这里写成dfn是为了和求割点统一
}
if(dfn[x]==low[x]){
++scccnt;//连通分量个数
do{
sccnum[s[--stop]]=scccnt;
}while(s[stop]!=x);
}
}
无向图tarjan
同样dfn=时间戳,low为最早能到达的点
因为无向图的点互相联通,无向图上tarjan主要是求割点和割边
这里引入两个概念
- 点双连通分量(简单来说)->一个极大子图,割掉其中任何一个点剩余点依然可以相互到达
- 边双连通分量(简单来说)->一个极大子图,割掉其中任何一条边,剩余点依然可以相互到达
求割点(割掉后图不再联通)
分两种情况
- 1.当前点是根节点
- 2.当前点不是根节点
首先考虑2,当前点如果不是根节点,只需要判断(x为当前点,y为边指向点) low[y]>=dfn[x]即可,因为如果x的儿子到不了x的前面(如果无法到达,y整个连通块编号都大于x),那割掉x后图中至少会有两部分不联通(x前面,和y所在连通块)
接着考虑1,如果根节点有两个不相连的儿子,那根节点就是割点
看一下具体代码
void tarjan(int x){
dfn[x]=low[x]=++cnt;
int sz=0;
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x],low[y]);
++sz;
if(dfn[x]<=low[y]&&x!=start) vis[x]=1;
//如果点y没有通过当前边就能到达 “能到达x点”的点,说明
//即使割掉点x,y依然和到点x前面(在栈中)的点连通,
//对于y来说x就不是割点,否则一定是割点。
}
low[x]=min(low[x],dfn[y]);//使用dfn[y]防止走当前边
//因为是无向图,所以不要求在栈中
}
if(x==start&&sz>=2) vis[x]=1;
if(vis[x])++sum;
}
再放张图,紫色为搜索顺序
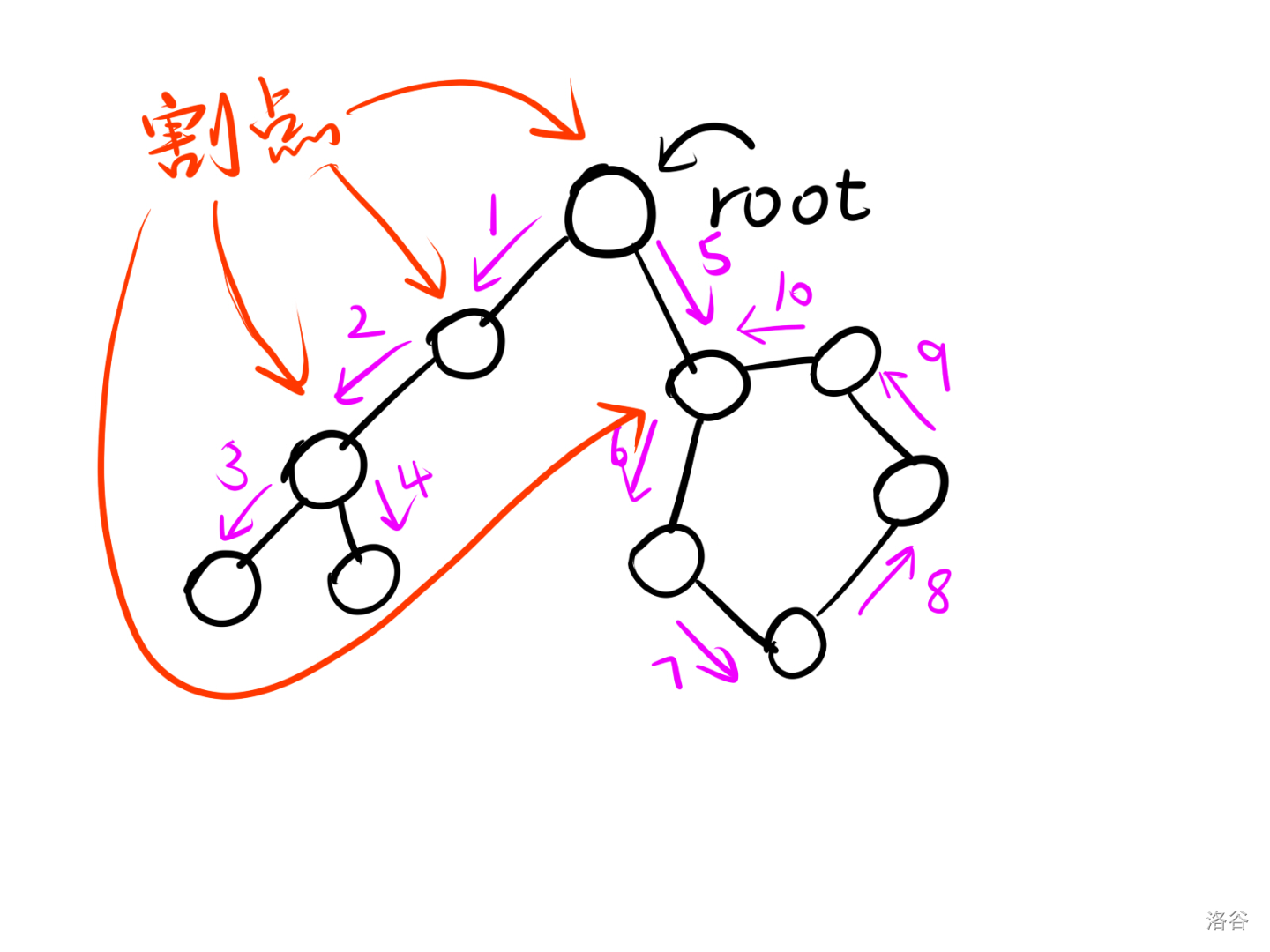
小技巧
点双连通分量中任意两点都至少有两条不经过重复点的路径
证明 :假设只有一条路径,则割掉路径上的一个点,子图就会分裂成两个,不满足点双连通分量定义
求完割点后只需要把割点打上标记,不去遍历,就可以把割点分开的部分缩点。
求割边(割掉后图不再联通)
dfn=时间戳,low=能到达的最早点
有两种求法
1:
考虑当前边连接u,v,当前节点为u,如果点v不走当前边无法到达u前面的点,说明当前边是割边。
代码
void tarjan(int x,int ff){
dfn[x]=low[x]=++cnt;
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(i==ff) continue;
if(!dfn[y]){
tarjan(y,i^1);
//存双向边的时候初始化tot=1,这样编号^1就是反边
low[x]=min(low[x],low[y]);
if(dfn[x]<low[y]) cut[i]=cut[i^1]=true;
//只有在连接一个没有遍历过的点的时候,i才可能是割边
//一个小小的卡常
}else low[x]=min(low[x],dfn[y]);//同理
}
}
2:
考虑当前点(u)和来边 from
如果点u的dfn==low那点u及在点u后面的所有有点都到不了u的前面,此时from就是割边
代码
void tarjan(int x){
dfn[x]=low[x]=++cnt;
s[stop++]=x;
for(int y,i=head[x];i;i=nxt[i]){
if(i==from[x]^1) continue;//存边方法和原来一样 初始化tot=1,2和3为一对边
if(!dfn[y=ver[i]]){
from[y]=i;
tarjan(y);
low[x]=min(low[x],low[y]);
}else low[x]=min(low[x],dfn[y]);//还是无所谓dfn还是low,因为来的边已经continue掉了
}
if(dfn[x]==low[x]){
++scccnt;
cut[from[x]]=cut[from[x]^1]=true;
do{
sccnum[s[--stop]]=scccnt;
//边双连通分量也能求出
}while(s[stop]!=x);
}
}
两者时间复杂都是O(n)
1求连通分量是O(m),因为并查集每个节点都询问一次总体复杂度是O(m)的(看下文)
再来个图,紫色为遍历顺序
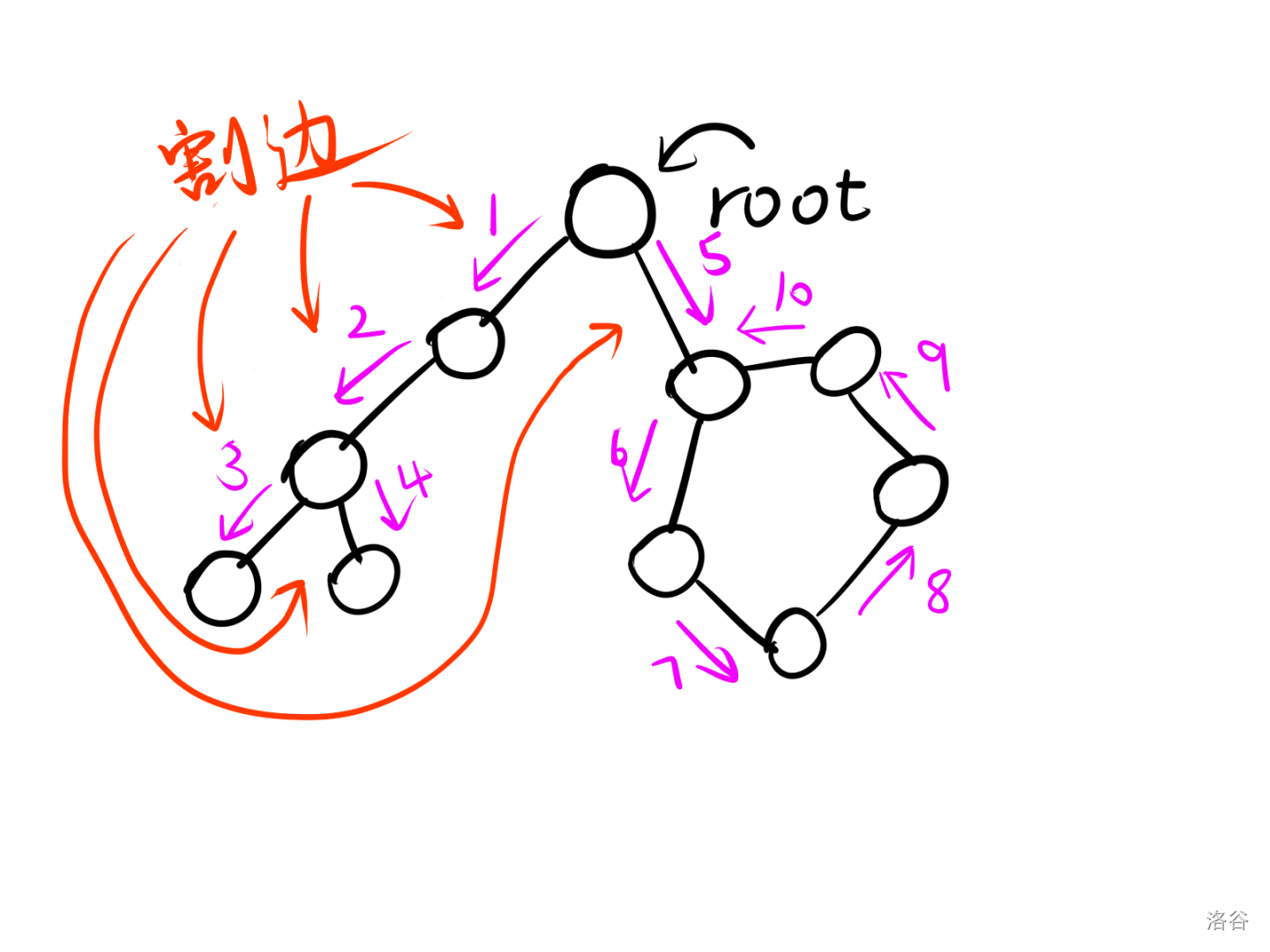
小技巧
边双连通分量中任意两点都至少两条有不经过重复边的路径
证明 :同上
用1求完割边后我们怎么缩点?
使用并查集维护!
考虑所有非割边,它所连接的两个点一定在同一个边双联通分量。
例题
推荐题目: luogu试炼场 强连通分量。。。
加餐
一本通1729
问题简化:如何确定无向图上从s到t有一条(经过“满足XXX条件的边”的“不经过重复边”)路径?
从s向t连一条不满足XXX条件的边,这样如果s有到t的路径则一定在s和t的边双联通分量里,枚举边检查即可。
一本通 1730:二分图
首先跑二分图匹配(匈牙利or网络流),对于每条匹配边,从左边节点向右边节点连一条有向边,对于每条非匹配边,从右往左连一条有向边,如图,红色是匹配边,黑色是非匹配边
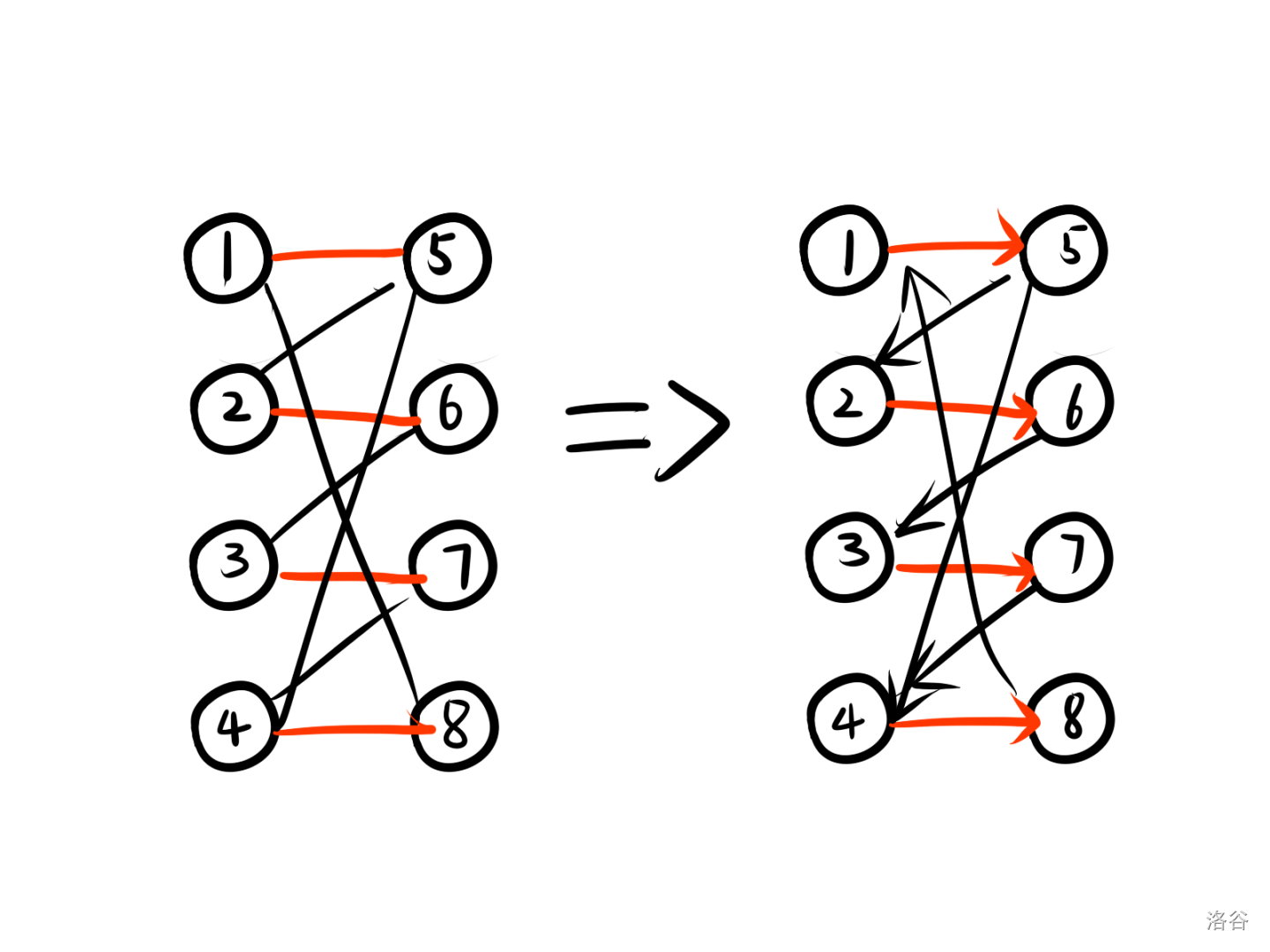
如果匹配数小于n,说明没有一条边符合要求
如果当前边是匹配边,这条边符合要求
考虑n=m
如果一条非匹配边所连接的两个点在同一强连通分量里,则这条边符合要求,因为如果从右侧的点一条非匹配边、一条匹配边的走,如果可以走回来,那这两个点就在同一个强连通分量里,这时我们让非匹配边变成匹配边,匹配便变成非匹配边,则当前非匹配边符合要求
考虑n!=m
就会出现下面红黑线连的情况
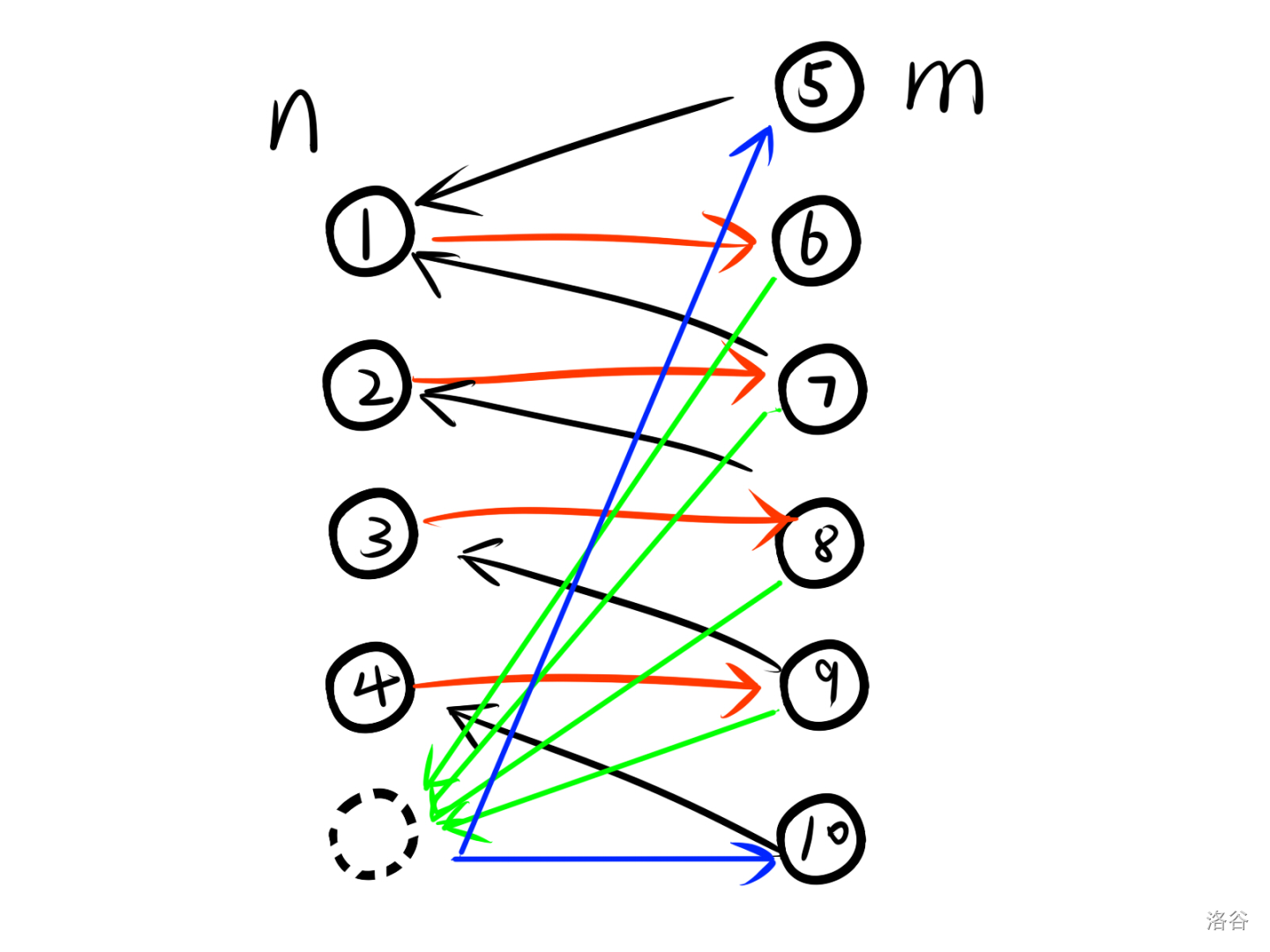
这时我们只需要新建一个节点,让所有匹配边右面的点连向新点,新点连向所有非匹配边右边的点
这时如果一个边满足要求,它要么是第一种情况,要么,可以走到一个非匹配边右面点再走回来,这时对路径上的边取反,则当前边符合要求
-
code
卡了下常,所以码的十分毒瘤。。。
一本通 1731:最大流
这些都是书:信息学奥赛一本通-高手训练上的题,感觉比较有价值,就放上来,由于书上这道题的题解写的很好,我就荡过来了老实交代,一本通给了你多少钱。。。
注意到题目中点的度不超过3,则两点间的最大流也不超过三,由于最大流又等于最小割,可以从最小割入手考虑两个点(i,j)之间的最大流情况:
1.最小割为0:则点i,j不连通,可以用并查集维护判断。
2.最小割为1:则点i,j联通,但属于不同的边双联通分量,直接用tarjan求解判断;
3.最小割为2 :则存在一条边被删除后i,j联通,但属于不同的边双连通分量,此时可以枚举每条边,将其删除后再tarjan,记录下每个点在每条边被删除后所属的双连通分量编号。显然每个点都有m个编号,那么对于i,j,只要这m个编号一一对应,就说明会出现情况3。考虑到之需要判断m个编号是否完全一致,可使用hash进行维护,可以使用自然溢出。
4.如果不属于以上3种情况,则最小割为3。
时间复杂度O(M×(N+M))
一开始我竟然想最小割树+HLPP卡常过这题,怕不是高级算法学傻了。。
P4747 [CERC2017]Intrinsic Interval
设原数列为a[i]
对于询问(l,r),如果l==r显然答案就是(l,r)
考虑r-l>=1的情况,我们设点i代表选点i和点i+1,p[i]代表权值为i的数的位置,对于点i(选i和i+1),我们设l=min(a[i],a[i+1]),r=max(a[i],a[i+1]),那选择点i就要选择min(p[lr])到max(p[lr])-1位置的所有点,这样将问题转换为连通性问题,把点i和min(p[lr])到max(p[lr])-1的所有点连边,显然对于一个强连通分量可以看成一个点,这样图变成一个dag,用拓扑排序求出每个(点所属的强联通分量)能到达的 最左最右区间即可。
考虑到要建的边很多,而所需连边的点又是一段区间我们可以线段树优化建图。
区间最大~最小值可以线段树orST表or平衡树解决
这里简单提一下线段树优化建图,已知线段树上每个节点代表一个区间,首先每个节点要向自己儿子连边,这样每次一个新点向一段区间连边就只需要连log条


 浙公网安备 33010602011771号
浙公网安备 33010602011771号