part0 什么是多项式？
\[f(x) = \sum\limits_{i = 0}^{n - 1} a_i * x^i
\]
点值表示
\((x_0,f(x_0)),(x_1,f(x_1))...(x_{n-1}, f(x_{n-1}))\)
part1 离散傅里叶变换
复数
首先我们要了解复数 即 $i = \sqrt {-1} $
一个数有实部和虚部 即 \(a = x + y * i ~~ (x, y)\)
原来的实数运算相当于在一个一维数轴上进行移动，复数则是在二维平面上运动
复数运算
一句话来说就是 摸长相乘，幅角相加
c++中提供了复数模板
#include <complex>
complex <double> a;
可以像正常数一样加减乘除
单位根
下面默认 \(n\) 是２的整数次幂, 不够在末尾补０
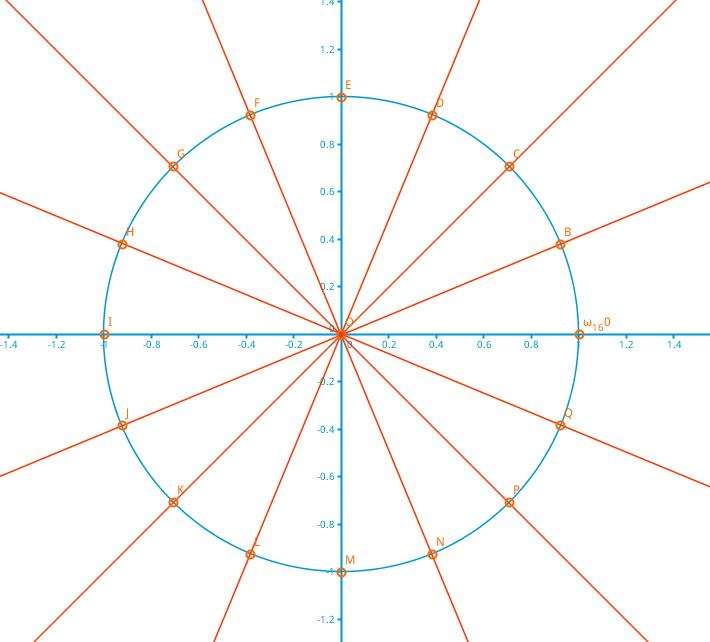
对于一个 \(n\) 次多项式我们把一个单位圆分成 \(n\) 份
\[\omega_n^0, \omega_n^1, \omega_n^2,...,\omega_n^{n - 1}
\]
\[\omega_n^k = (cos(\frac k n * 2 * \pi), sin(\frac k n * 2 * \pi))
\]
\(\omega_n^k\) 叫做单位根 , \(\omega_n^1\) 就叫做 \(n\) 次单位根 , 根据复数运算 \(\omega_n^k = (\omega_n^1)^k\)
单位根性质
\[\begin{cases} \omega_{2n}^{2k} = \omega_n^k \\\omega_n^{k + \frac 2 n} = - \omega_n ^ k \end{cases}
\]
都比较显然把。。。
把 \(\omega_0, \omega_1, \omega_2,...,\omega_{n - 1}\) 带入多项式,得到 \(f(\omega_0), f(\omega_1), f(\omega_2),...,f(\omega_{n - 1})\)，\(\{(\omega_i, f(\omega_i))\}\) 这种点值表示就是离散傅里叶变换
离散傅里叶变换的逆变换
设 \(y_0, y_1, ... , y_{n -1} = f(\omega_n^0), f(\omega_n^1), ... , f(\omega_n^{n - 1})\)
设函数
\[F(x) = \sum\limits_{i = n}^{n - 1} y_i * x^i
\]
将单位根的倒数 \(\omega_n^{-0}, \omega_n^{-1},...\omega_n^{-(n - 1)}\) 带入 \(F(x)\)
得到
\[z_k= F(\omega_n^{-k})= \sum_{i = 0} ^ {n - 1} y_i * \omega_n^{-k}
\]
\[= \sum_{i = 0} ^ {n - 1} \sum_{j = 0} ^ {n - 1} a^j * (\omega_n^i) ^ j * (\omega_n^{-k}) ^ i
\]
\[=\sum_{j = 0} ^ {n - 1} a^j \sum_{i = 0} ^ {n - 1} (\omega_n^j) ^ i * (\omega_n^{-k})^i
\]
\[=\sum_{j = 0} ^ {n - 1} a^j \sum_{i = 0} ^ {n - 1} (\omega_n^{j - k})^i
\]
根据等比数列求和公式
\[z_k = a_k * n
\]
\[a_k = \frac {z_k} n
\]
这样，我们用点值表示推出了系数
快速傅里叶变换
已知
\[f(x) = \sum a_i * x^i
\]
把 \(f(x)\) 分成奇偶两部分
\[f(x) = (a_0x^0 + a_2x^2 + a_4x ^ 4 + ...) + (a_1 x ^ 1 + a_3 x ^3 + a_5 x ^ 5 + ...)
\]
设
\[\begin{cases} A(x) = a_0x^0 + a_2 x ^ 1 + a_4 x ^2... \\ B(x) = a_1 x ^ 0 + a_3x^1 + a_5x^2...\end{cases}
\]
\[f(x) = A(x^2) + x * B(x ^ 2)
\]
把 \(\omega_n^k (k < \frac n 2)\) 带入
\[f(\omega_n^k) = A(\omega_n^{2k}) + \omega_n^k B(\omega_n^{2k})
\]
\[= A(\omega_{\frac n 2}^k) + \omega_n^k B(\omega_{\frac n 2} ^ k)
\]
把 \(\omega_n^{k + \frac n 2} ( k < \frac n 2)\) 带入
\[f(\omega_n^{k + \frac n 2}) = A(\omega_n^{2k} * \omega_n^n) -\omega_n^k B(\omega_n^{2k} * \omega_n^n)
\]
\[= A(\omega_{\frac n 2}^{k}) - \omega_n^k B (w_{\frac n 2}^k)
\]
n = 1时直接返回就行了
