P3756 [CQOI2017] 老C的方块

原题链接

感觉挺有意思的。

先简化一下不合法的状况，实际上是如果特殊边两侧都有点，且那两个点的另外三个联通方向上也有至少一个点，就是坏的。相当于是四个限制只要有一个不满足就可以了。于是就可以转化成最小割。

按四种限制将点分成四类。特殊边两侧分别是 \(1\) 类点和 \(2\) 类点，\(1\) 类点四联通的非 \(2\) 类点是 \(3\) 类点，\(2\) 类点四联通的非 \(1\) 类点是 \(4\) 类点。如下图所示。

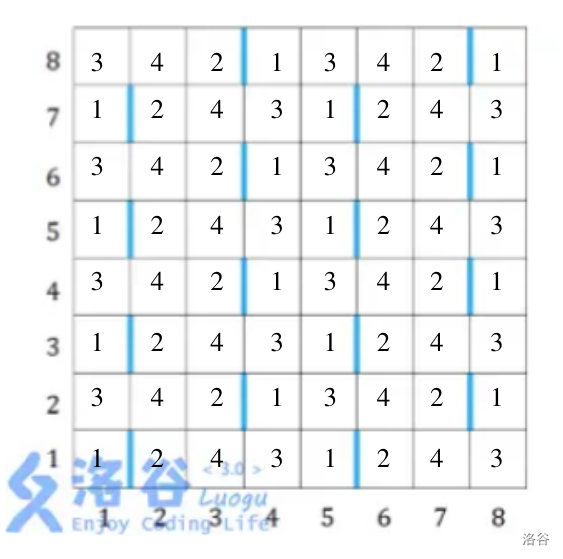
这样标号以后，我们就可以通过在不同编号的点中连边来做到从源点分别经过四条限制到达汇点。一个周期中的点就长这样：

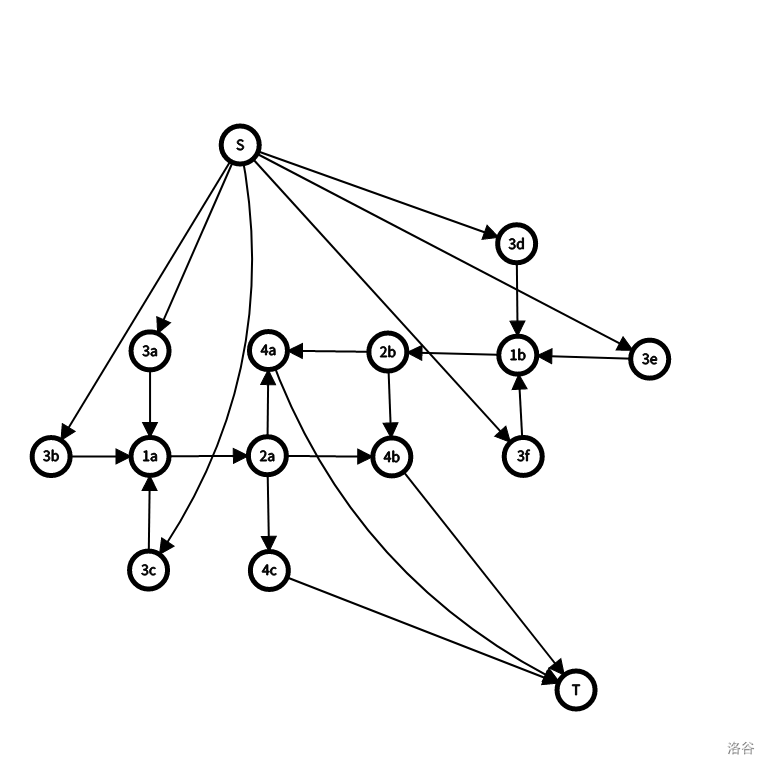
至于删掉每个格子的代价，\(3\) 类点可以在源点到它的边上将容量设为其权值，表示删掉 \(3\) 类点，\(3\) 类点到 \(1\) 类点的边上设为 INF 表示不能删。\(4\) 类点同理。

当然我们是可以删掉 \(1\) 类点和 \(2\) 类点的，只需要在 \(1\) 类点到 \(2\) 类点的边上将权值设为它俩权值中较小值即可。

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
#include<queue>
using namespace std;
using namespace __gnu_pbds;
const int MAXN=1e5+10,MAXM=4e5+10,INF=1e9+7;
int C,R,n,s,t,x[MAXN],y[MAXN],w[MAXN],dep[MAXN],ans;
int to[MAXM],nxt[MAXM],head[MAXN],cur[MAXN],val[MAXM],cnt=1;
gp_hash_table <int,int> p[MAXN];
inline void add(int x,int y,int v)
{
    to[++cnt]=y,nxt[cnt]=head[x];
    head[x]=cnt,val[cnt]=v;return ;
}
inline void edd(int x,int y,int v){add(x,y,v),add(y,x,0);}
inline bool bfs()
{
    for(int i=s;i<=t;++i) dep[i]=-1,cur[i]=head[i];
    dep[s]=0;queue <int> q;q.push(s);
    while(!q.empty())
    {
        int x=q.front();q.pop();
        for(int i=head[x];i;i=nxt[i])
        {
            int y=to[i];
            if(val[i]&&dep[y]==-1)  
                dep[y]=dep[x]+1,q.push(y);
        }
    }
    return dep[t]!=-1;
}
int dfs(int x,int flow)
{
    if(x==t) return flow;int rmn=flow;
    for(int i=cur[x];i&&rmn;i=nxt[i])
    {
        cur[x]=i;int y=to[i];
        if(!val[i]||dep[y]!=dep[x]+1) continue;
        int f=dfs(y,min(rmn,val[i]));
        rmn-=f,val[i]-=f,val[i^1]+=f;
    }
    return flow-rmn;
}
int main()
{
#ifdef ONLINE_JUDGE
    cin.tie(0),cout.tie(0);
    ios::sync_with_stdio(0);
#else
    freopen("in.in","r",stdin);
    freopen("out.out","w",stdout);
#endif
    cin>>C>>R>>n;s=0,t=n+1;
    for(int i=1;i<=n;++i)
    {
        cin>>x[i]>>y[i]>>w[i];
        p[x[i]][y[i]]=i;
    }
    for(int i=1;i<=n;++i)
    {
        int k=(x[i]&3)^(y[i]&1),j;//这里是用位运算确定是哪一类点。
        if(!k)
        {
            if((y[i]&1)&&(j=p[x[i]+1][y[i]])) edd(i,j,min(w[i],w[j]));
            if(!(y[i]&1)&&(j=p[x[i]-1][y[i]])) edd(i,j,min(w[i],w[j]));
        }
        if(k==3)
        {
            if((y[i]&1)&&(j=p[x[i]+1][y[i]])) edd(i,j,INF);
            if(!(y[i]&1)&&(j=p[x[i]-1][y[i]])) edd(i,j,INF);
            if(j=p[x[i]][y[i]+1]) edd(i,j,INF);
            if(j=p[x[i]][y[i]-1]) edd(i,j,INF);
        }
        if(k==1)
        {
            edd(s,i,w[i]);
            if((y[i]&1)&&(j=p[x[i]+1][y[i]])) edd(i,j,INF);
            if(!(y[i]&1)&&(j=p[x[i]-1][y[i]])) edd(i,j,INF);
            if(j=p[x[i]][y[i]+1]) edd(i,j,INF);
            if(j=p[x[i]][y[i]-1]) edd(i,j,INF);
        }
        if(k==2) edd(i,t,w[i]);
    }
    while(bfs()) ans+=dfs(s,INF);
    cout<<ans<<'\n';return 0;
}