远航序曲
前奏
出发前的稍作准备,复习一部分知识点
KMP的next数组的部分性质:
(以下均默认下标从1开始)
next[i]: 以i结尾的后缀中与其匹配的最大前缀的长度。
对于一个长度为l的字符串s,其最短循环节长度为:l-next[l]
如果\(i\)%\((i-next[i])==0\),那么\(s[1\sim (i-next[i])]\) 为\(s[1\sim i]\)的最小循环元,\(i/(i-next[i])\)为该循环元的循环次数。
树的直径的部分性质
树上任意两点间距离的最大值。(树上任意两节点之间最长的简单路径即为树的「直径」)
求树的直径个人比较喜欢跑dfs(然而不能处理负边权)。
部分性质:
1.一棵树可能有多条直径。
2.直径的两端点一定为叶子节点。
3.对于任意一点而言,树上距离它最远的点一定是直径两端点之一。
4.对于两颗树,其中一颗树的直径端点为\(a\)、\(b\),另一颗树的直径端点为\(c\)、\(d\),用一条边将两颗树连起来,所形成树的直径的端点为\(a\)、\(b\)、\(c\)、\(d\)中的两个点。
5.树上所有边边权均为正,则树的所有直径中点重合
树的重心的部分性质
树上最大的子树节点个数最小的点叫做数的重心。
部分性质:
1.树的重心最多有两个,若有两个,那么这两个重心一定相邻。
2.以树的重心为根时,树上所有子树大小不会超过整颗树的一半。
3.在树上所有点到某点的距离之后中,所有点到重心的距离和最小,若有两个重心,则所有点到它们两个的距离和相等。
4.把两个树通过一条边相连得到一个新的树,那么新的树的重心在连接原来两个树的重心的路径上。
5.把一个树添加或删除一个叶子,那么它的重心最多只移动一条边的距离。
搜索剪枝
回顾下搜索的剪枝:
1.可行性剪枝,当该状态不可能合法时,直接返回。
2.最优性剪枝,如果该状态最终所得结果一定不优于先前做得的结果,直接返回。
3.记忆化搜索。
4.搜索顺序剪枝。 部分情况搜索顺序会较大幅度影响速度,例如从左上跑右下的迷宫图,先跑右下两方向一般优于先跑左上两方向。
有点类似A* ?通过一定条件对各个状态进行估价,根据估价按顺序搜索。
迭代加深搜索
迭代加深一般是对dfs的优化,每次搜索都限制搜索的深度,若未搜到结果,就把深度限制增加,再重新开始搜索。
其搜索方式不是拓展,而是迭代。
本质还是暴力,时间复杂度呈指数级增长。
使用范围:一般当题目搜索树很深,但答案所处深度较浅时使用。
DAY1 7.24
数据结构专场。 出题人:lxl
T1: 考的异或,开始很快写出了暴力,结果发现样例过不了,仔细检查后未发现错误,后面有人反馈说样例错了,样例修改后就过了,考虑数据结构优化,拿线段树稍微优化了下暴力,预计80分,跑路。
实际得分80,正解利用了异或的性质,开个桶存一下就好了。
T2: 敲暴力,暴力完发现可以优化一下,写了个线段树优化。样例过了,预计30-50分。求区间平均值问题,有负数,最终写成分数的形式,还要通分。
实际得分0,不知道哪里挂了。正解是推出的一个性质,最终的答案区间长度不能为1(为1的话就是区间最大值了),所以长度一定为2或3,把一个区间分成两个小区间的话,该区间的平均值一定比两个小区间中平均值较大的那个小。
T3: 先做的T4再做的这题,按照题意暴力模拟,预计20分,最后想到了一个拿另外20分部分分的做法,但时间不够了。
实际得分,20分,正解没听懂,应该是分块,lxl讲的太快了,全程掉线。
T4:暴力模拟收下30分,感觉像图论建模+数据结构优化,想不到怎么优化暴力,去看T3了。
实际得分:30分。题目可以建模出一颗环套树森林,树的部分用树剖搞,环的部分比较好处理。很毒的一点是不能建虚拟节点,每棵树都需要分别树剖。很多地方都只是听了个大概,具体也不太懂。
DAY2 7.25
数据结构优化DP场 出题人:lxl
实际得分:140分。被虐麻了。
T1:签到题,没什么好说的,很快就切了。
T2:与上升子序列有关的统计方案数的题,计数一直是弱项,暴力求方案数想了好久,也想不出怎么用数据结构优化了,预计60分。实际得分40分,原因是因为没看到题目中的\(L<R\),也就是区间长度不能为1。
T2正解是用树状数组记录dp值,所有a[i]都小于等于n,因此不需离散化就能用值域树状数组维护,因为k很小,所以可以开下k个树状数组。开12个树状数组就可以了。
T3: 想了个\(n^3\)的区间DP,一测发现大样例秒过,大样例过水,自己小数据稍微改改就卡死了。
最小数据范围 \(n<=5000\),过不了,希望数据别开满。预计得分:0分。实际得分0分。
T3 正解很复杂,发的std也跟老师讲的不太一样,这里采用lxl讲的做法。
问了老师和同学好几次,可能还是有点糊涂。
一个简单的性质是在确定一个区间的左端点的时候,它的右端点离它越近越好,同理,确定右端点的时候,左端点离它越近越好(区间长度尽可能短)
题意要求的区间不能重叠,将区间看做点后可以建模出一颗树,先处理出区间,对所有区间进行排序,用权值线段树(或者set)维护每个区间的后缀最大值。
处理区间需要开一个last数组和一个pre数组,再开一个next数组将各个区间连成树,用倍增跳树。
计算next数组的时候建一颗存储区间右端点\(y_i\),下标为\(x_i\)的权值线段树,每次把\(y_i\)插到\(x_j\)的位置,计算后缀。
T4: 题目给出了一个很复杂的式子,想不出怎么降维,最后只能模拟题意写了个n^5的暴力,预计得分0分,实际得分0分。
T4有一个拆贡献的思路可以拿50多分。题目给的式子需要枚举区间的左右端点,然后再在区间里枚举i,数据范围太大,需要降循环。
时间主要花在枚举区间上,如果选择先枚举i,那么可以方便的求出区间左右端点,无需枚举区间。用平衡树从1枚举到n,所有的maxpre都加上\(a_i\)后再插入到当前的\(a_i\),然后查询大于零的数的和。 全局加可以打全局标记。 最终时间复杂度能从\(n^5\)降到 \(O(n log n)\)
DAY3 7.26
图论(图)专场 出题人:张致(本来想写zz的,被why吐槽了)
实际得分: 155,本来还以为能200+的。
T1:一眼送分题,数据固定\(4\times 4\),dfs应该能稳过,发现第二组样例慢了,加个最优性剪枝,跑的飞快,自己搓的好几组样例也过了。
实际得分100分,我似乎是唯一一个写dfs的(大概?),出题人的本意好像是状压后跑bfs,\(4\times4\) 的数据可以状压开下(然而很多人不状压bfs也过了)
T2: 一眼最短路,两眼生成树。先敲暴力,根据题意用最小生成树模拟,发现小样例都跑的很慢,考虑优化,加个预处理优化,过小样例,把小样例优化加进循环里,三组大样例全跑的飞快,感觉稳切了,再不济70分也没问题。
实际得分:40,捆绑测试太毒了,发现我的做法和其他人做法又不一样,其他人都是二分答案去二分k,我是选择自己写了个函数暴力加,如果最终的k特别大的话是有办法构造数据卡的,所以可以也用二分优化一下函数。这题还有一点是极限数据卡long long,开int128就稳过了。
T3: 很眼熟的一道题,然而最短路计数没学明白,只能敲暴力了,预计15分。
实际15分,没挂分,正解很妙,求最短路的时候顺便处理当前节点的前缀,如果该节点存在两个前缀满足性质,该节点也满足性质。
T4: 根据题目不嫩看出是二分图,我的第一反应是跑网络流,可能是刻板印象,我一直觉得网络流能实现所有匈牙利算法的功能,然而不会处理区间,最后敲的暴力,预计0分。
实际0分,数据没给暴力机会,出题人说这题跟网络流没任何关系,用网络流可以收获25分的好成绩,加个状压可以收获45分的成绩。正解是用的匈牙利(还是bfs实现的,很难理解),太久没敲了,该复习下了。
考后总结的时候教练建议我们写对拍,做一个题,检查一个题,一定要写对拍,尽量别用手造数据,开始的时候先拍小数据,然后再换大数据。千万别贪多,一定要检查。
DAY4 7.27
图论(树)专场 出题人 Wu_ren (其实就是zz)
T1:签到题,考试开始后出题人发现样例出错后改了题面和样例,如果用的是dfs,大样例会爆掉DEV默认的栈空间,实际交上去不会有问题,以防万一我选择用循环写,因为题中性质,所以可以倒着循环,不自行开栈空间就能过大样例。
实际得分:100,没什么好说的。
T2:一道概率题,外加分数取模。
看数据范围感觉暴力分不好拿,就跳过这个题了。
实际得分:0。根据题目推性质,可以推出一个很好用的性质,最后不需要跑图直接计算就行。
T3:一眼看过去跟树没有什么关系,但有树的部分分,暴力五分敲掉,再敲20分的树情况的暴力,之后想的是这题缩点后图一定变森林,可以跑树,但缩点没法保证一定合法,而且题目需要记录过程,最后没想出解法。
实际得分:25。有一个部分分给的是仙人掌图建圆方树,不会。正解是遍历图的时候建dfs树,建树时没有用到的边标记一下,然后先处理没打标记的边,再处理打标记的边时会发现可以通过调整没打标记的边保证合法。
T4:处理序列的题,还是不太会处理区间建图问题,看有5分的暴力是\(n<=20\),敲的5分暴力。
实际得分:0。挂分原因是部分分只说了\(n\le20\),没规定\(m\),\(m\)依旧可以开满卡死纯暴力。
感觉T2很有意思,再记一下T2吧。
题目描述:
给定$ [1, n] ∩ Z \(的一个子集 S,询问若\) i \(的父亲在\) [1, i − 1] \(中等概率生成,
\)S$ 中的点从上到下形成一条链的概率,\(q\) 次询问。
\(1 ≤ n, q ≤ 3 × 105\),询问的子集大小总和不超过$ 3 × 105$。
解题思路:
先说结论,最后题目会变成求:\(\prod _{i=1}^{m-1} \dfrac{1}{x_i}\)
设\(S\)中的点从小到大依次为 \(x_1,x_2,x_3,x_4......x_m\),那么推出一个神奇的结论:
\(x_i\) 为 \(x_{i+1}\)的祖先的概率一定为\(\dfrac{1}{x_i}\)。
为什么呢?
\(x_i\)和\(x_{i+1}\)不一定是连续的,但我们可以使用归纳法,先从\(i\)和\(i+1\)开始看起。
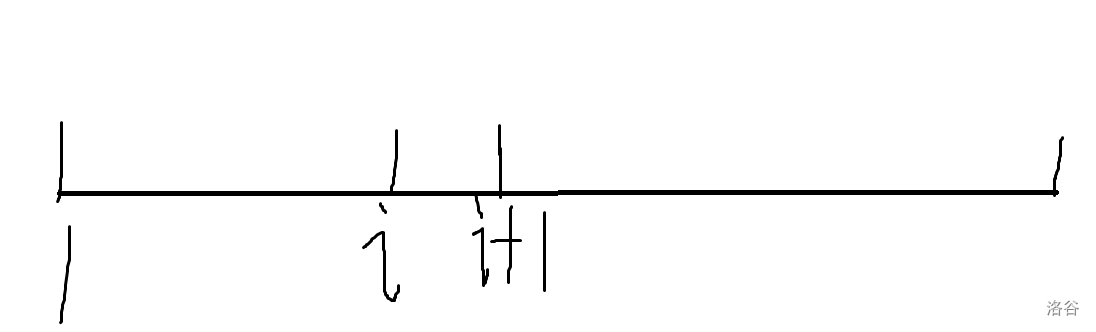
\(i+1\)的父节点只可能在\([1,i]\)之中等概率选一个,如果是\([1,i-1]\)中的任意一个,那么\(i\)就不可能成为\(i+1\)的祖先了。因此\(i\)是\(i+1\)祖先的概率等于\(i\)是\(i+1\)父亲的概率,也就是\(\dfrac{1}{i}\)
再来看看\(i+2\)
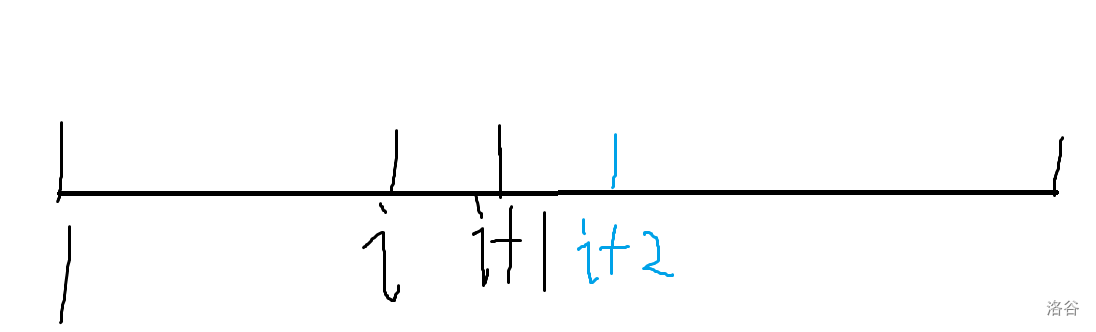
\(i+2\) 的父节点一定在 \([1,i+1]\) 中,其中在 \([1,i]\) 区间里的概率为\(\dfrac{i}{i+1}\),
其中在\([1,i]\)区间里选到\(i\)的概率为\(\dfrac{1}{i}\),因此 \(i+2\) 的父节点为 \(i\) 的概率为 \(\dfrac{i}{i+1} \times \dfrac{1}{i} = \dfrac{1}{i+1}\)。同时,\(i+2\)的父节点为 \(i+1\) 的概率也为\(\dfrac{1}{i+1}\) , \(i+1\)的父节点为 \(i\) 的概率为 \(\dfrac{1}{i}\)
同理,可以推出 \(i+3\) , \(i+4\) , \(i+x\) 的祖先为 \(i\) 的概率都为 \(\dfrac{1}{i}\)
因此\(i+2\)的非父节点祖先为 \(i\) 的概率为 \(\dfrac{1}{i+1} \times \dfrac{1}{i}\)
两者加起来就是 \(i\) 为 \(i+2\) 父节点的概率 \(\dfrac{i}{i+1} + \dfrac{1}{i+1} \times \dfrac{1}{i} = \dfrac{1}{i}\)
因此序列中 \(x_i\) 为 \(x_{i+1}\)的祖先的概率一定为\(\dfrac{1}{x_i}\)。(序列保证了 \(x_i\) 大于 \(x_{i+1}\) )
最终答案就是\(\prod_{1}^{m-1} \dfrac{1}{x_i}\)
DAY5 7.28
DP专场 出题人:zjf
T1: 带点计数类的题,考场没想出正解,写的20分暴力,可能是太久没写的原因,一个bfs废了我半天时间。
正解是一个很简单的DP,考试应该再推推的。
设 \(f[i][j][k][0/1]\) 表示在 \(i,j\) 位置,异或和为 \(k\) ,\(0\) 表示一路上有没有选择扔的方案和。
转移方程:
\(dp[i][j][k][0]\) \(+=\) \(dp[i-1][j][k \text{^} a[i][j]][0]+dp[i][j-1][k\text{^}a[i][j]][0]\)
$dp[i][j][k][1] += dp[i-1][j][k\text{^}a[i][j]][1] + dp[i][j-1][k\text{^}a[i][j]][1] + dp[i-1][j][k][0] + dp[i][j-1][k][0] $
T2: 一眼树形DP,想写正解,先敲的T3暴力,回过头来敲正解的时候写了很久,然后发现题意理解有误,重新敲的时候心态炸了,暴力都调了很久。预计50分。
实际五十分。正解是个理解起来有点麻烦的树形DP,代码实现并不难。
T3:42分暴力比较好拿,敲完就跑路了。预计42分
实际42分,正解竟然是数位DP,题目中的序列可以用数位DP的思想处理。
T4:吸取昨天T4 \(m\)过大的教训,先预处理区间再暴力,结果没调出来。预计0分。
实际0分,正解是决策单调性+斜率优化,不太会。
考后总结:
教练跟我们说搜索最重要的是判重,其次才是剪枝。
考试题目一定要至少读三遍,觉得懂了也要强迫自己读三遍,第一遍看关键词,第二遍细读,第三遍找细节。
考试前一定要重新编译、运行代码,不要随机保存,先保存在桌面上,再复制到文件夹里覆盖。
插曲
紧急作战:补习数学。
GCD:
数论只会GCD。(实际也不会)
辗转相除法:
int gcd(int a,int b) {
if(b==0) return a;
else return gcd(b,a%b);
}
更相减损法(可避免大整数取模导致效率低下,但总体不如辗转相除法):
int gcd(int a,int b){
if(a==b) return a;
if(a>b) return gcd(a-b,b);
if(a<b) return gcd(b-a,a);
}
筛素数:
欧拉筛(线性筛):
for (int i=2;i<=n;++i) {
if (!b[i]) {
d[++t]=i;
}
for (int j=1;j<=t;++j) {
if (i*d[j]>n) break;
b[i*d[j]]=1;
if (i%d[j]==0) break;
}
}
组合数:
$\dbinom{n}{m} $ 表示在 \(n\) 个中选 \(m\) 个的方案数
组合数的计算:
$\dbinom{n}{m} = \dfrac{n!}{m!(n-m)!} $
一点公式:
排列数:
$ \mathrm A_{n}^{m} $ 表示从 \(n\) 个元素中选出 \(m\) 个元素的排列个数。
计算:
全排列(排列数的特殊情况):
DAY6 7.29
数学专场 出题人:zjf
T1:考的筛法,比较裸的题目,感觉埃氏筛更适合解这个题,就用的埃氏筛,自己造数据的时候忘了怎么保证全为质数了,感觉没什么区别,就用的奇数。然后自己测的时候发现跑的很慢,预计能过70分。
实际得分100分,题目保证了测试点全为质数,这会比非质数快很多。
T2:依旧与筛法有关,直接连树绝对会炸。树的深度不会太大,应该可以暴力跳链。根据题意模拟写了个暴力,用的欧拉筛,预计20。
实际得分:20。没挂分。正解和暴力很像,可以在预处理质数的时候顺便处理出各个点的父节点,询问的时候暴力跳链统计答案即可。
T3: 根据题意模拟暴力,预计30分。敲完T4暴力后感觉唯一能优化的点就是这个了。突然想起了yys学长提到过的分段打表,然而学长几乎是只提到了名字,原理和代码实现都没见过。尝试写点东西优化暴力的时候突然悟出了点东西,推测这就是分块打表的原理,然而没实现过,于是手动打表打了一个多小时,最后还是没卡过70分的点。
实际得分:30分。70分的部分分的确可以用分段打表实现,原理也和我理解的差不多,可惜实现上还是疏忽了。完全可以把打表交给程序的,可惜考试时没实现出来。正解是推式子,推到最后能缩成 \(O(n)\) 的复杂度。
T4: 想不出正解,写的暴力。预计25分。
实际25分,正解是容斥。式子比较难推。
不和谐音符
字符串哈希
紧急补习一波字符串。
哈希值的计算:
for (int j=1;j<=size;++j) {
Hash[i]=Hash[i]*base+ch[j]-'a'+1;
Hash[i]%=Mod;
}
DAY7 7.30
字符串专场 出题人:zzz(张尊喆)
真,啥也不会。讨论了一波题,没时间记了,少记一点吧。
T1 50分暴力拿好,用倒退就是满分。
T2: 乱搞拿了5分。
T3: 不会。
T4: 博弈题,很有意思,但考试时0分。
总分:55分,来这里以来我拿的最低分。
赛后和cjx和yzy讨论的时候讨论的有些激烈,讨论了好久,最后我似乎悟出了好像在某个博客看到
过的min-max搜索。
之后问老师的时候得知这个确实是min-max搜索。
DAY8 7.31
动态规划+图论专场 出题人:(张尊喆)
T1:一眼看过去没有暴力分,想了一下发现50分部分分还是很好拿的,调了一段时间后调出了暴力,以各个节点为根跑n遍树形DP,肯定拿不了全分,特判一下50分部分分,只跑一边dfs。然后就看后面了。之后回来写的正解,想到一个换根DP的做法,跑两遍dfs,但在实现上花了很长一段时间。最后来不及对拍了,看着样例都能过就交上去了。预计100分。
实际:75分。dp式子还是有点问题。正解没有这么麻烦,dp上和我的想法基本一致,但只需要维护最大值和次大值就行了。实现也很简单(赛后听同学说这个类似树的直径)。
T2:只有一个80分的阶段分,估计不会放过暴力,估计正解用拓扑实现,但想不出来,最后交了个n遍dfs的暴力。预计0分。
实际0分。正解用了bitset,以前用过bitset的另一种用法,现在才知道bitset还可以实现布尔数组的一些功能,bitset数组有一个.count(),可以输出数组里1的个数,很方便,算长见识了。
T3:30分暴力比较好拿,但没怎么用过vector,这次调代码的时候被这个卡了很久,写完暴力后感觉还可以随机化乱搞一下,不过时间已经不太够了,看T4。
正解用到二分答案,二分mid,判断是否有合法方案的根节点的值是否可以大于等于mid。
设\(f[x]\)表示最少在x的子树内分配多少个大于等于mid的叶子节点,使得x的权值大于d等于mid
那么选择 \(k/2\) 个叶子节点,那么 $ f[x]=\sum f[y] $,所以将儿子按照 $ f[x] $ 排序,从小到大选择,最终判断$ f[x] $ ,是否小于等于可分配的叶子权值个数。
T4:题目读完后感觉不好暴力,有个30分部分分应该是个比较简单的数学计算,可惜我数学太差,没看出这就是个第二类斯特林数(估计看出来也不会实现)
正解:考虑从上往下分配集合,(也可以按照dfs序排序),保证祖先在自己之前分配集合,那么有:
这表示放到之前的集合内(不能与祖先放在一起,其他集合随便放),或者自己新建一个集合的方案。
赛后发现去年夏令营给我们讲课的张华清老师在赛时也交了T4,用的一个很奇怪的做法,问了一下讲课老师,老师说这是用的二项式反演,原做法是的\(f[x][y]\)是不和自己祖先放一起的方案,而这个做法则是不考虑有没有和祖先放在一起,利用二项式反演+容斥求答案,时间复杂度上是一样的。
DAY9 8.1
搜索专场 出题人:袁神(袁浩天)
T1: 先用搜索枚举各个未知数的值,然后根据字符串模拟加减乘运算(会有小括号),因为对自己的模拟水平没信心,外加第一次用在考场上map,开始T1写一半就选择先放弃看后面的,在最后做的T1。预计100分。
实际100分。
T2:搜索+剪枝题,第二个样例开满了,没过,手搓样例不能保证一定有解,预计能过40分到60分。
实际得分:0分。原因是多次的时候忘清零标记了。正解其实只需要在我的做法基础上改一下搜索顺序,倒着搜就过了。(写正解的时候忘记加自己一开始的一个剪枝,结果和yzy调了一晚上)
T3: 有限状态自动机?看不懂题目描述。 题目描述有种lxl的题目背景的美。实在看不懂题意,样例也莫名奇妙的。跳过不做了。
正解是构造有向图,整体搜索一个一个加点,搜索连边考虑剪掉不用的状态,最后可发现只在 \(n<=4\) 的情况有解,限制上界边界为4可有效加快运行速度。
T4: 发现60分的部分分可以打表,打了一段时间的表,然后去做T1了。预计60分。
实际得分:60.正解就是打表,用的更优秀的搜索打表。
考后总结:
1.多测记得清空
2.造数据一定要练
3.考试样例不可信,过了也要自己造数据。一定要对拍,一定要对拍。
4.调试程序建议用gdb,比DEV要好用很多。
DAY10 8.2
数据结构+图论专场 出题人:yht
T1:开始的时候先敲一个广搜暴力,调了好几下后过了小样例。之后考虑正解,一个比较简单的最短路题,写完对拍时发现暴力似乎还有点问题,正解应该写对了,预计100分。
实际100分,正解与所想一样。
T2: 暴力敲完,正解想不出来,看T3了。预计得分:30分。
实际得分:30分,人太菜了,70分DP做法没看出来。正解是线段树+扫描线。
T3: 暴力分拿好,后面的部分分想不出来了,看下一题。预计得分:40分。
实际得分:40分。正解用的容斥+莫队,不会莫队。
T4: 依旧只会暴力,预计20分。
实际:20分。 可以发现两点间距离的中点很重要,这个中点可能会出现在边上,也有可能出现在点上,出现在点上的情况比较好处理,如果出现在边上则不方便处理,因此考虑对每个边进行扩建。一个技巧就是在每条边上新建一个点。之后就是推性质+背包DP计数,最后两遍dfs统计答案。
考后总结:
1.造数据造联通图的时候,可以先造树,再在树上随机加边。
2.莫队注意分块大小,不一定根号n就是最优答案。
3.调试记得删完。
DAY11 8.3
全真模拟场 出题人:朱羿恺
T1: 先写的30分暴力,然后去做的后面的暴力,回过头来又写了一个70分的暴力,之后考虑正解,想到一个感觉没问题的解法,但没过大样例,没敢交。预计70分。
赛后提交了一下没调出来的代码,发现能90,加个只选一种的特判就满分了,但还是过不了大样例。经过跟同学讨论和问老师后,发现我的思路与正解相比还是有些问题。
T2: 写的暴力,预计20分。
实际20分。正解是DP。
T3: 暴力有些问题,没调出来,先看的后头,后来感觉T1更好想就把时间都给T1了。
实际0分。正解是DP
T4: 写的暴力,预计12分。
实际12分。正解是推性质,然后线段树维护后缀最大值。
DAY12 8.4
全真模拟场 出题人:朱羿恺
T1:先写了个暴力,然后看的后面的题。之后回过头来写个了线段树优化,预计100分。
实际得分:100。 正解是差分,不过线段树也能过就是了。(似乎在洛谷上有一道很相像的题)
T2:额,前几天考过的原题?不过原题我似乎还是不太会做。写完暴力后补了个小优化,预计50分。
实际得分:50分。太菜了,前几天的看来还没掌握好,需要再练练。
T3;只会个30分暴力。
实际得分30分。正解是推性质。
T4:暴力枚举的所有子集,预计30分。
实际得分30分。正解是状压。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号