【笔记】博弈论
教练让我学三周数论，然而数论多少还是无聊了点，所以浅学一下博弈论划划水。
（只是简单学了一下，不会记特别多。）
何为博弈论？
博弈论 ，是经济学的一个分支，主要研究具有竞争或对抗性质的对象，在一定规则下产生的各种行为。博弈论考虑游戏中的个体的预测行为和实际行为，并研究它们的优化策略。 ---百度百科。
一如既往没什么用的定义。
博弈图
抽象的定义显然不适合我们做题，所以我们可以试试把问题转化为图。
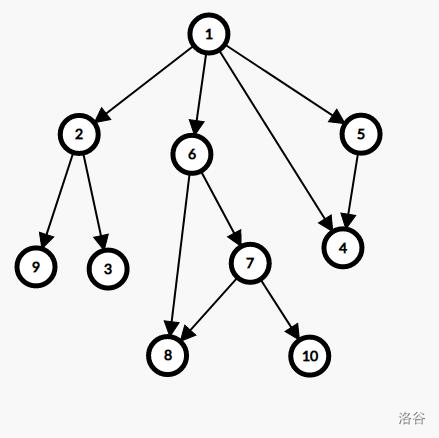
我们将每一种可能到达的状态看做一个节点，每次决策都是从旧状态转移到新状态的过程，在两个状态之间连一条有向边，如果把所有状态转移都画出来，我们就得到了一张博弈图。
例如这张：
组合游戏：
平等组合游戏（\(ICG\)）：
定义：
1.游戏有两个人参与，二者轮流做出决策，双方均知道游戏的完整信息；
2.任意一个游戏者在某一确定状态可以作出的决策集合只与当前的状态有关，而与游戏者无关；
3.游戏中的同一个状态不可能多次抵达，游戏以玩家无法行动为结束，且游戏一定会在有限步后以非平局结束。
有向图游戏
所有的\(ICG\)转换成博弈图的话一定是一张\(DAG\)图（有向无环图）
所有的\(ICG\)都可以抽象成一个游戏：
给出一张\(DAG\)，在给定起点处有一枚棋子，两人轮流移动棋子，如果谁不能移动了就判输。
必胜态和必败态：
必胜状态，即决策前处于这种状态的人必胜。
必败状态，即决策前处于这种状态的人必败。
三个小定理：
-
没有后继状态的状态是必败状态
-
一个状态是必胜状态 当且仅当 存在至少一个必败状态为它的后继状态。
-
一个状态是必败状态 当且仅当 它的所有后继状态均为必胜状态。
对于定理一，一个状态没有后继状态，说明一个人这一状态时无法继续决策了，这个人也就输了。
对于定理二，小A决策后状态变为\(N\)，小\(B\)再决策时只能从状态\(N\)走向一个必败状态，此时小A就赢了，状态\(N\)就是一个必胜状态。
对于定理三，小A决策后状态变为\(P\),小B再决策时可以走向一个必胜状态，这样小A就输了，状态\(P\)就是一个必败状态。
面对一个\(ICG\)问题，博弈图是一个\(DAG\)。在绘制出博弈图后，我们可以使用拓扑排序，在\(O(n+m)\)（n为状态数，m为边数）的时间内求出每个状态是必胜状态还是必败状态。
经典的公平组合游戏
巴什博弈：
有两个聪明人玩游戏，有n个石子，两人轮流从这堆石子里取出一部分，每人一次可以取[1,m]个石子，最后不能拿的人输。两人都会选择最优策略的情况下，问：先手和后手谁赢？
当\(n<=m\)时，先手可以一次拿走所有的，先手胜。
当$n=m+1 $时， 无论先手怎么拿，后手都可以一次拿走所有的，后手胜。
当\(n=k*(m+1)\) $ $ $k\in Z $ 时,对于每个\(m+1\)个石子，先手取\(x\)个，后手一定可以一次将剩下的\(m+1-x\)个石子全部取走，后手胜。
当\(n=k*(m+1)+x\)且\(0<x<m+1\)时，先手第一步取走x个石子，接下来变成上一种情况，先手胜。
结论：
当n不能整除m+1时先手必定胜，能整除时后手必胜。
nim游戏：
nim游戏是对巴什博弈的升级。
有两个聪明人玩游戏，有\(n\)堆石子，第\(i\)堆有\(a[i]\)个，两人轮流取石子，每次每人可以选择一堆取任意多个石子，最后不能取的人输。两人都选择最优策略的情况下，问:先手和后手谁赢？
当\(n=1\)时，先手的人可以一次拿完，先手胜。
当\(n=2\)且\(a_1==a_2\)时,先手无论从一堆里取多少个，后手都可以选择在另一堆里取同样多个，最后后手胜。
当\(n=2\)且\(a_1!=a_2\)时,先手先在较多的那堆里取走\(|a_1-a_2|\)个，变成上一种情况。后手无论从一堆里取多少个，先手都可以再从另一堆里取同样多个，因此先手胜。
分析\(n=2\)时的两种情况，我们可以发现一个非常有用的策略，即选择在另一堆里取和对方相同数量的石子，而当两堆石子数量相同时，\(a_1\)和\(a_2\)的异或和为\(0\)
当\(n>=3\) 时，情况变得复杂了起来。
先说结论：当\(a_1\)^ \(a_2\)^ \(a_3\)^\(……\) ^ \(a_n=0\)时，先手必败，反之先手必胜。
假设现在的局势时\(a_1\)^ \(a_2\)^ \(a_3\)^\(……\) ^ \(a_n=0\)，先手选择其中一堆，取k个石子。
局势就变成了\(a_1\)^ \(a_2\)^ \(a_3\)^\(……\) ^ \(a_n=k\),也可以写成\(a_1\)^ \(a_2\)^ \(a_3\)^\(……\) ^ \(a_n\)^\(k\) \(=0\)
设\(k\)二进制的最高位1在第\(x\)位，此时一定有奇数个 \(a_j\)二进制的第\(x\)位为1
此时后手选择其中一个\(a_j\)从中取出\(a_j\) ^ \(k\)个石子，使全局的异或和再次变成\(0\)，重复上述操作，后手一定能将局势变成：\(n=2\)且\(a_1==a_2\)的情况，后手必胜。
以后再记。
