【笔记】线段树优化建图
正常情况下,我们给两个点连m条边,时间复杂度为\(O(m)\)
当一个点给长度为n的区间内的每个点连m条边时,时间复杂度就变成了\(O(n*m)\)
当一个长度为n的区间内的每个点向另一个长度为n的区间内的每个点连m条边时,时间复杂度就变成了\(O(n^2 *m^2)\)
显然,这样连边效率很低,这时候就可以使用线段树对连边进行优化。
线段树连边的思想与网络流的拆点思路类似。
对于一颗线段树,从父节点向子节点连边,这样我们只需要连向所属区间的点的父节点就能实现对整个区间的连边
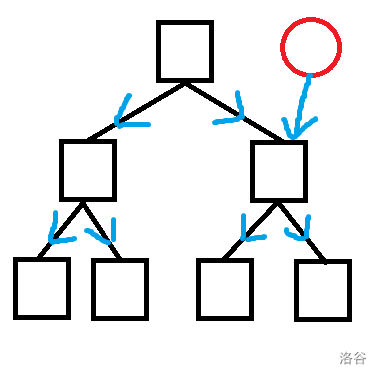
根据这个原理,我们可以构建如下模型:
将图上的每个节点拆成出点和入点两个点,在出点和入点上分别建一颗线段树,记作出树和入树。
出树处理出边,边的方向由父节点指向子节点。
入树处理入边,边的方向由子节点指向父节点。
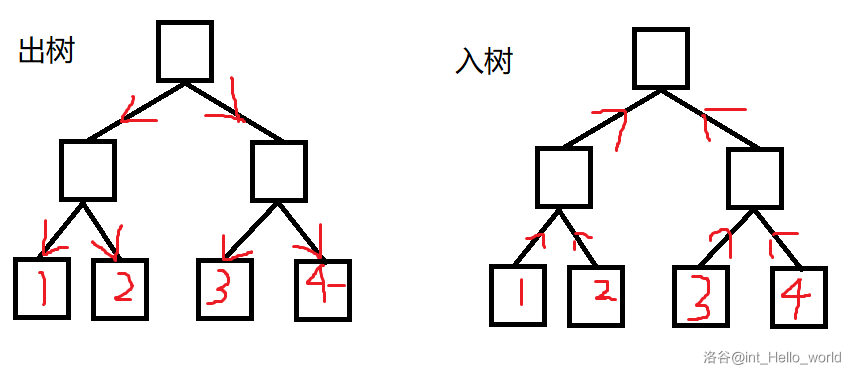
再给每个节点对应的出入点之间连一条边,由出点指向入点。
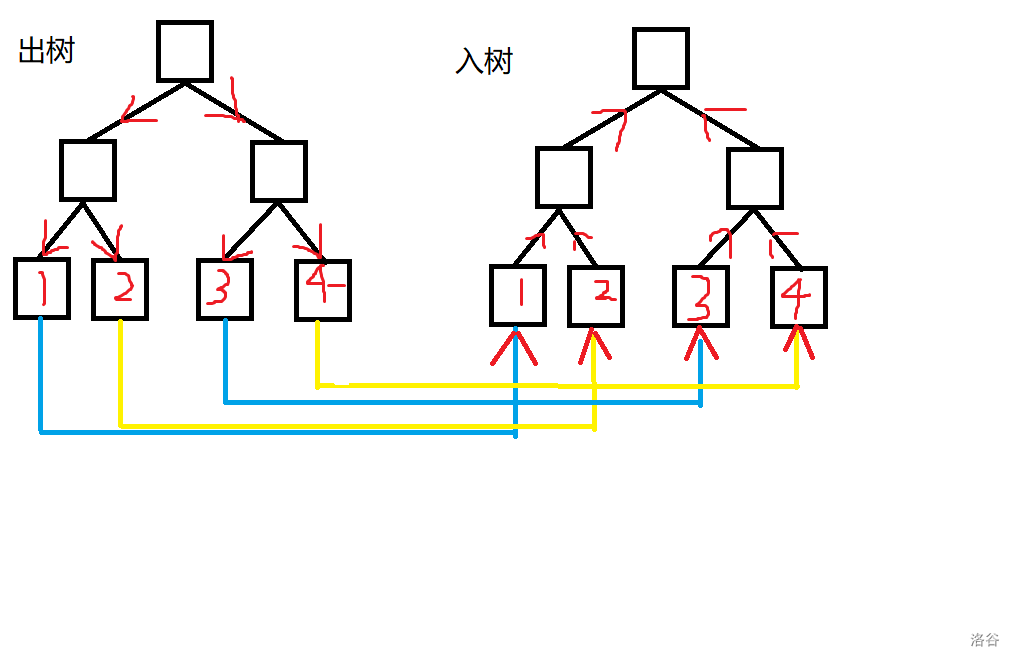
模型建完了,剩下的就是连边了。
操作一:单点向区间连边
假设现在让1号节点向2-4区间内的所有点连一条边,那么只需要将1号节点的入点连向该区间内叶子节点的父节点的出点即可。
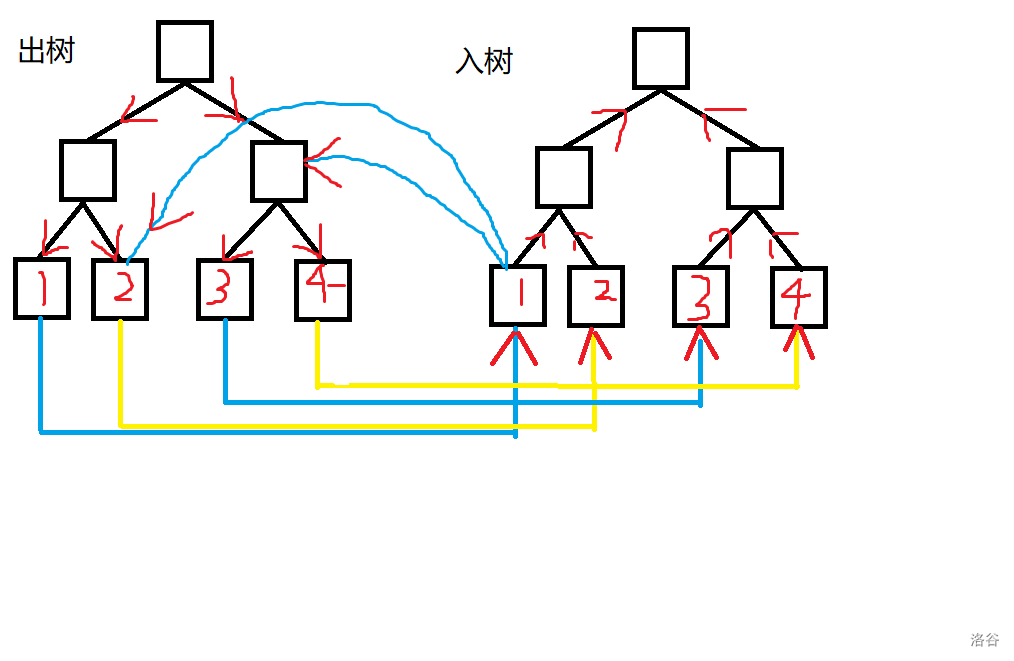
可以看到从节点1的入点出发可以到达节点2-4的出点
操作二:区间向单点连边
假设现在让区间2-4内的所有节点向节点1连一条边,那么只需要将该区间内叶子结点的父节点的入点连向1号节点的出点即可。
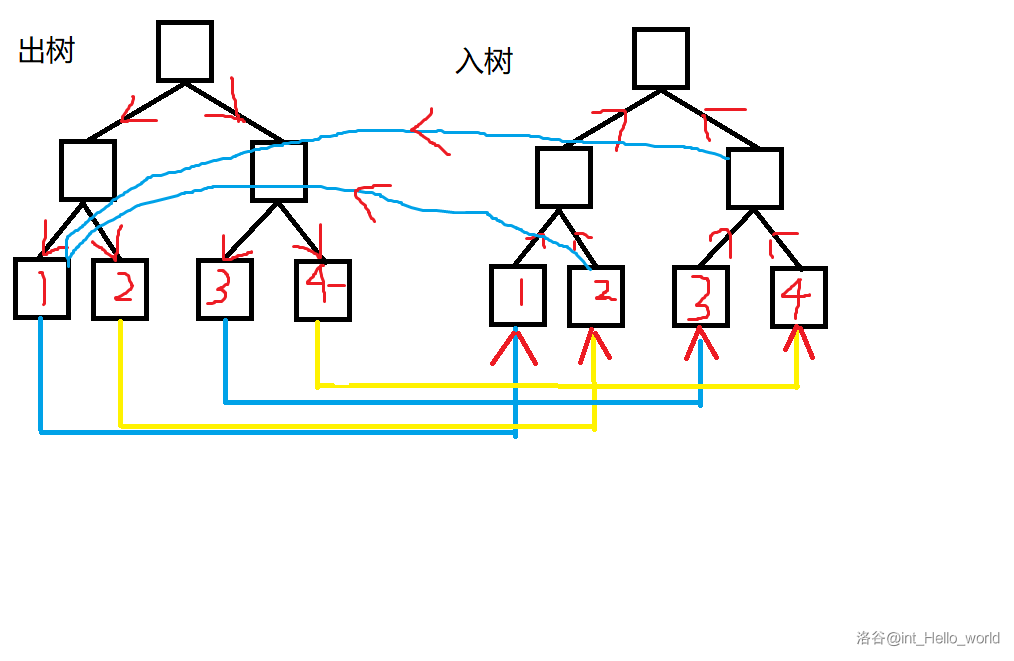
可以看到从区间2-4内任意节点的入点都可到达1号节点的出点。
操作三:区间向区间连边
(图以后再做,咕)
找出两颗树的对应节点从入树向出树暴力连边?但这样的话空间复杂度会变成\(O(nlog_2^2n)\),有待优化,
考虑每次建边时建一个虚点,连边变成入树对应点->虚点->出树对应点,时间复杂度会优化成\(O(nlog_2n)\)。
例题:
CF786B Legacy (板子题,但少了区间连区间这个操作)
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read() {
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
return f?-x:x;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+48);
}
const int N=1e6+2023;
int x,y,z,n,m,a[N],k,dis[N],s;
int head[N*5],cnt,tot;
int in_root,out_root;
int in_num[N];//存入树的叶子节点编号
int out_num[N];//存出树的叶子节点编号
const int inf=0x3f3f3f3f3f3f3f3f;
bool vis[N];
struct node{
int next,to,w;
}e[N*5];
void add(int u,int v,int w) {
e[++cnt].next=head[u];
e[cnt].to=v;
e[cnt].w=w;
head[u]=cnt;
}
namespace ss{ //入树
#define lson tree[pos].ls
#define rson tree[pos].rs
struct sss{
int sum,ls,rs;
}tree[N];
void build(int &pos,int l,int r) {
pos=++tot;
if (l==r) {
in_num[l]=pos;
return ;
}
int mid=l+r>>1;
build(lson,l,mid); build(rson,mid+1,r);
add(lson,pos,0); add(rson,pos,0);
}
void update(int pos,int l,int r,int L,int R,int k,int val) {
if (l>=L && r<=R) {
add(pos,k,val);
return ;
}
int mid=l+r>>1;
if (L<=mid) update(lson,l,mid,L,R,k,val);
if (R>mid) update(rson,mid+1,r,L,R,k,val);
}
}
namespace ss2{ //出树
#define lson tree[pos].ls
#define rson tree[pos].rs
struct sss{
int sum,ls,rs;
}tree[N];
void build(int &pos,int l,int r) {
pos=++tot;
if (l==r) {
out_num[l]=pos;
return ;
}
int mid=l+r>>1;
build(lson,l,mid); build(rson,mid+1,r);
add(pos,lson,0); add(pos,rson,0);
}
void update(int pos,int l,int r,int L,int R,int k,int val) {
if (l>=L && r<=R) {
add(k,pos,val);
return ;
}
int mid=l+r>>1;
if (L<=mid) update(lson,l,mid,L,R,k,val);
if (R>mid) update(rson,mid+1,r,L,R,k,val);
}
}
void dj() { //最短路
s=in_num[s];
memset(dis,0x3f,sizeof(dis));
priority_queue<int,vector<pair<int,int> >,greater<pair<int,int> > >q;
q.push(make_pair(0,s));
dis[s]=0;
while(!q.empty()) {
int now=q.top().second; q.pop();
if (vis[now]) continue;
vis[now]=1;
for (int i=head[now];i;i=e[i].next) {
if (dis[e[i].to]>dis[now]+e[i].w) {
dis[e[i].to]=dis[now]+e[i].w;
q.push(make_pair(dis[e[i].to],e[i].to));
}
}
}
}
signed main(){
n=read(); m=read(); s=read();
ss::build(in_root,1,n); //建入树
ss2::build(out_root,1,n);//建出树
for (int i=1;i<=n;++i) { //出入点连边
add(in_num[i],out_num[i],0);
add(out_num[i],in_num[i],0);
}
for (int i=1;i<=m;++i) {
int op=read();
if (op==1) {
x=read(); y=read(); z=read();
add(in_num[x],out_num[y],z); //正常的两点连边
}
else if (op==2) {
x=read();
int l=read(),r=read(),val=read();
ss2::update(out_root,1,n,l,r,in_num[x],val);//点连区间
//在出树上找到该区间后连一条in_num[x]到该区间的边
}
else if (op==3) {
x=read();
int l=read(),r=read(),val=read();
ss::update(in_root,1,n,l,r,out_num[x],val);//区间连点
//在入树上找到该区间后连一条该区间到out_num[x]的边
}
}
dj();
for (int i=1;i<=n;++i) { //输出
if (dis[out_num[i]]==inf) cout<<"-1 ";
else cout<<dis[out_num[i]]<<" ";
}
return 0;
}
[PA2011]Journeys 区间连区间


 浙公网安备 33010602011771号
浙公网安备 33010602011771号