【笔记】浅谈启发式搜索
最近浅学了下启发式搜索，故而记此笔记。
定义：
启发式搜索(Heuristically Search)又称为有信息搜索(Informed Search)，它是利用问题拥有的启发信息来引导搜索，达到减少搜索范围、降低问题复杂度的目的，这种利用启发信息的搜索过程称为启发式搜索。
---------百度百科
启发式搜索（英文：heuristic search）是一种在普通搜索算法的基础上引入了启发式函数的搜索算法。
启发式函数的作用是基于已有的信息对搜索的每一个分支选择都做估价，进而选择分支。简单来说，启发式搜索就是对取和不取都做分析，从中选取更优解或删去无效解。
----------OI Wiki
不得不说，其定义过于抽象。
说直白点，启发式搜索就是开个函数对暴搜进行剪枝。
我们称这个函数为估价函数。
估价函数：
估价函数是通过题目中的启发式信息来评估节点价值的函数。
启发式函数的一般形式为：
$ f(x) = g(x)+h(x) $
其中，g(x)为初始节点到当前节点x的实际代价，h(x)为从x到目标节点的估计代价。估价的核心就在h(x)上
启发式搜索的过程中，会优先搜索价值大的节点，从而更快到达目标节点。
启发式搜索算法中的h(x)函数非常关键，如果定义不当，则不一定能找到最优解。
搜索过程：
说到底，启发式搜索就是搜索的一种剪枝。那么，它的剪枝能力有多强呢？做了张图来模拟下其搜索过程（图略丑，希望能看懂吧）
以广搜为例，来对比下它与暴搜的区别。
普通搜索过程：
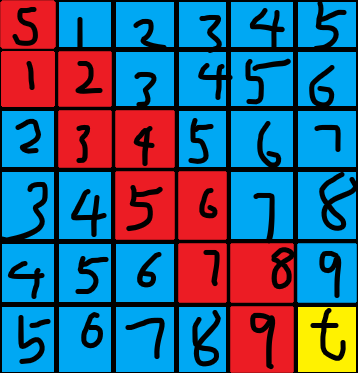
寻找从s到t的最优路径，图中数字为搜索步数，红色部分为从S到T的最优路径，而蓝色部分为无用搜索。
启发式搜索：
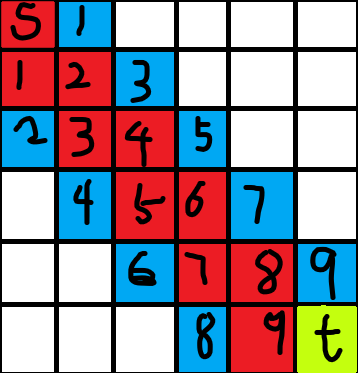
剪枝效果还是很明显的。
例题：
考虑到启发式搜索的定义过于抽象，这里选了一道经典的例题：
[NOIP2005 普及组] 采药
题目描述
辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”
如果你是辰辰，你能完成这个任务吗？
输入格式
第一行有 \(2\) 个整数 \(T\)（\(1 \le T \le 1000\)）和 \(M\)（\(1 \le M \le 100\)），用一个空格隔开，\(T\) 代表总共能够用来采药的时间，\(M\) 代表山洞里的草药的数目。
接下来的 \(M\) 行每行包括两个在 \(1\) 到 \(100\) 之间（包括 \(1\) 和 \(100\)）的整数，分别表示采摘某株草药的时间和这株草药的价值。
输出格式
输出在规定的时间内可以采到的草药的最大总价值。
样例 #1
样例输入 #1
70 3
71 100
69 1
1 2
样例输出 #1
3
提示
【数据范围】
- 对于 \(30\%\) 的数据，\(M \le 10\)；
- 对于全部的数据，\(M \le 100\)。
这是一道非常经典的DP题，也是初学启发式搜索的好题。
抛开启发式不谈，来看最基础的爆搜：
枚举当前为第X个物品，分选或不选两种状态进行搜索，其复杂度为:\(2^n\),显然超时.
进行启发式搜索，构造估值函数：
h(x)=当前时间下，剩余物品能获取的最大价值。
g(x)=目前已经获取的价值。
f(x)：
在不取的时候判断一下不取这个时，剩下的药所能获取的价值和\(h(x)\) + 已经获取的价值\(g(x)\)是否大于目前找到的最优解（最优性剪枝）。当h(x)+g(x)>目前找到的最优解时 才有继续搜索的必要。
取的时候判断一下是不是超过了规定体积（可行性剪枝）,若未超过，则继续搜索。
代码如下：
#include<bits/stdc++.h>
using namespace std;
int ans,n,m;
struct node{
int val,cost;
double sum; //每个物品的估值
}e[1023131];
bool cmp(node a,node b) {
return a.sum>b.sum;
}
int h(int now,int T) {
int tot=0;
for (int i=1;now+i<=n;++i) {
if (T>=e[now+i].cost) {
T-=e[now+i].cost;
tot+=e[now+i].val;
}
else return int(tot+T*e[now+i].sum);
}
return tot;
}
void dfs(int now,int T,int V) {
ans=max(ans,V);
if (now>n) return ;
if (V+h(now,T)>ans) { //g(x)+h(x)>目前找到的最优解
dfs(now+1,T,V);
}
if (T-e[now].cost>=0){
dfs(now+1,T-e[now].cost,V+e[now].val);
}
}
signed main(){
cin>>m>>n;
for (int i=1;i<=n;++i) {
cin>>e[i].cost>>e[i].val;
e[i].sum=(double)e[i].val/e[i].cost*1.0; //每个物品的估值=价值/花费时间
}
sort(e+1,e+1+n,cmp); //为方便剪枝，根据各个物品的估值进行排序
dfs(1,m,0);
cout<<ans;
return 0;
}
