【笔记】随机化算法----从入门到入坟
注:本博客所介绍的算法主要还是用来在信竞考试中骗分的,想了解正经的随机化算法还请另寻他处
碎碎念:
说起随机化算法,我们通常会第一时间想起神奇的模拟退火,然后进入以下流程:
想学一下准备骗分 -----> 看不懂定义 -----> 直接看代码 -----> 代码背不过、参数调不出、样例过不了 -----> 放弃
-----------------------------------------------------------------------------------
随机化算法的主要用途还是解决NP问题,这些算法大部分就是为了解决复杂度难以控制的NP问题而发明的。不过,用来骗分也不失为一种选择。
随机化算法的核心函数:
rand() 输出随机数
srand(2131) 换个随机数种子,初始默认为1,开始时可以调一调种子,防止有些人专门去卡srand(1)的参数。
while(double(clock())/CLOCKS_PER_SEC<0.96 ) 算法函数(); 经典操作,在时间允许的情况下多跑几遍随机化算法提高正确率。
-----------------------------------------------------------
所有的随机算法基本都分为两个模块:计算模块和判断模块。
计算模块因题目而异,随机算法计算模块基本一致的,唯一的不同在于判断模块上。
后面会详细展开,这里就不过多赘述了。
随机化算法常常会用到的一个技巧:随机排序。
随机排序这一技巧有时单拎出来就能解题
随机排序:
随机排序,思想类似于猴子排序。
对一个数列进行随机的排序,然后判断该数列的结果是否为目前最优解。
随机排序的使用条件:
已经获得了一个数列,且最优解与数列排序有关,当数列长度比较小时,可以使用随机排序。
优点:思路和代码都非常简单
缺点:能用的场景太少
例题:
洛谷P2210 Haywire
https://www.luogu.com.cn/problem/P2210
代码:
#include<bits/stdc++.h> #define int long long using namespace std; inline int read() { int x=0,f=0;char ch=getchar(); for(;!isdigit(ch);ch=getchar()) f|=(ch=='-'); for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48); return f?-x:x; } void print(int x) { if(x<0) putchar('-'),x=-x; if(x>9) print(x/10); putchar(x%10+48); } bool vis[101]; int id[102],sum[102]; int x,ans,n,m,a[1023313],b[112311],c[103131]; void S_dfs(){ x=rand()%n+1; memset(vis,0,sizeof(vis)); for (int i=1;i<=n;++i) { while(vis[x]) x=rand()%n+1; vis[x]=1; sum[i]=x; id[x]=i; } int ansnow=0; for (int i=1;i<=n;++i) { ansnow+=abs(id[a[sum[i]]]-i); ansnow+=abs(id[b[sum[i]]]-i); ansnow+=abs(id[c[sum[i]]]-i); } ans=min(ans,ansnow); } signed main(){ n=read(); for (int i=1;i<=n;++i) { a[i]=read(); b[i]=read(); c[i]=read(); } ans=0x7fffffff; while(double(clock())/CLOCKS_PER_SEC<0.96){ S_dfs(); } cout<<ans/2; return 0; }
----------------------------------------------------
各类随机化算法----------以下是,幻想时间。
最朴素的随机搜索:
多次搜索,搜索到时间上限为止,生成出多组可行解,从这几组可行解里找最有解。
从其他博客找的:它只适用于代价函数在值域范围内没有任何变化规律的情况。即找不到任何使得代价下降的梯度和极小值点。
例题:无,反正我是没见过。
当一个题目水到连这种方法都能过的时候,我可能会选择直接“不可以,总司令”。
爬山算法和模拟退火的思路其实是一样的,做了张图方便理解:
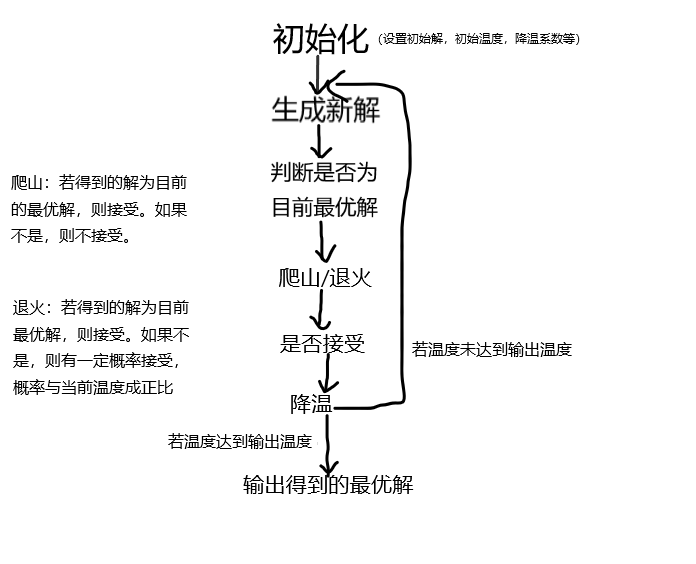
爬山算法---------------承上启下
爬山算法是对于搜索的一种贪心优化。当得到的一组解优于当前的解时,则接受当前解,否则就不接受。
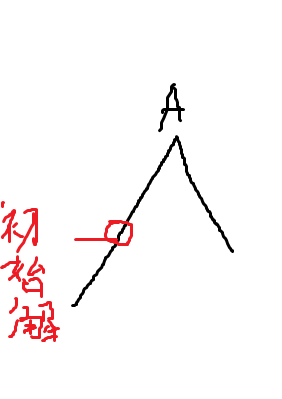
求解的过程就像爬山一样一步一步往上爬,当爬到山顶A的时候,发现相邻的点都比A低,于是A点就成可求得的最终解。
爬山算法是一步一步找到最优解的过程,只会判断与当前解相邻的解是否为最优解,因此可能会出现一下情况:

可以看到,B点为全局最优解,但因为A是目前最优解,爬山算法只会判断A点周围的解来进行更新,所以无法求出最优解。
总结一下爬山算法的优势:代码比退火简单,处理单峰值问题会比模拟退火稳定。
缺点:难以处理结果峰值较多的情况。
而且,爬山算法的题目.........
多少是沾点玄学的。
例题:
洛谷P4035
P4035 [JSOI2008]球形空间产生器 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
因为本题的答案峰值非常密集,所以就给了爬山算法一些机会。
代码:
#include<bits/stdc++.h> using namespace std; inline int read() { int x=0,f=0;char ch=getchar(); for(;!isdigit(ch);ch=getchar()) f|=(ch=='-'); for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48); return f?-x:x; } void print(int x) { if(x<0) putchar('-'),x=-x; if(x>9) print(x/10); putchar(x%10+48); } int n,m; double change[191],Dis[1021]; struct node{ double s[102]; }e[102],ans; double dis(int x){ double w=0; for (int i=1;i<=n;++i) { w+=((ans.s[i]-e[x].s[i])*(ans.s[i]-e[x].s[i])); } return sqrt(w); } void SD(){ double sum=0; for (int i=1;i<=n+1;++i) { change[i]=0; Dis[i]=dis(i); sum+=Dis[i]; } sum/=(n+1); for (int i=1;i<=n+1;++i) { for (int j=1;j<=n;++j) { change[j]+=(Dis[i]-sum)*(e[i].s[j]-ans.s[j])/sum; } } } signed main(){ cin>>n; for (int i=1;i<=n+1;++i) { for (int j=1;j<=n;++j) { cin>>e[i].s[j]; ans.s[j]+=e[i].s[j]; } } for (int i=1;i<=n;++i) { ans.s[i]/=(n+1); } double T=2000; while(T>1e-4&&double(clock())/CLOCKS_PER_SEC<0.995) { SD(); for (int i=1;i<=n;++i) { ans.s[i]+=change[i]*T; } T*=0.99999; } for (int i=1;i<=n;++i) { printf("%.3lf ",ans.s[i]); } return 0; }
模拟退火--------------------调参调到上火:
模拟退火可以说是在爬山基础上的一些改进,可以避免陷入局部最优解的问题。
当得到的解不是目前最优解时,依旧会有一定概率接受这个解,随着时间推移,接受非最优解的概率逐渐减小。
一张非常经典且形象的GIF图:
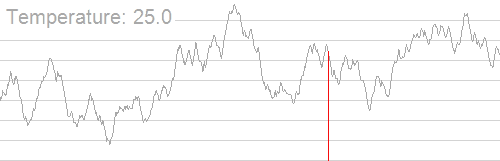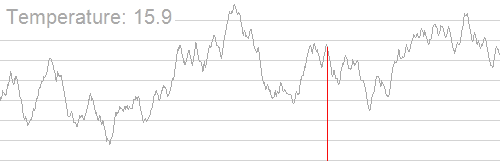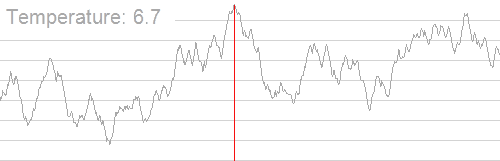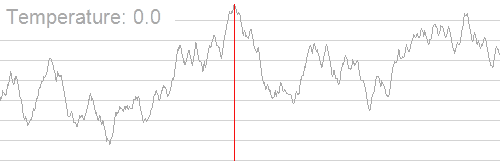
说到底,模拟退火就是多了个在接受答案的时候有一定概率接受非当前最优解,其余按照题目来即可。
因为模拟退火可能会接受非当前最优解的特性,求答案的时候可以跳出当前最优解,也有可能从最优解跳到非最优解,因此模拟退火的代码常常需要我们调整出一个适合题目的参数来提高正确率。
模拟退火在处理单峰值问题时稳定性未必好于爬山算法,但因为不会陷入局部最优解,应用域更为广泛
例题:
洛谷P1337
代码:
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
return f?-x:x;
}
void print(int x) {
if (x<0) putchar('-'),x=-x;
if (x>9) print(x/10);
putchar(x%10+48);
}
int n,m,T_T;
double x[1023131],y[1023313],ansx,ansy,ans,lx,ly,nx,ny,w[10231313];
double query(double ax,double ay,double bx,double by) {
return sqrt((ax-bx)*(ax-bx)+(ay-by)*(ay-by));
}
double calc(double a,double b) {
double res=0.0;
for (int i=1;i<=n;++i) {
res+=w[i]*query(a,b,x[i],y[i]);
}
return res;
}
void SA(){
double T=2022;
while(T>1e-12) {
double nx=lx+((rand()<<1)-RAND_MAX)*T;
double ny=ly+((rand()<<1)-RAND_MAX)*T;
double E=calc(nx,ny);
double del=E-ans;
if (del<0) {
ans=E;
lx=ansx=nx;
ly=ansy=ny;
}
else if (exp(-del/T)>double(rand())/RAND_MAX) {
lx=nx;
ly=ny;
}
T*=0.996;
}
}
signed main() {
n=read();
for (int i=1;i<=n;++i) {
scanf("%lf%lf%lf",&x[i],&y[i],&w[i]);
lx+=x[i];
ly+=y[i];
}
lx/=double(n);
ly/=double(n);
ans=calc(lx,ly);
ansx=lx,ansy=ly;
while(double(clock())/CLOCKS_PER_SEC<0.96) SA();
printf("%.3lf %.3lf",ansx,ansy);
return 0;
}
上面介绍的几种算法其实是可以互相融合的。
来看一下这道题:
P2503 [HAOI2006]均分数据 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
[HAOI2006]均分数据
题目描述
已知 \(n\) 个正整数 \(a_1,a_2 ... a_n\) 。今要将它们分成 \(m\) 组,使得各组数据的数值和最平均,即各组数字之和的均方差最小。均方差公式如下:
其中 \(\sigma\) 为均方差,\(\bar{x}\) 为各组数据和的平均值,\(x_i\) 为第 \(i\) 组数据的数值和。
输入格式
第一行是两个整数,表示 \(n,m\) 的值( \(n\) 是整数个数,\(m\) 是要分成的组数)
第二行有 \(n\) 个整数,表示 \(a_1,a_2 ... a_n\)。整数的范围是 \([1,50]\)。
(同一行的整数间用空格分开)
输出格式
输出一行一个实数,表示最小均方差的值(保留小数点后两位数字)。
样例 #1
样例输入 #1
6 3
1 2 3 4 5 6
样例输出 #1
0.00
提示
样例解释:\(1,6\)、\(2,5\)、\(3,4\) 分别为一组
【数据规模】
对于 \(40\%\) 的数据,保证有 \(m \le n \le 10\),\(2 \le m \le 6\)
对于 \(100\%\) 的数据,保证有 \(m \le n \le 20\),\(2 \le m \le 6\)
因为数据范围很小,所以这道题模拟退火和随机排序都能过。
不难想到,真正会影响最终结果的只有每组数的平均值,每一组的平均值越小,结果越优。
于是,我们可以在随机的过程中采用一种贪心的策略来提高正确率
即:每次都把当前的这个数分到平均值较小的那一组里面
对正常的算法这种贪心显然是错误的,但随机化算法不管这些。
随机排序代码:
#include<bits/stdc++.h>
using namespace std;
inline int read() {
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
return f?-x:x;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+48);
}
int n,m,x,y;
double a[102],sum,ans=9999999.999,num[102];
double Calc() { //求值函数
memset(num,0,sizeof(num));
int t=1;
for (int i=1;i<=n;++i) {
t=1;
for(int j=1;j<=m;++j) {
if (num[j]<num[t]) t=j; //采用贪心策略提高正确率
}
num[t]+=a[i];
}
double ANS=0;
for (int i=1;i<=m;++i) {
ANS+=(num[i]-sum)*(num[i]-sum);
}
ANS/=m;
return sqrt(ANS);
}
void S_sort(){ //随机排序
for (int i=1;i<=400;++i) {
x=rand()%n+1; y=rand()%n+1;
while (x==y) y=rand()%n+1;
swap(a[x],a[y]);
double ANS=Calc();
ans=min(ANS,ans);
}
}
signed main(){
n=read(); m=read();
for (int i=1;i<=n;++i) {
x=read();
a[i]=double(x);
sum+=a[i];
}
sum/=m;
while(double(clock())/CLOCKS_PER_SEC<0.96){
S_sort();
}
printf("%.2lf",ans);
return 0;
}
模拟退火代码:
//注:该代码参数并没有调好
#include<bits/stdc++.h>
using namespace std;
inline int read() {
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
return f?-x:x;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+48);
}
double T,ep=0.97;
int n,m,x,y;
double a[102],sum,ans=9999999.999,num[102],AS=9999999.99;
double Calc() { // 求值函数
memset(num,0,sizeof(num));
int t=1;
for (int i=1;i<=n;++i) {
t=1;
for(int j=1;j<=m;++j) {
if (num[j]<num[t]) t=j;
}
num[t]+=a[i];
}
double ANS=0;
for (int i=1;i<=m;++i) {
ANS+=(num[i]-sum)*(num[i]-sum);
}
ANS/=m;
return sqrt(ANS);
}
void SA(){ //模拟退火
T=100000; //设置初始温度
while (T>1e-14) {
x=rand()%n+1; y=rand()%n+1;
while (x==y) y=rand()%n+1;
swap(a[x],a[y]);
double ANS=Calc();
if (ANS<ans) ans=ANS,AS=ANS;
else {
if ((ANS-ans)/T<(double)rand()/RAND_MAX) ans=ANS;
//当得到的解不是目前最优解时,根据温度大小,有一定概率接受该解
}
T*=ep;//降温
}
}
signed main(){
srand(2023);
n=read(); m=read();
for (int i=1;i<=n;++i) {
x=read();
a[i]=double(x);
sum+=a[i];
}
sum/=m;
while(double(clock())/CLOCKS_PER_SEC<0.96){
SA();
}
printf("%.2lf",min(ans,AS));
return 0;
}
可以看到,模拟退火和随机排序的求值函数是一样的。这道题目里,求值函数都用了随机排序。
各类随机化算法的求值函数基本是一直的,唯一不同只不过是在接受答案时有所区别
模拟退火实质上就是在接受答案的时候有一定概率接受非当前最优解,从而跳出局部最优解。计算函数与其余随机化算法大同小异。有时几种随机化算法可以杂糅使用,毕竟随机化算法做题基本都是乱搞,多少是要沾点玄学的,没必要纠结太多。
除上述算法外,随机化算法还有蚁群算法和遗传算法等,但奈于博主水平有限,本篇博客就到这里了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号