2017 ACM ICPC Asia Regional - Daejeon Programming Contest
XJTU ICPC Team Selection - Summer 2021 - Day1
A. Broadcast Stations
0.5 seconds
Description
给定一个树,\(n\)个点,点\(i\)可以覆盖与其距离小于等于\(p(i)\)的点。要使所有点都被覆盖,\(\sum p(i)\)最小是多少
\(1\leq n\leq 5000\)
Solution
树形dp
B. Connect3
0.5 seconds
Description
4*4的棋盘,黑白双方轮流下。只有在一个格子下方的格子有棋子时,该格才能放棋子(第一行的格子除外)。当横着、竖着或斜着有3个子连成线时胜利。已知第一步黑棋下第一行第\(x\)列,最后一步白棋下第\(a\)行第\(b\)列。求最后棋盘有多少种可能的状态(不考虑落子的顺序)
Solution
由于最多16步,每步最多4种下法。直接枚举,\(4^{16}\approx 4e9\),然后判断是否合法,记录所有合法的状态(不到\(3^{16}\)),去重。
不过\(4^{16}\)是过不了的,由于\(x,a,b\)都小于等于4,所以打表即可。
C. Game Map
1 second
Description
给定一个无向连通图,可以从结点\(a\)走到结点\(b\)当且仅当\(a,b\)相邻且与\(b\)相邻的点的个数大于与\(a\)相邻的点的个数。任选一个点作为起点。问做多经过几个点。
\(1\leq n\leq 100000,n-1\leq m\leq 300000\)
Solution
按题意可以建一个DAG,在DAG上跑dp求出最长路即可
D. Happy Number
0.2 seconds
Description
定义\(f(n)=n\)的各位的平方和(十进制)。给定\(n\),判断一直让\(n=f(n)\)会不会使得\(n\)最终变为\(1\)。
\(1\leq n\leq 10^9\)
Solution
按题意模拟即可,遇到循环节停止。由于范围内任何数取\(x=f(x)\)后都一定在\(729\)以内,所以循环节长度最大为\(729\)。
E. How Many to Be Happy?
0.5 seconds
Description
给定一个简单无向连通图。对于边\(e\),定义\(H(e)\)为最少删掉几条边可以使\(e\)在最小生成树中。求\(\sum H(e)\)
\(n\leq 100,m\leq 500\)
Solution
枚举每条边。考虑这样建图:点集和原图相同,原图中每条边权小于该边的边,建一条容量为1的边。这条边的\(H\)值就是新图的最小割。由最大流最小割定理,跑最大流即可。虽然dinic算法复杂度\(O(n^2m)\),这样总复杂度\((n^2m^2)\)过不了,但所有边容量都为1时dinic算法复杂度\(O(min(n^{0.67}m,m^{1.5})\)这样就能过了。
F. Philosopher’s Walk
0.5 seconds
Description
Philosopher在一个一个n*n的网格中按如图所示的路线(皮亚诺曲线/希尔伯特曲线)从左下(1,1)走到右下(n,1)。求他走的第\(m\)个格子的坐标。
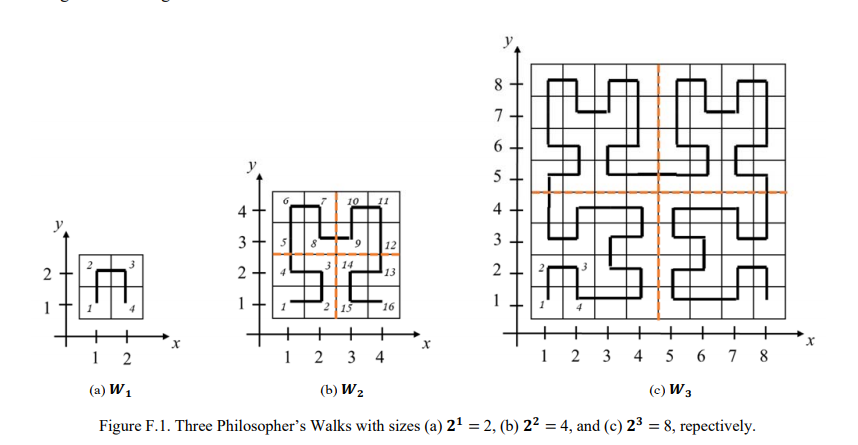
\(n=2^k,m\leq n^2,0<k\leq 15\)
Solution
设\(f(n,m)\)为要求的坐标,由于其自相似性,\(f(n,m)\)可由\(f(\frac{n}{2},m\bmod\frac{n^2}{4})\)得到。递归求解即可
G. Rectilinear Regions
0.5 seconds
Description
Solution
H. Rock Paper Scissors
1 second
Description
一个石头剪刀布机器,它的行动由一个由R(石头)、S(剪刀)、P(布)构成的字符串(长为\(n\),\(n\leq 100000\))表示。
你的行动也由一个串(长为\(m\),\(m<n\))表示。
你可以选定对方串的一个长为\(m\)的子串,与你的串相比,你每赢一局就得1分。求最大得分
Solution
据说是多项式
I. Slot Machines
2 seconds
Description
Solution
J. Strongly Matchable
3 seconds
Description
匹配:图中没有任何两条边拥有一个共同顶点的子图
完美匹配:覆盖图的所有点的匹配
Strongly Matchable:将图中的点平分为两部分,删去两端都在同一部分的边,若对于所有的平分方式,新图都有完美匹配,则称其Strongly Matchable。
给定一个图判断它是否Strongly Matchable。
Solution
K. Untangling Chain
0.5 seconds
Description
给定一条由\(n\)个“前进x步,左转”或“前进x步,右转”组成的路径。你可以改变每次前进的步数,但不能改变转向。请构造一条路径使得它不与自身相交且每次前进的步数\(\in [1,n]\cap N\)
\(1\leq n\leq 10000\)
Solution
先对转向信息进行前缀和,得到每次走的方向。对于向上的边记录他前面最近一条向下的边,对于向左的边记录他前面最近一条向右的边,对于向下的边记录他前面最近一条向上的边,对于向右的边记录他前面最近一条向左的边。每条边初始边长设为1,从后向前枚举,若该边边长为\(a\),则其记录的边边长\(+=a\)



