数模竞赛-长三角旅游路线

 题目 旅游路线规划问题
题目 旅游路线规划问题
摘 要:
本文针对在一个城市之间距离相对较近的城市群中规划旅行线路的目标规划问题,运用建立数学模型的方法,在MATLAB软件的协助下,解决了不同限制条件下的路线规划问题,具体如下:
首先,为解决该问题,我们查询了大量的数据:为每个城市进行打分,并按照分数从大到小的顺序,选择了10个城市作为目标城市;然后根据每个城市所有的景点进行合理的人工筛选,最终选定20个目标景点,并为每个景点进行打分;最后确定了游玩各个景点所需要的消费。
针对问题一,我们首先认定在旅行时间的限制下获得最高景点分数和为目标进行模型的建立,其次通过贪心算法先求出一个限制条件范围内的满意解,然后通过蚁群算法以及迭代循环的方式求出限制条件下的最优解,最后通过比较两种算法的结果,发现贪心算法虽然可以求出限制条件范围内的局部最优解,但不是全局最优,最终我们以蚁群算法所得到的解作为问题一的最优解;
针对问题二,我们首先分析了题目的要求,发现了问题二与问题一的相似性,其次对问题一的模型做了修改,从而确定了问题二的模型,在不考虑住宿费的条件下求得当前所有的可行解,然后根据所求得的可行解分别计算他们所需要的旅行消费及旅行时间,最后根据住宿费(只与旅行天数有关)的限制条件进行可行解范围的缩小,比较剩余可行解对应的旅行路线所获得的分数,选取分数最高的可行解作为问题二的解;
针对问题三,我们首先根据旅行时间的限制和旅行费用的限制在前两问的模型基础上做了修改,建立了问题三的模型,其次在求解模型的过程中,通过归一加权的方式,对时间限制和费用限制两个约束条件进行合成,求解出满足该合成约束条件的所有可行解,然后通过可行解同时代入时间约束和费用约束的方式进一步缩小可行解的规模,最后通过计算剩余可行解对应的规划路线能够获得的分数,选择分数最高的路线作为我们的结果;
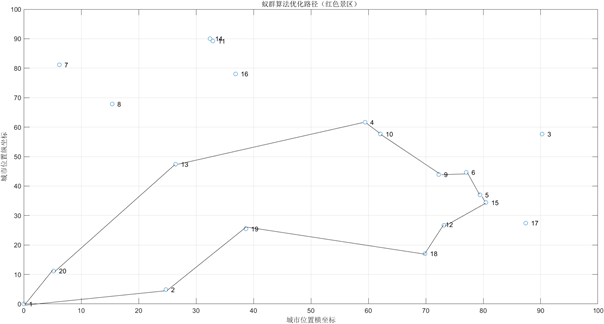
针对问题四,我们首先经过分析确定沿用问题三的模型,然后对数据预处理中的景点分数进行更新,将红色景点的权重加入景点分数的计算过程,最后,运用问题三的求解方式,对问题四进行求解;
针对问题五,我们首先通过数据查询对激励计划值进行了计算,然后在原有2-4问的基础上,对旅行费用上限进行了每日更新,最后经过求解的结果进行合理假设,假定小李的旅游规划中,只有我们预先确定的20个景点,在旅行费用足够的情况下,我们认定在获得所有景点的分数后,小李的旅行规划是最完美的,即求得了我们所需要的最优解。
关键词:蚁群算法 贪心算法 多目标规划
目录
附录
正文题目
一、问题重述
值此毕业季来临之际,来自浙江杭州的大学生小李同学准备给自己安排一个毕业旅行,同时帮助"长三角旅游推广联盟"考察一下长三角地区旅游资源的开发和利用情况。小李同学家境良好,在做旅行计划时,他希望这是一个有美食、有风景、令人难忘的毕业旅行。
搜集相关数据,建立数学模型,帮助小李同学规划旅行计划,讨论并解决以下问题:
问题一:
若小李同学只有两个星期的旅行时间,试为他规划旅行计划。
问题二:
若小李同学时间比较充裕,但能够支配的旅行资金只有5000元钱,试为他规划旅行计划。
问题三:
若小李同学只有两个星期的旅行时间,也只有5000元钱作为旅行资金,试为他规划旅行计划。
问题四:
小李的爷爷是个退伍军人,目前已经退休在家,时常怀念曾经的峥嵘岁月,准备来杭州与小李共同出游,试为他们规划不超过两个星期、两人旅行总费用不超过1万元的旅行计划。
问题五:
小李还是一个兼职新媒体人,bilibili平台粉丝数达52.5万。在旅行中,他想通过B站更新,在涨粉的同时为旅行经费添砖加瓦。小李的B站收入仅限于"播放量+点赞数+投币+收藏"所带来的流量变现,且该收益与当天的具体旅游景点密切相关。假设在其旅行时间内更新频率为日更,更新内容为当天旅行的1小时vlog,报酬按日结算,结算的费用可以补充为旅行费用,试查找相关数据,重新完成2-4问。
二、基本假设与符号说明
2.1基本假设
1.城市之间交通均采用高铁;
2.城市之内景点之间交通均采用公共交通;
3.出游天气均为适合游玩的天气;
4.保障出行期间的充足睡眠,但入睡时间不确定,可自由分配;
5.旅行途中无意外,行程无延误;
6.所有景点门票费用均以普通成年人票为准;
7.不考虑景区开放时间对行程安排的影响;
8.假设旅游在限制条件内旅行终点为杭州;
9.假设旅行过程中的住宿费用只与旅行天数有关,每旅行一天,住宿费为150元;
10.本文所涉及到的时间变量均以小时计;
11.假设一天24小时之内的游玩时间为12小时。
2.2符号说明
|
|
表示通过计算之后得出的各城市的分数; |
|
|
表示通过计算之后得出的各景点的分数; |
|
|
表示旅行规划中的起始地点的标号; |
|
|
表示旅行规划中的目的地点的标号; |
|
|
表示第j个目标景点的逗留时间; |
|
|
表示第i个景点到第j个景点的路程花费的时间; |
|
|
表示到达第j个景点的序列号; |
|
|
0-1决策变量,表示是否选择第i个地点到第j个地点之间的路线,若选择则为1,否则为0; |
|
|
表示第i个景点到第j个景点的路程费用; |
|
|
表示第j个景点的景区内消费; |
|
|
表示旅行路线的总消费 |
|
|
表示旅行路线所花费的总时间 |
三、问题分析
问题一:对于题干,首先提到了旅游范围为长三角城市群,所以选择的景点需要在范围内。同时,要求是一个有美食有风景的旅游,所以,对于景点的搜索,为了缩小范围,选用先选城市后选景区的策略。对于城市选择,我们采用了对于城市的美食和风景进行加权得到城市分数,这个分数可以反映这个到达这个城市的满意度。将分数进行排名后选择分数最高的十个城市来选择景点。同时在这些城市里进行景点选择。最终选择出20个景点作为旅行中的节点。并且根据实际情况设置在该节点的滞留时间和花费。将实际问题转化为类似TSP模型的数学模型进行求解。通过将时间设置为约束条件,每个节点最多经过一次的情况下,目标达到景区分数最大。
问题二:对于问题二,题中对旅行者的时间不再进行限制,但是对于旅行经费进行了限制。对于旅行经费的花销,主要分成三个部分,交通费用,住宿费用和景区消费。对于交通费用以部分实际数据和直线距离进行拟合,得到拟合程度好的函数,确定交通费用和时间。
同时,对于景区消费进行了基于该城市人均消费的估计。建立基于出费用一定的情况下分数最高的旅游路线规划模型。
问题三:问题三是有多个限制条件的不确定经过点的TSP问题。对于这个问题,首先需要确定单个限制条件的成立,将可行解进行第二个限制条件的约束运算,获得一部分可行解。对于可行解进行目标函数的运算,最后算出满意解。
问题四:在问题四中,小李和爷爷一起旅游,单人的旅行费用和旅行时间和问题三相同。但不同之处在于小李的爷爷作为退休军人想要去游览红色景点,因此,依据旅行者的偏好,我们对于所有具有红色景点属性的景点的分数进行了一定的加成,使城市分数(满意度)提高,使最后的路线安排尽可能的出现更多的红色景点,但最终的决策变量还是获得的城市分数。
问题五:问题五引入了一种新的机制,叫创作激励,也就是说在旅行过程中可以获得收益来补充旅行费用。根据网络搜集的信息知,激励计划获得的钱数与视频播放量,点赞,收藏,投币都有一定关系。在网络上寻找粉丝数量相近,最近一天有过新视频发布的几位UP。通过统计他们的数据可以大约求得小李的视频平均收益。又视频的播放数据和这天的旅行景点密切相关,当旅行的景点评分越高时,可以得到更多的收益。并将此变量引入2-4的模型计算,求出满意的解。
四、模型的建立与求解
4.1数据预处理
4.1.1城市选择
为了在保证旅游体验感的同时兼顾考察长三角地区旅游资源的开发和利用情况这个任务,我们在进行旅游规划的时候对长三角城市群中的26个城市进行了打分,分数越高代表旅行体验感越好。在附件1中我们通过城市风景指数(由各地知名景区按权相加得出)、城市美食指数(由百度搜索频次给出)以及风景与美食所对应的权重(由大众旅游目的的偏好得出)对城市分数进行计算:
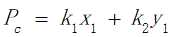
其中:
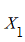 表示城市对应的美食指数;
表示城市对应的美食指数;
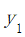 表示城市对应的风景指数;
表示城市对应的风景指数;
 表示美食所对应的权重;
表示美食所对应的权重;
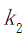 表示风景所对应的权重;
表示风景所对应的权重;
通过数据预处理,我们根据城市分数的排名选择了10个城市作为备选城市。
4.1.2景点选择
考虑到题目中所给的条件,在备选城市中,我们以风景、美食兼备和景点种类多样化的原则,在城市中每20个景点挑选一个景点,最终确定了附件2中给出的20个景点。我们根据携程旅游APP中用户对景点的评分、景点所在城市的美食指数以及风景与美食所对应的权重(由大众旅游目的的偏好得出)为备选景点中的每个景点进行打分,分数越高代表旅行体验感越好。
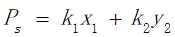
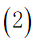
其中:
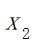 表示景点所在城市对应的美食指数;
表示景点所在城市对应的美食指数;
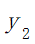 表示景点的评分;
表示景点的评分;
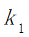 表示景点所在城市的美食所对应的权重;
表示景点所在城市的美食所对应的权重;
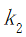 表示景点所在城市风景所对应的权重;
表示景点所在城市风景所对应的权重;
4.1.3景区内消费计算
景区消费我们通过景区所在城市的人均时消费赋权值后与景区门票相加求得,结果见附件3。
4.2问题一模型的建立与求解
4.2.1模型的建立
考虑到问题一限制旅行时间控制在两周之内,但同时又要兼顾旅行体验和帮助"长三角旅游推广联盟"考察长三角地区旅游资源的开发和利用情况的任务。我们在建立模型的过程中抽象出爽度这一概念,用来表示旅行体验感,并规定爽度越高,则旅行体验感越好、考察任务完成情况越好。
目标函数:
我们用所经过的景点分数总和来表示爽度。该问题类似于TSP问题,所以我们在TSP问题的模型的基础上加以修改,进行模型的建立。本模型以旅行过程中在限制时间内获得最高爽度为目标:
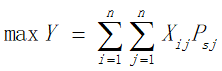
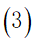
约束条件:
a.为兼顾旅行过程中的考察任务,应该尽量多的经过不同的景点,所以我们规定每个景点的分数不可重复获得,将每个景点看作图中的一个顶点,即每个顶点至多有一条边进去、至多有一条边出来,同时有边进去就必须有边出来:
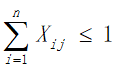
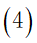
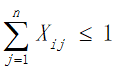
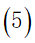
b.由于旅行时间限定为2周,所以在获得最大爽度的同时我们需要将旅行时间约束在2周之内,即所有目的地点的逗留时间与景点之间的路程所花费的时间之和加上返杭的时间不超过168小时:
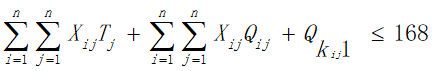
综上所述,问题一的模型为:
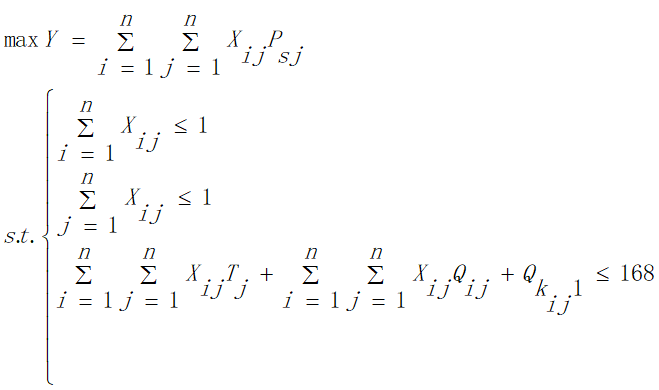
4.2.2模型的求解
在模型一的求解中,我们需要在旅行时间的限制下求出爽度最高值。
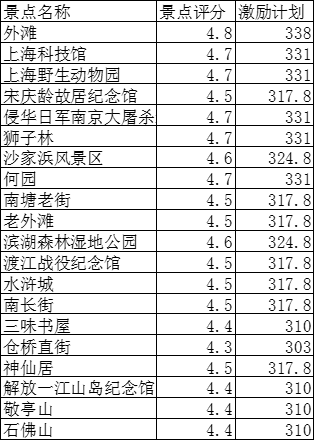
在求解的过程中,为方便解的表示,我们对景点进行了编号,具体如下:
表1 景点编号
|
景点标号 |
景点名称 |
|
1 |
外滩 |
|
2 |
上海科技馆 |
|
3 |
上海野生动物园 |
|
4 |
宋庆龄故居纪念馆 |
|
5 |
侵华日军南京大屠杀遇难同胞纪念馆 |
|
6 |
狮子林 |
|
7 |
沙家浜风景区 |
|
8 |
何园 |
|
9 |
南塘老街 |
|
10 |
老外滩 |
|
11 |
滨湖森林湿地公园 |
|
12 |
渡江战役纪念馆 |
|
13 |
水浒城 |
|
14 |
南长街 |
|
15 |
三味书屋 |
|
16 |
仓桥直街 |
|
17 |
神仙居 |
|
18 |
解放一江山岛纪念馆 |
|
19 |
敬亭山 |
|
20 |
石佛山 |
|
0 |
杭州东 |
方法一(基于贪心算法的问题一模型求解):
贪心算法的基本思想是,根据所要求的问题寻找一个贪心点,首先根据这个贪心点对事物进行排序,然后根据限制条件进行线型扫描直到条件不满足。
针对本问题,我们在MATLAB软件中编写程序进行求解,具体代码文件见附录1。首先根据中给出的景点分数从高到低对景区进行排序并为其编号(A,B,C,…),不考虑排序后的景点的逗留时间的长短,在考虑最后一个景点返回杭州的时间的情况下,按照线型扫描的方式累加每个景点的逗留时间,直至时间限制,得出最终的旅行路线,此种方法所求得的结果为:
景点游玩顺序:
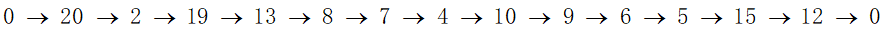
以此顺序进行游玩,
得到的总分数:753.26
最少需要的时间:153.2094
方法二(基于蚁群算法的问题一模型求解):
蚁群算法是属于一种求解组合最优化问题的新型通用启发式方法,该方法具有正反馈、分布式计算和富于建设性的贪婪启发式搜索的特点。蚁群算法是一种以生物学为基础的仿生优化算法,全局寻优能力强。用蚂蚁的行走路径表示待优化问题的可行解,整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多,随着时间的推进,较短的路径上累积的信息素浓度逐渐增高,选择该路径的蚂蚁个数也愈来愈多。最终,整个蚂蚁会在正反馈的作用下集中到最佳的路径上,此时对应的便是待优化问题的最优解。首先,我们要引入蚂蚁的概念。蚂蚁具有记忆功能,并具有以下特征:
1) 根据信息素浓度和启发式信息,用相应的转移概率选择下一个城市。
2) 将已经走过的城市放入记忆表中,记忆表里的城市将不再被选择为下一个城市。
3) 完成一次循环后,根据整个路径的长度来释放相应的信息素,并更新走过的路径上的信息素。
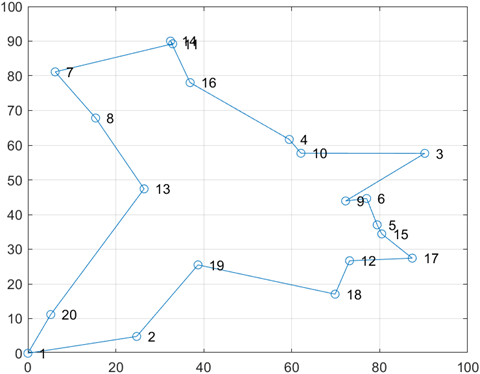
第一步:确定景点坐标
根据附件3中所给出的景点之间的距离,在MATLAB软件中编写程序(具体代码文件见附录2)确定景点坐标,得出景点的坐标图:
图1 景点坐标
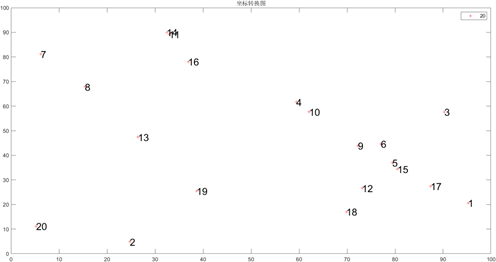
第二步:确定旅行路线
在不考虑时间限制的情况下,以时间最短为目标,相当于求解最短路径问题,利用蚁群算法求出我们所确定的20个景点的最优旅行路线如下:
图2 最短时间路线图

第三步:求出可行解
以下分为现有最优旅行路线的旅行时间超过时间限制和不超过时间限制两种情况:
①时间未超出限制:
在时间未超出限制的情况下,当前旅行路线即为所求最优解,经过预分析得到此种情况不是我们的最优解,所以排除。
②时间超出限制:
利用迭代循环的方式,在当前旅行路线中依次选择n(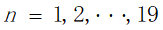 )个景点进行淘汰,直至路线上所有景点逗留时间的总和控制在限制时间之内,最后分别计算出淘汰之后的路线所花费的时间以及所获得的爽度,将此过程获得的可行解代入下一步进行求解。
)个景点进行淘汰,直至路线上所有景点逗留时间的总和控制在限制时间之内,最后分别计算出淘汰之后的路线所花费的时间以及所获得的爽度,将此过程获得的可行解代入下一步进行求解。
第四步:求出最优解
在上一步得出的可行解的基础上进行爽度值的比较,选出爽度最高的解,即为我们所要求的最优解。
通过方法二所求得的最优解为:
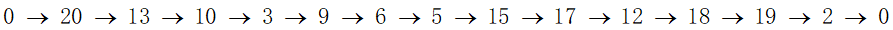 以此顺序游玩,
以此顺序游玩,
得到的总分数:990.19
最少需要的时间:160.29
4.2.3算法的比较
通过比较贪心算法和蚁群算法的结果,可以得出,贪心算法虽然可以求得局部最优的可行解,但是其结果并不是最优的,而蚁群算法是在时间利用率最高的情况下,获得了更高的分数。
4.3问题二模型的建立与求解
4.3.1模型的建立
问题二与问题一类似,同样选择对TSP问题模型修改进行本问题模型的建立。
①由于住宿费只与旅行天数有关,所以我们首先在不考虑住宿的情况下建立模型,求出旅行路线。
目标函数:
我们用所经过的景点分数总和来表示爽度。所以本模型以旅行过程中在限制时间内获得最高爽度为目标:
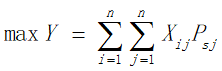
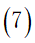
约束条件:
a.为兼顾旅行过程中的考察任务,应该尽量多的经过不同的景点,所以我们规定每个景点的分数不可重复获得,将每个景点看作图中的一个顶点,即每个顶点至多有一条边进去、至多有一条边出来,同时有边进去就必须有边出来:
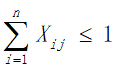
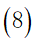
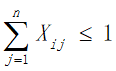
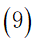
b.由基本假设得出住宿费的范围大致为 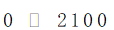 ,由于旅行经费限定为5000元,即所有目的地点的景区内消费与景点之间的路程花费之和加上返杭的路程费以及旅行过程中的住宿费用不超过5000元,所以在获得最大爽度的同时我们需要将住宿费之外得旅行花费约束在元以内:
,由于旅行经费限定为5000元,即所有目的地点的景区内消费与景点之间的路程花费之和加上返杭的路程费以及旅行过程中的住宿费用不超过5000元,所以在获得最大爽度的同时我们需要将住宿费之外得旅行花费约束在元以内:
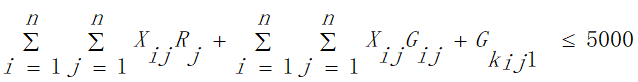
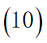
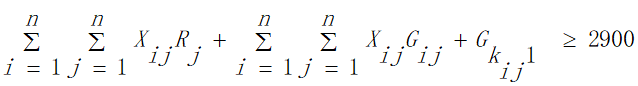
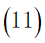
综上所述,问题二的模型为:
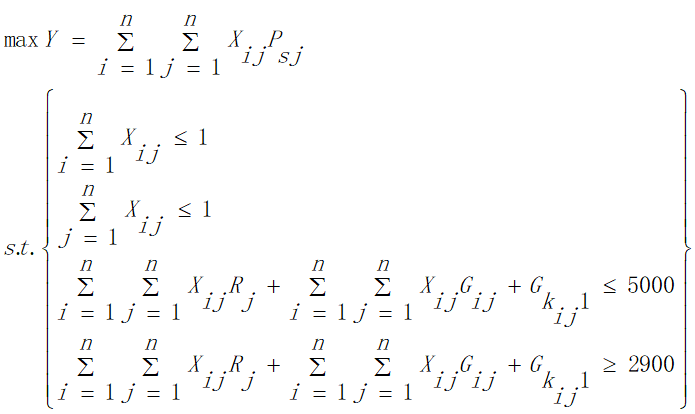
②根据第一步建立的模型所求出的所有可行的旅行路线,计算出当前路线的总消费:
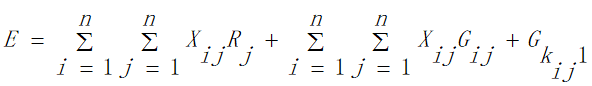
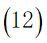
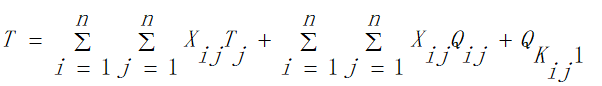
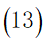
③在住宿费的约束下,选择所有可行解中的最优解作为我们模型的计算结果:
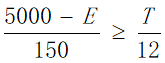
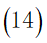
4.3.2模型的求解
①问题二的模型基本上与问题一模型相似,我们同样采用蚁群算法进行模型的求解,首先在去除住宿费的情况下,求出旅行路线的所有可行解;
②我们根据所求得的所有可行路线,分别计算出它们所需要的金钱花费E以及时间总和T,在此我们通过MATLAB软件对路程消费进行计算界定,方法如下:
(代码中x表示消费,y表示距离)

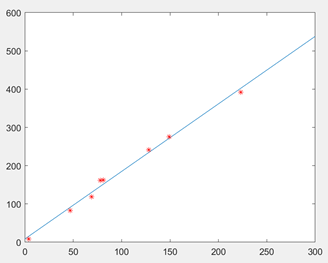
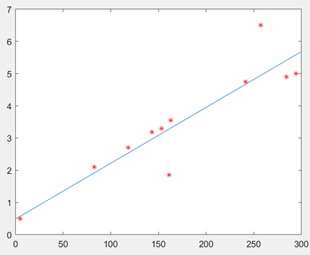
由MATLAB软件所呈现出来的线性关系为: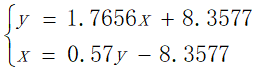
图3 交通的消费、距离拟合图像
(代码中y表示时间,x表示距离)

由MATLAB软件所呈现出来的线性关系为: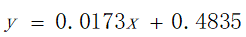
图4 交通的时间、距离拟合图像
③在以上模型所求得的可行解中,我们根据公式(14)进行注意筛选,最后从剩余可行解中寻找景点分数和最大的解作为最优解的旅行路线如下:
图5 问题二解路线
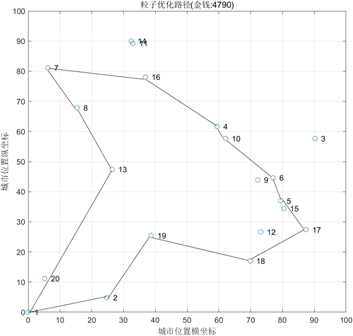
旅行路线为:
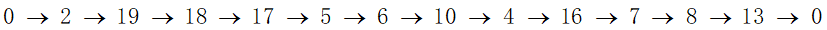 得到的总分数:812.22
得到的总分数:812.22
旅行消费为:4790元
4.4问题三模型的建立与求解
4.4.1模型的建立
问题三中要求我们在旅行费用限制和时间限制的条件下,为小李规划旅行路线,沿用前两问所提出的爽度的概念,我们需要在满足限制条件的同时,获得尽量高的分数。
目标函数:
我们以经过的所有景点所获得的总分作为目标函数:
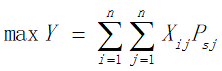
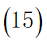
约束条件:
a.为兼顾旅行过程中的考察任务,应该尽量多的经过不同的景点,所以我们规定每个景点的分数不可重复获得,将每个景点看作图中的一个顶点,即每个顶点至多有一条边进去、至多有一条边出来,同时有边进去就必须有边出来:
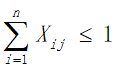

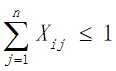
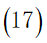
b.由于旅行时间限定为2周,所以在获得最大爽度的同时我们需要将旅行时间约束在2周之内,即所有目的地点的逗留时间与景点之间的路程所花费的时间之和加上返杭的时间不超过168小时:
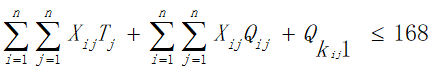
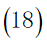
c.由于旅行经费限定为5000元,所以在获得最大爽度的同时我们需要将旅行花费约束在5000元以内,即所有目的地点的景区内消费与景点之间的路程花费之和加上返杭的路程费以及旅行过程中的住宿费用不超过5000元:
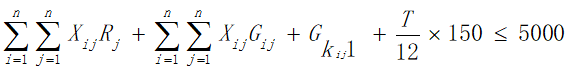

综上所述,问题三的模型为:
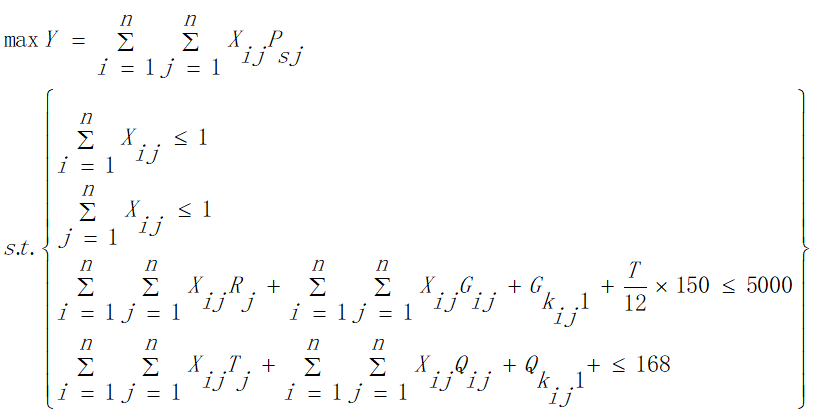
4.4.2模型的求解
①通过归一加权的方式,对时间限制和费用限制两个约束条件进行合成,求解出满足该合成约束条件的所有可行解;
②可行解同时代入时间约束和费用约束,进一步缩小可行解的规模;
③计算剩余可行解对应的规划路线能够获得的分数,通过比较,选择分数最高的路线作为我们的结果;
通过MATLAB进行求解,最终的结果为:
图6 问题三解路线
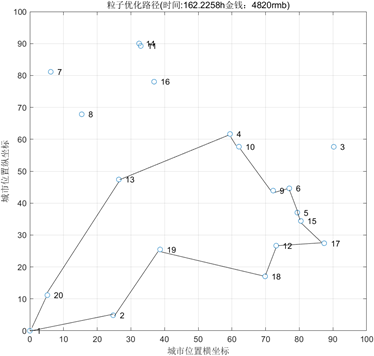
旅行路线为:
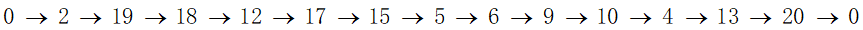 得到的景点分数和为:957.52
得到的景点分数和为:957.52
旅行时间为:162.2258
旅行消耗为:4820
4.5问题四模型的建立与求解
4.5.1模型的建立
经过分析,我们将问题三的模型沿用至问题四,由于预设条件中假设所有门票均以普通成年人票价计算,所以我们在建立模型的过程中默认小李和爷爷将旅行费用10000元平分。此时,题目要求我们在旅行费用限制5000元和时间限制2周的条件下,规划一条旅行路线,沿用爽度的概念,我们需要在满足限制条件的同时,获得尽量高的分数。
目标函数:
我们以经过的所有景点所获得的总分作为目标函数:
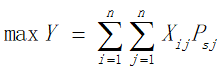
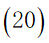
约束条件:
a.为兼顾旅行过程中的考察任务,应该尽量多的经过不同的景点,所以我们规定每个景点的分数不可重复获得,将每个景点看作图中的一个顶点,即每个顶点至多有一条边进去、至多有一条边出来,同时有边进去就必须有边出来:
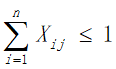
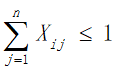
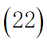
b.由于旅行时间限定为2周,所以在获得最大爽度的同时我们需要将旅行时间约束在2周之内,即所有目的地点的逗留时间与景点之间的路程所花费的时间之和加上返杭的时间不超过168小时:
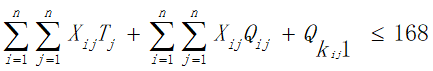
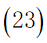
c.由于旅行经费限定为5000元,所以在获得最大爽度的同时我们需要将旅行花费约束在5000元以内,即所有目的地点的景区内消费与景点之间的路程花费之和加上返杭的路程费以及旅行过程中的住宿费用不超过5000元:
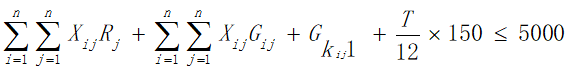
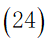
综上所述,问题三的模型为:
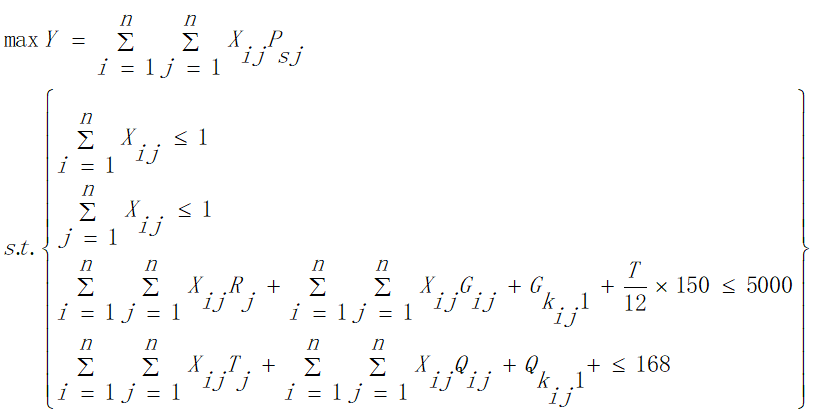
4.5.2模型的求解
①对数据预处理中的景点分数进行更新,将红色景点的权重加入景点分数的计算过程,最后,运用问题三的求解方式,对问题四进行求解
通过MATLAB进行求解,最终的结果为:
图7 问题四解路线
旅行路线为:
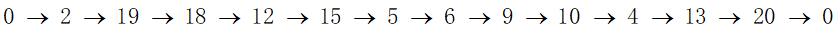 得到的景点分数和为:987.55
得到的景点分数和为:987.55
旅行时间为:167.59
4.6问题五模型的建立与求解
4.6.1模型的建立
①对于问题二,由于没有时间的限制,我们只需要根据问题二原有的模型,求出最小消费下的最优路径,所以本问求解的过程沿用问题二中的模型;
②对于问题三,我们通过MATLAB模拟问题二的模型可以得出走完所有的景点所花费的费用是在旅行资金(旅行预算+每日收益)之内的,所以我们不需要考虑消费限制,即问题转化为沿用问题一的模型,求解在2周时间限制内的最优路径;
③对于问题四,考虑到小李与爷爷共同出行,此时b站收益平均到两个人的花费中,相当于原问题三的求解,即在时间限制和消费限制的情况下求出最优解,那么此题的模型即为在问题三的模型的基础上,将b站收益的1/2加入到消费限制的约束条件中;
4.6.2模型的求解
①激励计划的每日收益计算。
根据网络信息可知,激励计划的收益与播放量,点赞数,收藏量和硬币数有关。其中,对于某一个视频而言,点赞数和播放量的比值决定播放量的千分收益。10%点赞率千分播放收益为3元,5%点赞率千分播放收益为2.3元,3%点赞率千分播放收益为2元。收藏和投币按十倍转化为播放量。由2021.5.22—2021.5.23的50W左右粉丝数UP主新发布视频的数据统计(如下表所示)取平均值,作为小李的视频的平均数据。
表2 50W粉丝的UP视频数据
|
up主标号 |
粉丝数/w |
播放量 |
点赞 |
投币 |
收藏 |
点赞率% |
|
1 |
41.5 |
72000 |
8671 |
338 |
341 |
12 |
|
2 |
49.7 |
32000 |
1643 |
230 |
171 |
5 |
|
3 |
49.6 |
113000 |
10000 |
5970 |
1276 |
8 |
|
4 |
49.7 |
158000 |
17000 |
5950 |
1620 |
10.7 |
|
5 |
49.3 |
137000 |
9732 |
1408 |
582 |
7.1 |
|
和 |
239.8 |
512000 |
47046 |
13896 |
3990 |
|
|
平均 |
47.96 |
102400 |
9409.2 |
2779.2 |
798 |
9.1 |
最终平均收益J=2.3*(播放量+10*(收藏+投币))/1000=306.3
而不同景点的视频收益,取决于该景点评分。而平均评分的景点,视频收益为平均收益。据此得到各景点的激励计划收益。如下表所示。
表3 各景点的激励计划视频收益
②问题二在MATLAB中所得到的路线图为:
图8 问题五中问题二的重新求解路线图
旅行路线:
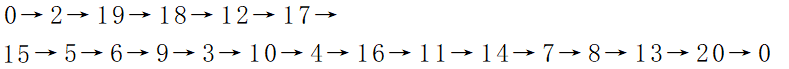
B站总收入:6410.2元
旅行总消费:5138.6
旅行所得景点分数:1257.71(全部的分数)
余额:1271.6
③经过分析,问题三的求解我们只需要考虑时间限制,所以采用问题一的计算方法进行求解,所得旅行路线为:
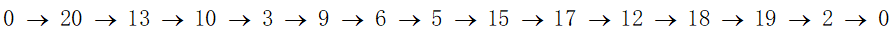
B站总收入:5241.6
旅行时间总和:160.29h
旅行总消费:4820
旅行所获得的景点总分数:990.19
④考虑到问题四中红色景点权值的提高对景点分数的影响,并在时间限制和消费限制的情况下求出最优解,通过MATLAB软件运行得出旅行路线为:
图9 问题五中问题四的重新求解路线图
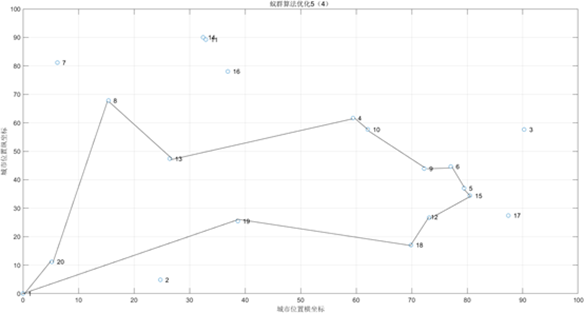
旅行路线为:
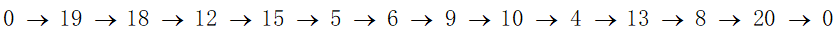
B站总收入:5543.5
旅行时间:166.54
旅行所得景点总分数:1025.11(因为红色景点权值被改变了)
旅行总消费:11543.1
五、模型总结
本文的模型建立与模型求解主要有以下几个优点:
1.采取了更为高效的蚁群算法,解决了路径规划的问题;
2.对于查询到的大量数据采取了加权求和的方法,将复杂的数据进行了简化,使模型求解过程中的数据代入更方便;
3.通过合理转化目标以及约束条件之间的关系,增强了模型的可移植性。
但是在理论与实际结合的过程中考虑的因素仍有不足,所以还存在以下几点不足:
1.模型建立的过程中缺乏对突发情况的考虑(旅行者的身体状况、出行天气状况等),导致模型对模型的应用广泛性不足;
2.对于城市评分及景点评分等数据的处理不够细化,可能导致数据的偏差引起结果的偏差;
3.由于数据量庞大,且题目没有给出,导致我们在模型的求解过程中没有强大的数据支撑,结果可能不够精确。
参考文献
[1] 崔之熠,王茂芝,刘国涛,等,蚂蚁算法在 TSP 问题求解的应用 [J],四川理工学院学报:自然科学版,24(3): 334-337,2011.
[2] 伍文城,肖建,基于蚁群算法的中国旅行商问题满意解[J],计算机与现代化,(8): 6-8,2002
[3] 方冬云.图论在旅游线路选择中的应用[J]. 长春工业大学学报(自然科学版). 2009(05)
[4] 曹文梁,康岚兰,基于遗传算法的混合蚁群算法及其在 TSP 中的应用研究[J],制造业自动化,33(2):91-93,2011.
[5]吴佩雯基于蚁群算法的点覆盖问题研究[J] 兰州交通大学学报 - 2019, 39(2
[6]肖桂霞,郑金华一种新的动态TSP模型及其求解方法[J], 计算机工程与应用 2008,44(3)
[7] 韦美艳湖南科技学院学报 基于多目标的TSP模型在物流配送中的应用[J] 湖南科技学院学报 2012 (8)
结语:这是第一次参加数模比赛,真滴是一点基础都没有,三个人就像愣头青一样,比赛的时候到处瞎撞,4天时间中有3天讨论+批斗弱小的我,真正开始动笔论文的时间只有最后那一天,而且回头看了看我的代码和建的模型,我代码有问题,模型也有一些小缺陷,想一想当时确实没有什么经验,就知道这是个熬夜的玩意,就在那瞎熬,熬了挺久的,但是感觉莫得卵用,最后一天关键时刻,我搁那睡觉,睡的是真滴爽hhhh,不过两个队友还是给力的,最终结果也不错,拿了一个省级二等奖(应该吧),校一等奖,也算是体验了一番。感动的我都要去吃饭了害
代码:Modeling/长三角竞赛-旅游 at master · instead-everyone/Modeling (github.com)

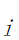
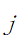

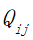
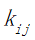
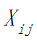
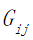
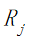
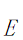

 浙公网安备 33010602011771号
浙公网安备 33010602011771号