5.感知机科普简介

• 本文由中山大学In+ Lab整理完成，转载注明出处!
• 团队介绍 传送门（http://www.cnblogs.com/inpluslab-dataplayer/p/8541380.html）

线性分类器起源

在实际应用中，我们往往遇到这样的问题：给定一些数据点，它们分别属于两个不同的类，现在要找到一个线性分类器把这些数据分成两类。


怎么分呢？把整个空间劈成两半呗（让我想到了盘古）。用二维空间举个例子，如上图所示，我们用一条直线把空间切割开来，直线左边的点属于类别-1（用三角表示），直线右边的点属于类别1（用方块表示）。
如果用数学语言呢，就是这样的：空间是由X1和X2组成的二维空间，直线的方程是X1+X2 = 1，用向量符号表示即为 \([1,1]^{T}[X1,X2]-1=0\) 。点x在直线左边的意思是指，当把x放入方程左边，计算结果小于0。同理，在右边就是把x放入方程左边，计算出的结果大于0。都是高中数学知识。
在二维空间中，用一条直线就把空间分割开了：


在三维空间中呢，需要用一个平面把空间切成两半，对应的方程是X1+X2+X3=1，也就是 \([1,1,1]^{T}[X1,X2,X3]-1=0\) 。


在高维（n>3）空间呢？就需要用到n-1维的超平面将空间切割开了。那么抽象的归纳下：如果用x表示数据点，用y表示类别（y取1或者-1，代表两个不同的类），一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面（hyper plane），把空间切割开，这个超平面的方程可以表示为(\(W^{T}\)中的T代表转置）：

$ W^T X+b=0 $

拓展到高维空间中（n>3）, 图像形式的可以不用想象，类推其代数表述形式即可。小结如下：
对于超平面S:

$ W^{T} X+b=0; $

对于点X(X是一个向量，表示多维空间内一点)，
若 $ W^{T} X+b>0 $ , 则点X在超平面S上面部分；
若 $ W^{T} X+b<0 $ , 则点X在超平面S下面部分；

感知机的学习策略

现在，我们在二维数据的情况下，一步步模拟感知机的大致的学习策略。


假设有若干点，分为两种类别，如图2所示，圈点和叉点分别表示两种不同的类别。为了确定一个合适的直线s使之能够将这两类点正确的区分出来，先随机选一条直线 $ S_0 $ 如下图2的形式：


我们看到，随机挑选的直线 $ S_{0} $ 并不能把所有的点都正确区分开来。由于在初始直线以上部分，叉点多于圈点，故令叉点为正类，圈点为负类。那么，图中标红的圈点和叉点就称为误分类点。那么将这些误分类点正确分类后，就能得到一条直线S能将所有的点正确分类。
接下来，开始模拟，直线 $ S_{0}:ax+by+c=0 $ 的变化过程。
先根据T1点，去调整参数a,b,c，更新直线S,如下图，得到更新后的直线$ S_{1} $ 。

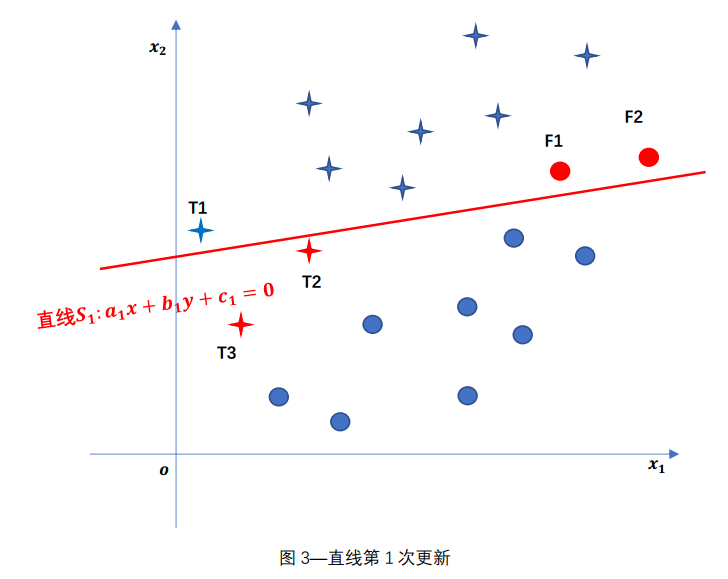
然后根据T2点，去调整参数a,b,c，更新直线S,如下图，得到更新后的直线 $ S_{2} $ 。


根据图中的误分类点，依次更新参数a,b,c，得到最终更新的直线S .

 

如图6所示，根据图中所有的误分类点，通过不断调整参数更新直线S，使得S能逐步将越来越多的点正确分类直至将所有的点都正确区分。最终得到的直线S就是感知机模型中所用到的形式。
于是最终的感知机模型：

$ f(x,y)=sign(a_{4} x+b_{4} y+c_4) $

小拓展

上述是在二维空间里的感知机模型，推广到n维空间中：

$ f(X)=sign(W∙X+b) $ $ W=(w_{1},w_{2},…,w_{n})，X=(x_{1},x_{2},…,x_{n}) $ , 其中，W称为系数向量，类比二维空间中的x,y的系数(a,b)。

直线具体的变化过程

上面举得栗子，只是讲述了感知机模型中的直线的变化流程，那么直线具体是怎么调整的呢，也就是说，关于直线的那些参数是怎么样一步步调整更新的呢？
为了便于感知机模型推广至高维空间，使用感知机模型的一般式进行演示。感知机模型：

$ f(X)=sign(W∙X+b) $ 在二维空间中， $ W=(w_{1},w_{2})，X=(x_{1},x_{2}) $ 。 还是以前面所举的那个小栗子来具体讲述直线的调整过程。

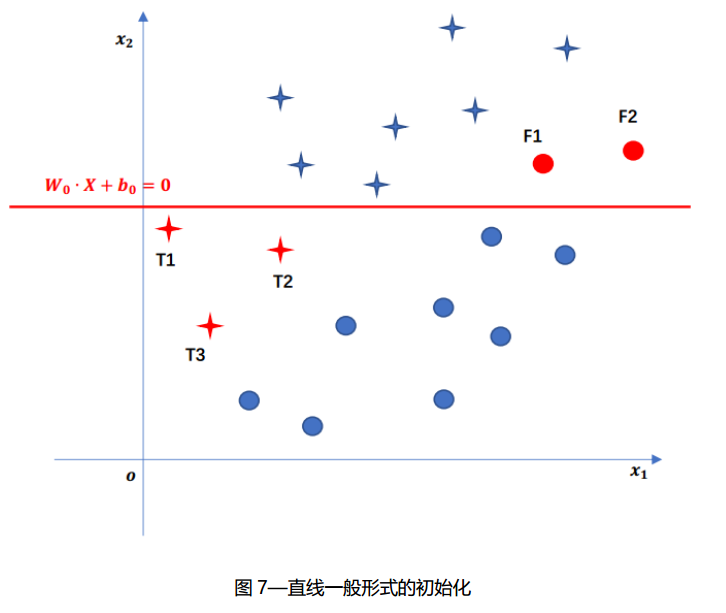
先还是随机挑选（随机初始化）一条直线 $ S_{0}: W_{0}∙X+b_{0}=0 $ , 在图中会发现一些误分类点（红色的圈点和叉点）。除了通过查看图像得出误分类点外，还可以通过点与直线的关系，确定一个代数表达式来计算验证某一点是否为误分类点。将点的坐标代入初始化直线所表示的感知机模型：$ f(X)=sign(W_{0}∙X+b_{0}) $ ,即可得到感知机模型根据输入X预测的类别f(X)，然后比较f(X)与数据点（X,y）中实际类别y是否相同即可。即 $ y∙sign(W_{0}∙X+b_{0})≤0 $
的点X就为误分类点。解决这些误分类点就成了感知机模型学习的关键。
图7中，在误分类点集合中，随机挑选一个点，假设挑选了点T1，坐标为 $ X_{T1} $ ，类别为 $ y_{T1} $ ，为了使感知机模型正确区分T1，需要对参数进行调整，更新。
图7中，T1的类别 $ y_{T1}=+1 $ , 而感知机模型的预测类别为 $ f(X_{T1} )=sign(W_{0}∙X_{T1}+b_{0} )=-1 $ ,说明，是式子 $ W_{0}∙X_{T1}+b_{0} $ 的值过小，所以，需要增大 $ W_{0} $ 和 $ b_{0} $ 的值。调整方式为：

$ W_{1}=W_{0}+ηX_{T1}, b_{1}=b_{0}+η; $

η为人为设置的参数（也称为学习率，表示参数更新的精度）；
同理，当 $ y_{T1}=-1 $时，调整方式为：

$ W_{1}=W_{0}-ηX_{T1}, b_{1}=b_{0}-η; $

小结上述过程，调整方式为：

$ W_{1}=W_{0}+ηy_{T1} X_{T1}, b_{1}=b_{0}+ηy_{T1}; $ 注：当然，某些时候，对于误分类点，一次参数调整后，仍不能够将其正确分类，需要对同一个点多次调整，直至该点被正确分类。然后，可以看出，人为设置的参数 $ η $ 关系到所选误分类点参数更新的次数，设置过小，则需要更新数次，效率低；设置过大，则会导致，参数更新的精度不够。 当模型能够将T1点正确分类后，如图-8。 

当根据一个误分类点调整完毕后，需要扫描整个数据集，重新验证一个误分类点集。然后，依次类推，逐步调整直线，直至数据集完全被正确划分。