9.朴素贝叶斯

本文由中山大学In+ Lab整理完成，转载注明出处

团队介绍 传送门

简介

　　贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，所以称为贝叶斯分类。而朴素贝叶斯是贝叶斯分类中的一种方法。它是在贝叶斯定理的基础上增加了一个特征条件独立的假设，从而形成了这个算法。

贝叶斯定理

　　上边我们提到了，朴素贝叶斯是以贝叶斯定理为基础的一种算法，那么我们就要先介绍一下，贝叶斯定理是什么？

　　在介绍贝叶斯公式之前，我们先来学习两个概念：

　　（1） 条件概率

　　设A,B是两个事件，且P(B)>0,则在事件B发生的条件下，事件A发生的条件概率（conditional probability)为：

P(A|B)=P(AB)/P(B)

　　（2）乘法公式

　　这个公式其实我们可以这样看，AB同时发生的概率为P(AB),它其实就等于B先发生,然后A发生，（或者A先发生然后B发生）。

　　所以，其实我们有：

P（AB）= P(A|B) P(B) = P(B|A) P(A)

　　将其转化一下，我们就可以得到条件概率中的公式：

P(A|B)=P(AB)/P(B)

P(B|A)= P(AB)/P(A)

　　接下来，我们再介绍贝叶斯公式，先来看贝叶斯定理的公式的一个简单的理解：

 

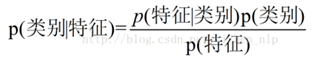
　　这其实就是贝叶斯公式的一个比较具体一点的表达，我们要做的就是根据给出的特征，判断它的类别，也就是p(类别|特征)。而根据我们的数据集，我们可以知道每一类的数据，它的特征的情况，以及每一类出现的概率，每种特征出现的概率，这些都可以根据我们已经有的数据来计算出来。具体可以看之后的例子。

　　有了对贝叶斯公式的简单理解之后，我们再来看一下真正的贝叶斯公式是怎样的。

　　下图即为贝叶斯定理的公式：

 

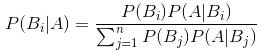
　　公式中，事件Bi的概率为P(Bi)，事件Bi已发生条件下事件A的概率为P(A│Bi)，事件A发生条件下事件Bi的概率为P(Bi│A)。

　　对于此式子，其中P(Bj) P(A│Bj)其实就是所有情况下A发生的概率，分母的取值其实就相当于P（A），简化一下，我们可以得到下边的式子：

 

　　这个形式就和我们本节开头的列子是一样的形式了，接下来我们就来看具体的例子来进行理解这个公式吧~

例题分析

         比如我们有如下股票数据：

        

股票ID	第一季度涨或跌	第二季度涨或跌	第三季度涨或跌	第四季度涨或跌	买不买
1	涨	涨	涨	涨	买
2	涨	跌	涨	涨	买
3	涨	涨	跌	涨	不买
4	跌	涨	跌	涨	不买
5	涨	涨	涨	跌	不买
6	跌	跌	跌	涨	买
7	跌	涨	涨	跌	买
8	涨	跌	跌	跌	不买
9	跌	跌	涨	涨	买
10	涨	涨	跌	涨	不买

        

         我们有四个特征，分别为四个季度，股票总体是涨了还是跌了。我们要做的是根据一只股票的特征来预测我们要不要买这只股票。

         假设我们现在有一只股票四个季度的特征为跌，涨，跌，涨，那么我们要不要买？

        

         这是一个典型的分类为题。

         转化为数学问题就是p（买|跌，涨，跌，涨）和p（不买|跌，涨，跌，涨）的概率，谁比较大，我就能确定到底买不买。

         这里我们就联系到贝叶斯公式：

         p（买|跌，涨，跌，涨）=

 

         这里我们需要求得是：p（买|跌，涨，跌，涨），但是我们可以利用贝叶斯公式转换为通过求其他三个量而得到我真正需要的值。

 

朴素一词解释

         上边我们说到了，可以通过求其他三个式子的值来得到我们想要的结果。那么这里我们就需要用到朴素贝叶斯了。

         我们如何求p（跌，涨，跌，涨|买）的结果呢？

         我们可以将它转换为p（跌1，涨2，跌3，涨4|买）= p（跌1|买）* p（涨2|买）* p（跌3|买）* p（涨4|买）。（为了区分，我将这里得特征名称分别加上代表季度的阿拉伯数字）

         这里，我们就有疑问了，这个等式如果要成立，不是需要特征之间相互独立吗？

         其实，这也正是朴素贝叶斯 “朴素” 的来源，朴素贝叶斯算法是假设各个特征之间互相独立，那么这个等式就成立了。

         但是，为什么我们需要假设特征之间互相独立呢？

 

         1、我们这么想，假如没有这个假设，那么我们对右边这些概率的估计其实是不可做的，这么说，我们这个例子有4个特征，四个特征均有涨，跌两种取值，那么四个特征的联合概率分布总共是4维空间，总个数为2*2*2*2=16个。

16个，计算机扫描统计还可以，但是现实生活中，往往有非常多的特征，每一个特征的取值也是非常之多，那么通过统计来估计后面概率的值，变得几乎不可做，这也是为什么需要假设特征之间独立的原因。

 

　　2、假如我们没有假设特征之间相互独立，那么我们统计的时候，就需要在整个特征空间中去找，比如统计p(跌1，涨2，跌3，涨4|买),我们就需要在买的条件下，去找四种特征全满足分别是跌，涨，跌，涨的股票的个数，这样的话，由于数据的稀疏性，很容易统计到0的情况，这样是不合适的。

 

　　根据上面两个原因，朴素贝叶斯法对条件概率分布做了条件独立性的假设，由于这是一个较强的假设，朴素贝叶斯也由此得名！这一假设使得朴素贝叶斯法变得简单，但有时会牺牲一定的分类准确率。

 

　　所以，我们的公式转化成了

　　p（买|跌，涨，跌，涨） =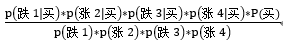 

        

例题详解

         那么我们接下来要做的就是一个个进行统计了。

 

         首先p（买） =？

        

股票ID	第一季度涨或跌	第二季度涨或跌	第三季度涨或跌	第四季度涨或跌	买不买
1	涨	涨	涨	涨	买
2	涨	跌	涨	涨	买
6	跌	跌	跌	涨	买
7	跌	涨	涨	跌	买
9	跌	跌	涨	涨	买

        

　　根据表格：p（买） = 5 / 10 = 1/2

　　p(跌1|买)=？

 

股票ID	第一季度涨或跌	第二季度涨或跌	第三季度涨或跌	第四季度涨或跌	买不买
6	跌	跌	跌	涨	买
7	跌	涨	涨	跌	买
9	跌	跌	涨	涨	买

 

　　根据表格：p(跌1|买)= 3/5

 

　　p(涨2|买)=？

股票ID	第一季度涨或跌	第二季度涨或跌	第三季度涨或跌	第四季度涨或跌	买不买
1	涨	涨	涨	涨	买
7	跌	涨	涨	跌	买

　　根据表格：p(涨2|买)= 2/5

 

　　p(跌3|买)=？

股票ID	第一季度涨或跌	第二季度涨或跌	第三季度涨或跌	第四季度涨或跌	买不买
6	跌	跌	跌	涨	买

　　根据表格：p(跌3|买)= 1/5

 

　　p(涨4|买)=？

股票ID	第一季度涨或跌	第二季度涨或跌	第三季度涨或跌	第四季度涨或跌	买不买
1	涨	涨	涨	涨	买
2	涨	跌	涨	涨	买
6	跌	跌	跌	涨	买
9	跌	跌	涨	涨	买

　　根据表格：p(涨4|买)= 4/5

 

　　接着，我们需要计算分母各项的值：

 

　　p(跌1)=？

股票ID	第一季度涨或跌	第二季度涨或跌	第三季度涨或跌	第四季度涨或跌	买不买
4	跌	涨	跌	涨	不买
6	跌	跌	跌	涨	买
7	跌	涨	涨	跌	买
9	跌	跌	涨	涨	买

　　根据表格：p(跌1)= 4/10 = 2/5

 

 

 

　　p(涨2)=？

股票ID	第一季度涨或跌	第二季度涨或跌	第三季度涨或跌	第四季度涨或跌	买不买
1	涨	涨	涨	涨	买
3	涨	涨	跌	涨	不买
4	跌	涨	跌	涨	不买
5	涨	涨	涨	跌	不买
7	跌	涨	涨	跌	买
10	涨	涨	跌	涨	不买

　　根据表格：p(涨2)= 6/10 = 3/5

 

　　p(跌3)=？

股票ID	第一季度涨或跌	第二季度涨或跌	第三季度涨或跌	第四季度涨或跌	买不买
3	涨	涨	跌	涨	不买
4	跌	涨	跌	涨	不买
6	跌	跌	跌	涨	买
8	涨	跌	跌	跌	不买
10	涨	涨	跌	涨	不买

　　根据表格：p(跌3)= 5/10 = 1/2

 

 

　　p(涨4)=？

股票ID	第一季度涨或跌	第二季度涨或跌	第三季度涨或跌	第四季度涨或跌	买不买
1	涨	涨	涨	涨	买
2	涨	跌	涨	涨	买
3	涨	涨	跌	涨	不买
4	跌	涨	跌	涨	不买
6	跌	跌	跌	涨	买
9	跌	跌	涨	涨	买
10	涨	涨	跌	涨	不买

　　根据表格：p(涨4)= 7/10

 

　　所以我们可以得到：

　　p（买|跌，涨，跌，涨） = 8/35

　　同理

　　P（不买|跌，涨，跌，涨） = 16/35

 

　　所以，答案就是 不买！

 

 

 

 

朴素贝叶斯的优缺点

　　优点：

　　　　（1） 算法逻辑简单,易于实现（算法思路很简单，只要使用贝叶斯公式转化即可！）

　　　　（2）分类过程中时空开销小（假设特征相互独立，只会涉及到二维存储）

 

　　缺点：

　　　　理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。

 

　　而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。