算法导论-----图论-----深度优先搜索及课后题答案
深度优先搜索
1.深度优先搜索先辈子图
Gπ=(V,Eπ),其中
Eπ={(π[v] ,v): v属于V且π[v]!=NIL}
2.加盖时间戳
每个顶点v有两个时间戳,当顶点v第一次被发现时(置为灰色),记录第一个时间戳d[v];当顶点第二次被发现时,置第二个时间戳f[v]
(灰色的都是栈里边的)
3.对|V|中顶点的每一个,都对应一个发现事件和完成事件,每一个顶点u都有d[u]<f[u]。这些时间戳为1到2|V|之间的整数。顶点u在时刻d[u]之前为白色,在时刻d[u]与d[v]之间为灰色。在以后就变成黑色了
4.time 是一个全局变量,用于记录时间戳,DFS时间复杂度O(V+E)
DFS(G)
For each vertex u 属于V[G]
Do color[u]=white
π[u]=NIL
time =0;
for each vertex u 属于V[G]
do if color[u]=white
then DFS-VISIT(u)
DFS-VISIT(u)
color[u]=gray
timeßtime+1
d[u]=time
for each v 属于adj[u]
do if color[v]=white
thenπ[v]=u
DFS-VISIT(v)
color[u]=black
f[u]ßtimeßtime+1
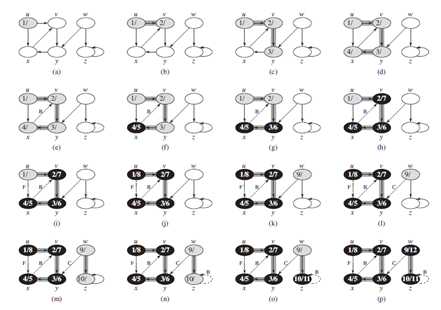
5.深度优先搜索的性质
(1) DFS中顶点v是u的后裔,当且仅当v是u为灰色时发现的
(2)如果发现顶点u用左括号(u来表示,完成用右括号u)来表示,在各级括号正确嵌套的前提下,发现与完成时间的记载就是一个完善的表达式
(3) 括号定理:在对一个(有向或无向)图G=(V,E)的任何深度优先搜索中,对于图中的任意两个顶点u,v下列三个条件仅有一个成立
(a)区间[d[u],,f[u]]和区间[d[v],f[v]]是完全不相交的,v或u都不是对方的后裔
(b)区间[d[u],f[u]]完全包含于区间[d[v],f[v]],且在深度优先树中u是v的后裔
(c)区间[d[v],f[v]]完全包含于区间[d[u],f[u]],且在深度优先树中v是u的后裔
(4) 后裔区间嵌套
在一个有向或无向图G=(V,E)中,顶点v是顶点u的后裔,当且仅当d[u]<d[v]<f[v]<f[u]
(5) 白色路径定理
在一个有向或无向图G=(V,E)的深度优先森林中,顶点v是顶点u的后裔,当且仅当在搜索过程中与时刻d[u]发现u是,可以从顶点u除法,经过一条完全有白色顶点组成的路径到达v
(6)u,v是一条
a)树边或前向边,当且仅当d[u]<d[v]<f[v]<f[u]
b)反向边,当且仅当d[v]<=d[u]<f[u]<=f[v]
c)交叉边,当且仅当d[v]<f[v]<d[u]<f[u]
6.对边的分类
(1)树边:在深度优先森林Gπ总共的边,如果顶点v是探寻边(u,v)时首次被发现的,那么(u,v)就是一条树边
(2)反向边:深度优先树中,连接顶点u到它的某一祖先的那些边。有向图出现的自环也是反向边
(3)正向边:在深度优先搜索中,连接u和某个后裔的非树边(u,v)
(4)交叉边:同一棵深度优先搜索树的两个顶点之间,条件是其中一个顶点不是另一个顶点的祖先。也可以在不同度优先搜索树之间的顶点之间
7.对边分类的算法
对于每一条边(u,v),当该边被第一次探寻到时,即根据所到达的顶点v的颜色来对该
边进行分类
(1)白色 表明它是一条树边
(2)灰色 表明它是一条反向边
(3)黑色 d[u]<d[v]则(u,v)就是一条正向边
(4)d[u]>d[v]则(u,v)就是一条交叉边
8.在对一个无向图G进行深度优先搜索时,G的一条边要么是树边,要么是反向边
(不可能出现正向边和交叉边)(想想为什么)
所以在无向图的的深度优先搜索中先发现(白色)的为树边
后发现的(灰色)为反向边。另外,不可能发现黑色的点,想想为什么
9.课后习题22.3-6
DFS(G)
For each vertex u in V
color[u]=white
pi[u]=nil
time=0
for each vertex u in V
if color[u]=white
DFS-Vist(u)
DFS-Visit(u)
color[u]=gray
time++
d[u]=time
push(u)
while stack not empty
u=top()
isleaf=true
for each v int adj[u]
if color[v]=white
color[v]=gray
pi[v]=u
time++
d[v]=time
push(v)
isleaf=false
break;
if isleaf=true
color[u]=black
time++
f[u]=time
pop()
10.课后题22.3-7和22.3-8的反例
11.课后题22.3-9
DFS(G)
For each vertex u 属于 V[G]
Do color[u]=white
pi[u]=NIL
timeß0
for each vertex u 属于V[G]
do if color[u]=white
then DFS-VISIT(u)
DFS-VISIT(u)
color[u]=gray
d[u]ßtimeßtime+1
for each vertex v 属于 adj[u]
do if(color[u]=gray)
if directed(G) or v!=pi[u]
then print(u,v)"is a back-edge"
else if directed(G) and color[v]=BLACK
then if d[u]<d[v]
then print(u,v) "is a forward-edge"
else print(u,v)"is a cross-edge"
else if color[v]=white
then pi[v]ßu
print(u,v) "is a tree-edge"
DFS-VISIT(v)
color[u]=black
f[u]ßtimeßtime+1
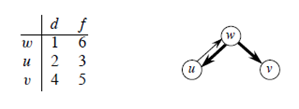
12.课后题22.3-10
从w,u,v分别开始DFS

13-课后题22.3-11
DFS(G)
For each vertex u 属于 V[G]
Do color[u]=white
pi[u]=NIL
timeß0
counterß0
for each vertex u 属于 V[G]
do if color[u]=white
then counterßcounter+1
DFS-Visit(u,counter)
DFS-VISIT(u,counter)
color[u]=gray
cc[u]=counter
timeßtime+1
d[u]ßtime
for each v 属于 adj[u]
do if color[v]=white
then pi[v]ßu
DFS-VISIT(v,counter)
color[u]=black
f[u]ßtimeßtime+1
14.课后习题22.3-12
判断单连通图
单连通图:对任意两个顶点u,v属于V,则至多只有一条从u到v的简单路径
若为单连通图,u,v只能是树边和反向边,不能是前向边和交叉边
DFS(G)
timeß0
For each vertex u属于V[G] //对每个顶点都判断是否是单连通
Do
{
For each vertex v 属于V[G]
{
color[v]=white
pi[v]=nil
}
DFS-VISIT(u)
}
Print "G is singly connected"
DFS-visit(u)
{
color[u]=gray
timeßtime+1
d[u]ßtime
for each v 属于adj[u]
do if color[v]=white
then pi[v]=u
DFS-visit(v)
else if color[v]=black
then print "G is not singlu connected"
return
color[u]=black
f[u]ßtimeßtime+1
}


