算法导论-----数论-----求解模线性方程
-
ax=b(modn)
设<a>是模n加法群中的循环子群，即<a>={
}={axmodn}，所以有一个解当且仅当b属于<a>，而|<a>|必定是n的约数 -
对任意正整数a,n，若d=gcd(a,n),在
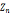中 <a>=<d>={0,d,2d,3d…(n/d-1)d}所以|<a>|=n/d;
证明：(1)<d>属于<a>
ax+ny=d,ax=d(modn),d的倍数属于a
(2)<a>属于<d>
设m属于<a>
ax=m(modn),ax+ny=m,d|ax+ny,d|m,m属于<d>
- ax=b(modn)有解，当且仅当gcd(a,n)|b
-
ax=b(modn)或者无解，或者对模n有d=gcd(a,b)个不同的解
证明有d个不同的解：
若在<a>中有一个解，则，由于|<a>|=n/d,所以重复d次
-
设d=gcd(a,n)，d=ax`+ny`，若d|b,则方程ax=b(modn)的一个解x0满足
x0=x`(b/d)(modn)
证明：ax0=ax`(b/d)(modn)
ax0=d(b/d)(modn)
-
方程ax=b(modn)有解（即d|b，其中d=gcd(a,n)）x0是方程任意一个解，方程有d个不同的解，分别为xi=x0+i(n/d) (i=1,2,…,d-1)
证明：
axi(modn)=a(x0+i(n/d))(modn)
=ax0(modn)=b(modn)
-
MODULAR-LINEAR-EQUATION-SOLVER(a,b,n)
{
(d,x`,y`)=EXTEND-EUCLID(a,n)
if(d|b)
{
x0=x`(b/d)(modn)
for(i=0 to i-1)
print x0+i(n/d)(modn)
}
else
print "no solution"
}
时间复杂度 lg(b)
- n>1,gcd(a,n)=1,则ax=b(modn)有唯一解
- n>1,gcd(a,n)=1,则ax=1(modn)有唯一解，否则方程无解
