Poj 2480
求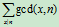
，1<=x<=n
可转化为n的每一个约数，乘以，1~n内与n的最大公约数为此约数个数，再求和。
- 求n的约数。
- 求个数。设a为n的一个约数，求满足gcd(x,n)=d，x的个数
gcd(x/d,n/d)=1,所以乘法群n/d的规模为phi(n/d),即x有phi(n/d)个
求n的约数
继续简化问题
设n=
设f(n)为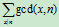
所以f(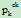
) =
=
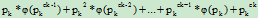
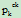*(1-1/pk)+ 
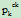*(1-1/pk)+…+
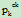*(1-1/pk)+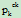 
=ek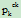
(1-1/pk)+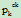 
Gcd为积性函数，所以和函数f也为积性函数
f(n)=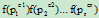 
=n*…(ek (1-1/pk)+1)*…
方法一:47MS，每次循环都求素数因子
#include <iostream>
#include <stdio.h>
using namespace std;
long long eu(long long n)
{
long long ret=n,e,i;
for(i=2;i*i<=n;i++)
{
if(n%i==0)
{
e=0;
while(n%i==0){n/=i;e++;}
ret=ret/i*e*(i-1)+ret;
}
}
if(n>1)
ret=ret/n*(2*n-1);
return ret;
}
int main()
{
long long n;
freopen("in.txt","r",stdin);
while(scanf("%lld",&n)!=EOF)
printf("%lld\n",eu(n));
return 0;
}
方法二，16ms，打印素数表
#include <iostream>
#include <stdio.h>
using namespace std;
const int MAX=65535;
bool prime[MAX+10];
int a[MAX+10];
void getprime()
{
long long i,j;
int cnt=1;
prime[0]=prime[1]=0;
for(i=2;i<=MAX;i++)
prime[i]=1;
for(i=2;i<=MAX;i++)
{
if(prime[i])
{
a[cnt++]=i;
for(j=i*i;j<=MAX;j+=i)
prime[j]=0;
}
}
}
long long eu(long long n)
{
long long ret=n,e,i;
for(i=1;a[i]!=0&&a[i]*a[i]<=n;i++)
{
if(n%a[i]==0)
{
e=0;
while(n%a[i]==0){n/=a[i];e++;}
ret=ret/a[i]*e*(a[i]-1)+ret;
}
}
if(n>1)
ret=ret/n*(2*n-1);
return ret;
}
int main()
{
long long n;
getprime();
freopen("in.txt","r",stdin);
while(scanf("%lld",&n)!=EOF)
printf("%lld\n",eu(n));
return 0;
}
