算法导论-----数论-----最大公约数

1.p1p2…pr为素数

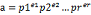
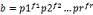
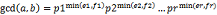
2. gcd(a,b)=gcd(b,amodb)

证明：(1)证gcd(a,b)|gcd(b,amodb)

         令d=gcd(a,b)

            d|a,d|b,a=b+amodb,amodb=a-b,所以d|amodb所以~

(2)证gcd(b,amodb)|gcd(a,b)

令d=gcd(b,amodb)

        a=b+amodb,所以~

3.EUCLID(a,b)

{

        If(b==0)

return 0;

        else

            return EUCLID(b,amodb);

}

4.若a>b>=1且EUCLID(a,b)执行了k>=1次递归调用，则a>=Fk+2,b>=Fk+1(用数学归纳法证明)

5.Lame定理：k>=1,a>b>=1,b<fk+1,则EUCLID执行递归少于k次

gcd(fk+1,fk)=gcd(fk,fk-1);EUCLID(fk+1,fk)恰好进行k-1次调用

6.EXTEND-EUCLID(a,b)

{

        If(b==0)

            return (a,1,0);

        (d`,x`,y`)=EXTEND-EUCLID(b,amodb);

        (d,x,y)=(d,y`,x`-(a/b)y`);

        return (d,x,y);

}

时间复杂度 log(b);

7.d`=bx`+(amodb)y`;

d=bx`+(amodb)y`=ay`+b(x`-(a/b)y`);