[Leetcode 1631]最少体力消耗的路径Path With Minimum Effort

题目

https://leetcode.com/problems/path-with-minimum-effort/

每个节点的height不同，矩阵从左上走到右下，求最小体力消耗

当前点体力消耗：max（来的那个节点的effort，|来的那个节点height-当前节点height|）

总最小体力消耗：所选路径加起来

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

 

Example 1:

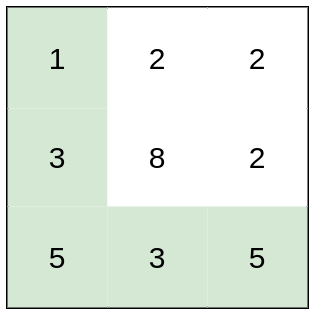
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

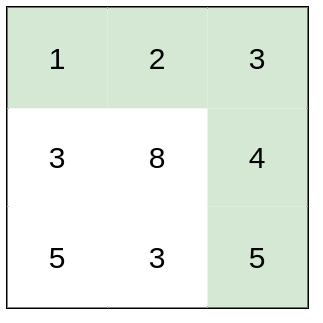
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

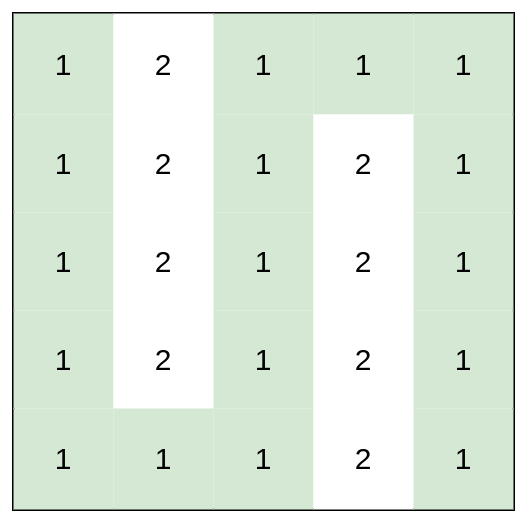
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

 

 

思路

dijktra+优先队列

迪杰斯特拉算法：https://www.bilibili.com/video/BV1zz4y1m7Nq

dijktra可以理解成一种BFS，即向相邻节点搜索，

eg 到第i个节点，比较（到第i-1个节点的长+去第i个节点的长）和（第0个节点直接到第i个节点的长）

如果更小，就更新路径，并记录在是从i-1节点过来的

 

优先队列主要是理解comparator比较器的设置，参考相关priorityqueue的题

代码

 

class Solution {
    final int[][] direction={{-1,0},{1,0},{0,-1},{0,1}};
    public int minimumEffortPath(int[][] heights) {
        int m=heights.length;
        int n=heights[0].length;
        int[][] cost=new int[m][n];//动态的存储到每个点的最小effort
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                cost[i][j]=Integer.MAX_VALUE;//先全部设为极大值，后面更新
            }
        }
        cost[0][0]=0;//起始点

        //pq设置根据【位置2】（cost）升序排列，即小的在前
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(a[2], b[2]));
        pq.offer(new int[]{0,0,0});//{点n的x位置,点n的y位置,cost}，即到这个点的最小effort

        while(!pq.isEmpty()){
            //取出目前走到的矩阵位置
            int[] cur=pq.poll();
            int i=cur[0];
            int j=cur[1];
            
            //如果已经走到右下角，返回结果
            if(i==m-1&&j==n-1)
                break;
            
            //反之，朝上下左右4个direction试探
            for(int[] dir:direction){
                //下一步，试探的位置
                int x=i+dir[0];
                int y=j+dir[1];
                //如果越界
                if(x<0||y<0||x>=m||y>=n){
                    continue;
                }
                //试探位置的cost计算，最大effort
                //取俩者大的 上一步cost即cur[2]，试探位置与试探位置的绝对值
                int curCost=Math.max(cur[2],Math.abs(heights[x][y]-heights[i][j]));
                if(curCost<cost[x][y]){
                    //pq.offer(new int[]{x,y,curCost});//这里有问题
                    cost[x][y]=curCost;//要记得更新cost！！不然一直是MAX_VALUE
                    
                    //更新pq
                    pq.offer(new int[]{x,y,curCost});
                }
            }
        }
        
        //返回到右下角这个点的min effort
        return cost[m-1][n-1];
    }
}