《Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments》论文解读
目录
一、摘要
文章探索了多智能体(multi-agent)领域的强化学习方法。
由于多智能体的环境状态由多个agent的行为共同决定,本身具有不稳定性(non-stationarity),Q-learning算法很难训练,policy gradient算法的方差会随着智能体数目的增加变得更大。
作者提出了一种actor-critic方法的变体MADDPG,对每个agent的强化学习都考虑其他agent的动作策略,进行中心化训练和非中心化执行,取得了显著效果。此外在此基础上,还提出了一种策略集成的训练方法,可以取得更稳健的效果(Additionally, we introduce a training regimen utilizing an ensemble of policies for each agent that leads to more robust multi-agent policies.)。
二、效果展示
- 追捕环境
四个红色的agent追捕两个绿色的agent获得回报。绿色的agent躲避追捕,到达蓝色点(表示水源)处获得回报。黑色点表示障碍物。
![]()
在上述环境中,MADDPG分别训练了图中四个红色的agent和两个绿色的agent。可以看到,红色agent已经学会了组队追捕绿色agent,同时绿色agent也学会了分散躲避追捕并跑向蓝色点。 - MADDPG与DDPG效果比较
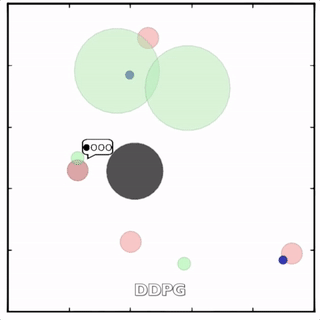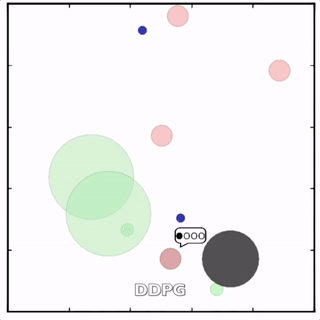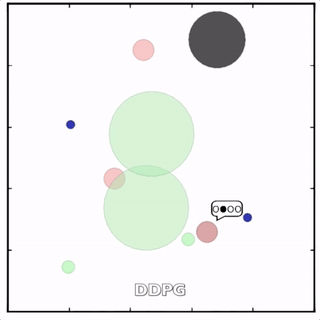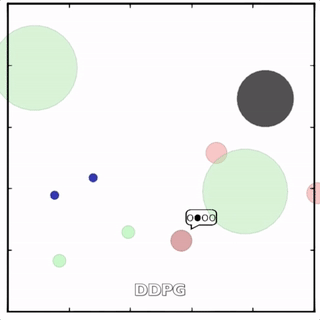
该环境也是追捕环境,其中浅绿色大圆表示森林,其他含义同上。其中一个红色agent貌似负责总体指挥(含义不明)。
![]()
![]()
其中红色agent分别用MADDPG和DDPG训练得到,其中MADDPG训练得到的agent捕获了更多的绿色agent,也更会合作。
三、方法细节
- 问题分析
传统强化学习方法很难用在multi-agent环境上,一个主要的原因是每个agent的策略在训练的过程中都是不断变化的,这导致对每个agent个体来说,环境都是不稳定的,即有\(P(s'|s,a,\pi_1,...,\pi_N) \not = P(s'|s,a,\pi_1',...,\pi_N')\)对任意的\(\pi_i \not = \pi_i'\)。某种程度上来说,一个agent根据这种不稳定的环境状态来优化策略是毫无意义的,在当前状态优化的策略在下一个变化的环境状态中可能又无效了。这就导致不能直接使用经验回放(experience replay)的方法进行训练,这也是Q-learning失效的原因。对于policy gradient方法来说,随着agent数量增加,环境复杂度也增加,这就导致通过采样来估计梯度的优化方式,方差急剧增加。作者还证明了在一个包含\(N\)个agent的二值动作空间上,假设\(P(a_i=1)=\theta_i,\ where\ \ R(a_1,...,a_N)=\textbf1_{a_1=...=a_N}\),取\(\theta_i=0.5\),那么梯度估计方向的正确性正比于\(0.5^N\),即\(P(\langle \hat{\nabla} J,\nabla J\rangle>0)\propto (0.5)^N\)。其中\(\hat{\nabla} J\)是估计梯度,\(\nabla J\)是真实梯度。(PS:我仔细看了这个证明,表述有一点瑕疵,但结论是对的,我写在最后帮助大家理解。)
这些问题归根到底,是因为agent之间没有交互,不知道队友或者对手会采取什么策略,导致只根据自己的情况来选择动作,而忽略了整体。作者提出的解决方法也很简单:采用中心化的训练和非中心化的执行。即在训练的时候,引入可以观察全局的critic来指导actor训练,而测试的时候只使用有局部观测的actor采取行动。
此外作者还采取了两种改进方式,个人感觉不是重点。1. 不假设训练的时候知道其他agent的策略,而是通过预测的方式获得。2. 采用策略集成的方法提升稳定性。 - 具体方法
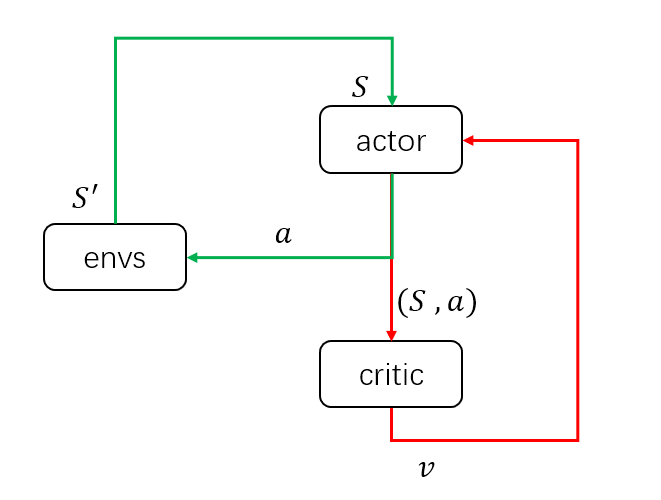
该方法和DDPG方法其实很类似,这里先画一个简图来说明DDPG结构的输入输出:![]()
当策略训练好后,只需要actor与环境交互,即只需要绿色的循环,其中actor的输入为环境状态\(S\),输出为具体动作\(a\)。而在训练过程中,需要critic获得当前的环境状态和actor采取的动作,组成状态动作对\((S,a)\)作为输入,输出状态动作对的价值\(v\)来评估当前动作的好坏,并帮助actor改进策略。这里首先假设对DDPG有了解,不细说更新方法。具体推荐博客:
Deep Reinforcement Learning - 1. DDPG原理和算法
深度强化学习——连续动作控制DDPG、NAF
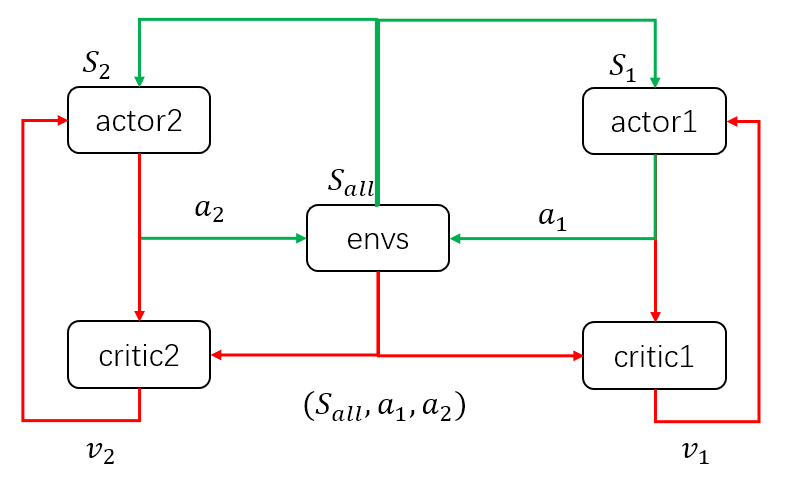
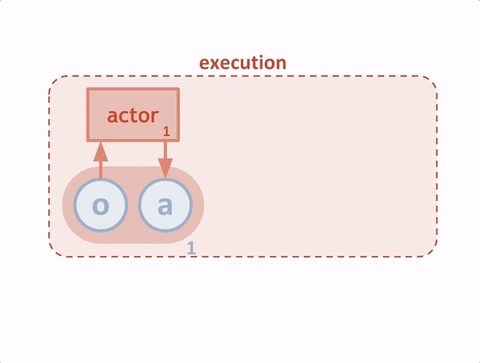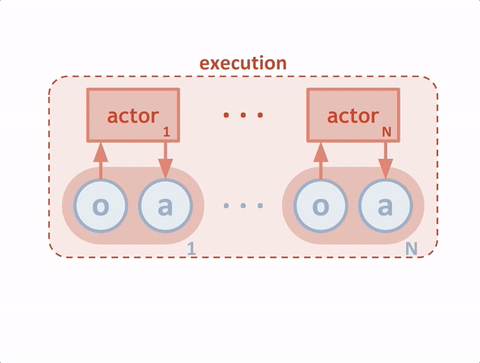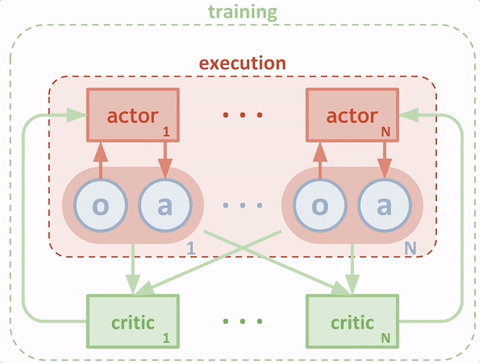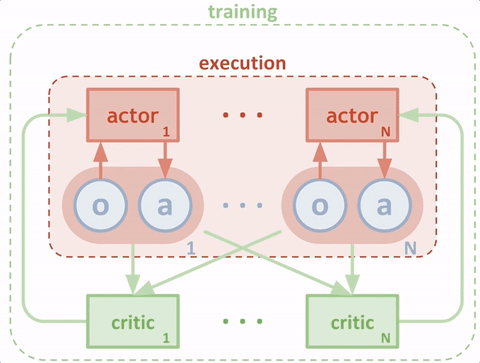
说清楚了DDPG的输入输出,MADDPG就很清楚了。以两个agent为例,同样画出输入输出的简图如下:![]()
当模型训练好后,只需要两个actor与环境交互,即只需要绿色的循环。这里区别于单个agent的情况,每个agent的输入状态是不一样的。环境输出下一个全信息状态\(S_{all}\)后,actor1和actor2只能获取自己能够观测到的部分状态信息\(S_1,S_2\)。而在训练过程中,critic1和critic2可以获得全信息状态,同时还能获得两个agent采取的策略动作\(a_1,a_2\)。也就是说,actor虽然不能看到全部信息,也不知道其他actor的策略,但是每个actor有一个上帝视角的导师,这个导师可以观测到所有信息,并指导对应的actor优化策略。![]()
整个过程为中心化的训练和去中心化的执行。这种改进,理论上将之前环境不稳定的问题得以缓解。即\(P(s'|s,a,\pi_1,...,\pi_N) \not = P(s'|s,a,\pi_1',...,\pi_N')\)对任意的\(\pi_i \not = \pi_i'\)。转变为\(P(s'|s,a_1,...,a_N,\pi_1,...,\pi_N)=P(s'|s,a_1,...,a_N)=P(s'|s,a_1,...,a_N,\pi_1',...,\pi_N')\ \ for\ any\ \pi_i \not=\pi_i'\)。 - 伪代码
我们放上MADDPG和DDPG的伪代码进行比较。
![]()
![]()
可以很明显的看到,从actor网络的初始化和噪声扰动方法,到critic网络的更新方法,以及actor网络的梯度提升方法,最后target网络的更新,几乎一模一样。唯一的区别就在于\(Q\)函数的输入从单个的动作\(a\)变成了所有agent的动作\(a_1,a_2,...,a_N\)。 - 网络结构
作者使用了最简单的两层全连接和relu激活函数,每层64个神经元。对于离散动作的场景使用了Gumbel-Softmax进行估计。优化器Adam,学习率0.01,\(\tau=0.01,\gamma=0.95\),replay buffer \(10^6\),batch size 1024。
到此,方法介绍完毕。
四、实验结果
- 其他环境效果展示
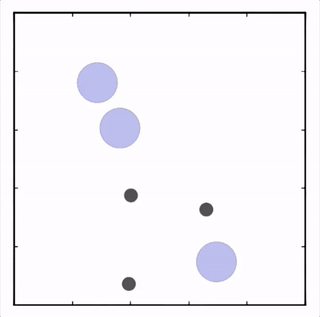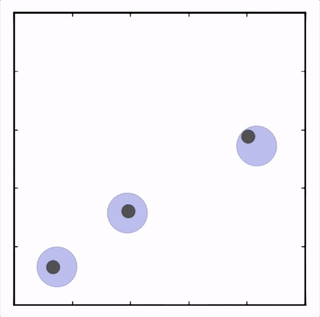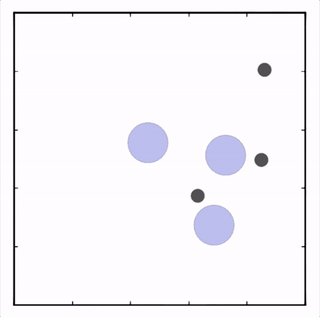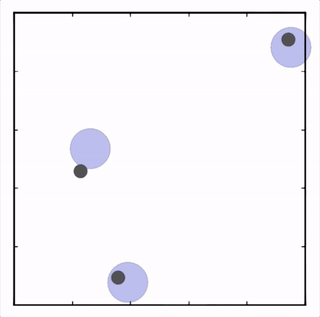
- Physical deception
两个紫色agent合作到达一个地方(只要一个agent到达即可),同时掩饰他们的真正目的地以迷惑对手。![]()
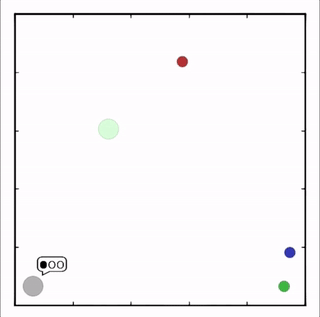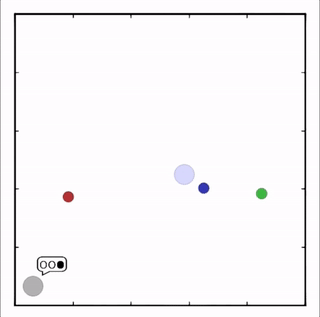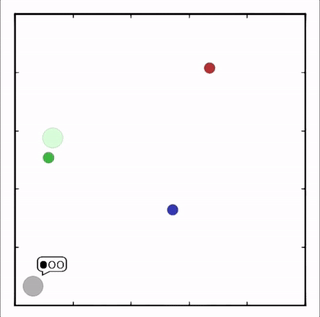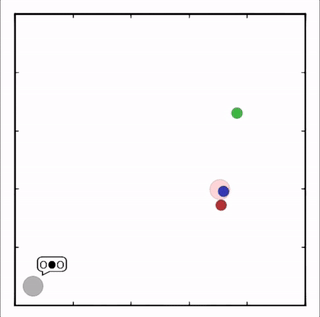
- Cooperative communication
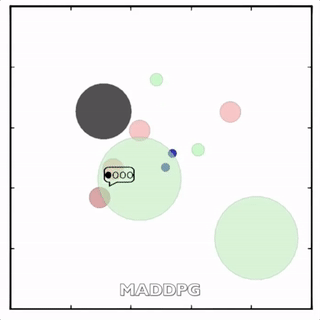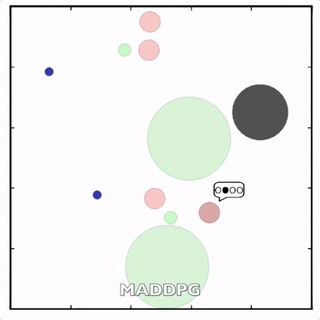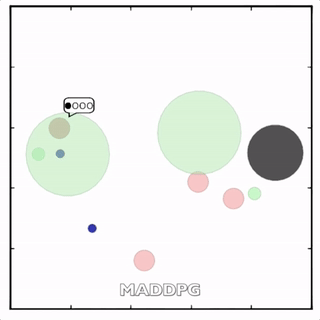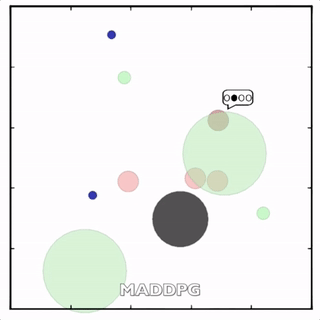
灰色agent告诉agent需要到达的目标,另一个agent执行。![]()
- Cooperative navigation
三个agent分别到达不同目标获得最大回报。![]()
- Physical deception
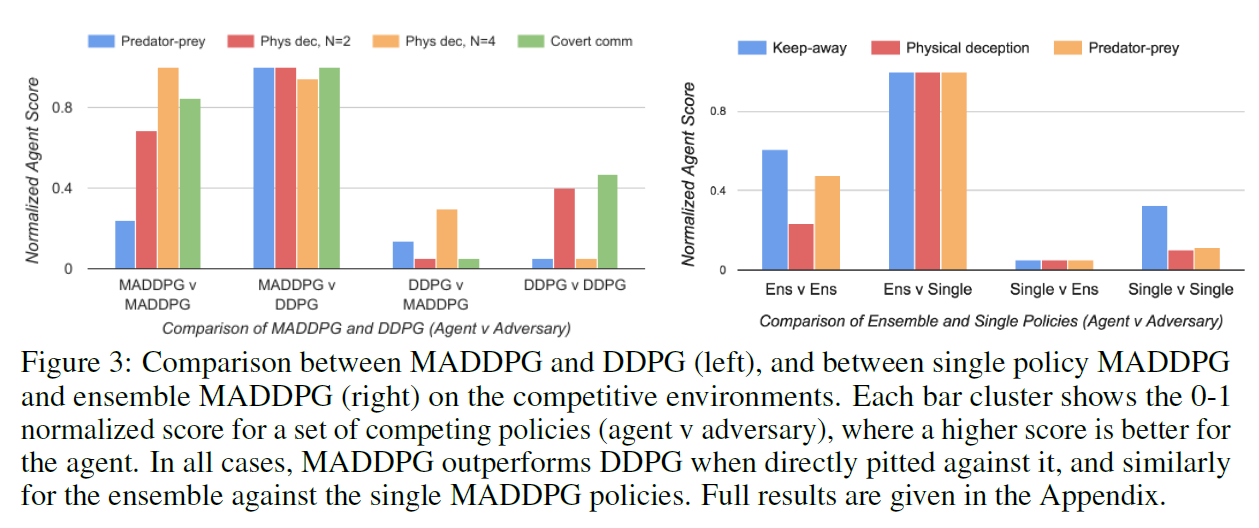
- MADDPG、DDPG效果比较
在多个环境中分别用MADDPG的agent对抗DDPG的agent,得分如下图。![]()
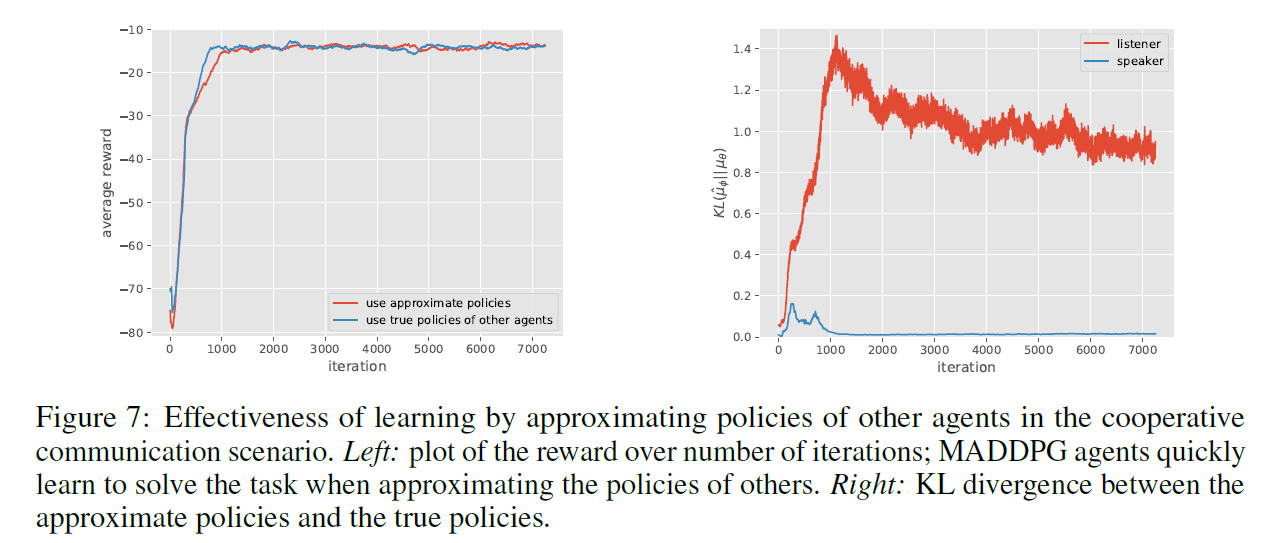
- 策略预测效果
作者尝试了通过训练的方式去预测其他agent的动作,再用来计算Q值,而不是直接给critic真正的动作值。发现可以达到同样的合作效果,但是另一方面动作预测的效果其实很不理想。这就有点让人费解了,到底是什么原因使得agent之间学会合作的?![]()
- 其他
其他实验结果具体参考原论文。
五、总结
这篇文章效果显著,思想也顺理成章,文章还证明了policy gradient方法失效的原因。
但我个人从另一方面YY,这个方法思想浅显且效果显著,其他学者应该也想到了类似方法,最终却没有做出效果,可见这其中的trick应该不少。另外上述的策略预测效果的实验结果图,也间接说明了其他agent的策略信息对训练有多少实质性的帮助并不清楚。
附录
- Proposition 1
先把证明原文打出,再解释其中一些问题![]()
![]()
前面部分只是一些小瑕疵,最费解的是最后一步,这里依次列一下。
- (10)中第二个等式少了一个括号,应该为\(R(a_1,...,a_N)\frac{\partial}{\partial\theta_i}\sum\limits_i(a_i\log\theta_i+(1-a_i)\log(1-\theta_i))\)
- For \(\theta_i=0.5\) we have:\(\frac{\hat{\partial}}{\partial\theta_i}J=R(a_1,...,a_N)(2a_i-1)\) 应为\(\frac{\hat{\partial}}{\partial\theta_i}J=R(a_1,...,a_N)(4a_i-2)\),只有当后面的假设\(R(a_1,...,a_N)=\textbf1_{a_1=...=a_N=1}\)成立时,才有前面的式子。
- 求期望的式子中,\(E(R)\)是关于动作\(a\)的期望,而之后\(E(\frac{\hat{\partial}}{\partial\theta_i}J)\)是关于参数\(\theta\)的期望
- 最后一步
We have:\(\langle\hat{\nabla J,\nabla J}\rangle=\sum\limits_i\frac{\hat{\partial}}{\partial\theta_i}J\times(0.5)^N=(0.5)^N\sum\limits_i\frac{\hat{\partial}}{\partial\theta_i}J\),so \(P(\langle \hat{\nabla}J,\nabla J\rangle>0)=(0.5)^N\).
这里是最让人迷惑的地方,最开始我一直以为这里的因果关系so是因为前面的系数\((0.5)^N\)。但是转念一想这个\(\langle \hat{\nabla}J,\nabla J\rangle>0\)的概率和系数\((0.5)^N\)是无关的,不管\(N\)是多少\((0.5)^N\)只是乘在前面的一个大于0的常数,不影响两个梯度内积的正负。后来终于明白,这个概率的关系来自第二项\(\sum\limits_i\frac{\hat{\partial}}{\partial\theta_i}J\)。
由前面可知,当\(R(a_1,...,a_N)=\textbf1_{a_1=...=a_N=1}\)时,有\(\frac{\hat{\partial}}{\partial\theta_i}J=R(a_1,...,a_N)(2a_i-1)\),则\(\sum\limits_i\frac{\hat{\partial}}{\partial\theta_i}J=\sum\limits_i R(a_1,...,a_N)(2a_i-1)\)。注意看这个式子,虽然是\(N\)个回报的和,但是要想这个求和大于0的唯一解只有当\(a_1=a_2=...=a_N\)时,其他时候回报都为0。也就是说这个求和其实只有两个值,要么为0要么为\(N\)。
而每个\(a_i\)是一个伯努利分布且独立,所以\(a_1=a_2=...=a_N=1\)的概率即相当于求二项分布\(X=\sum\limits_ia_i\)使得\(X=N\)的概率。又二项分布概率公式为\(P(X=k)=\binom{N}{k}p^k(1-p)^{N-k},\ \ where\ \ (p=0.5,k=0,...,N)\)。则有\(P(X=N)=(0.5)^N\),这才得到前面的so,\(P(\langle \hat{\nabla}J,\nabla J\rangle>0)=(0.5)^N\)。
- (10)中第二个等式少了一个括号,应该为\(R(a_1,...,a_N)\frac{\partial}{\partial\theta_i}\sum\limits_i(a_i\log\theta_i+(1-a_i)\log(1-\theta_i))\)









 浙公网安备 33010602011771号
浙公网安备 33010602011771号