The Second Type of Uncertainty in Monte Carlo Tree Search
发表时间:2020
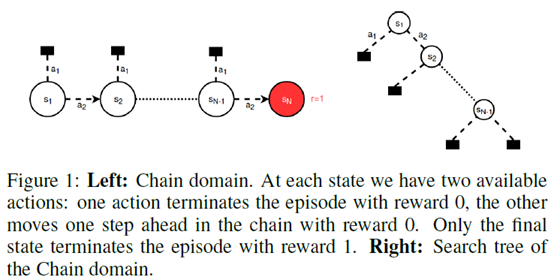
文章要点:MCTS里通常通过计算访问次数来做探索,这个被称作count-derived uncertainty。这篇文章提出了第二种uncertainty,这种uncertainty来源于子树的大小,一个直觉的想法就是,如果一个动作对应下的子树小,那就不用探索那么多次,反之如果子树大,那就应该多探索探索。作者提出了MCTS-T和MCTS-T+算法,在树里添加度量子树大小的估计(estimate of the size of the subtree below an action),在稀疏回报的场景以及有loop的场景下取得了很好的效果。
具体的,作者定义每个状态的uncertainty \(\sigma_{\tau}(s) \in [0,1]\),其中1表示这个状态下的子树完全没探索过,0表征这个子树已经被探索完全了。所以在初始化的时候,只有终结状态被设置为0,其他状态都被设置为1

然后更新的公式也是通过计算访问次数然后根据backup的uncertainty来算平均值
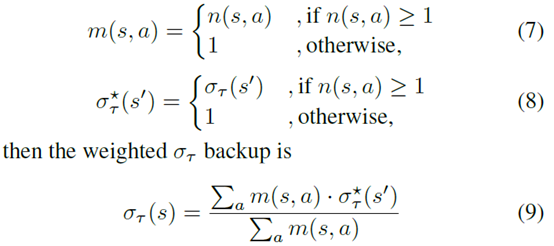
然后select的公式就变成
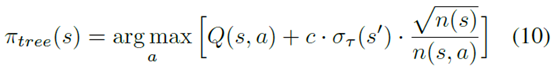
这个uncertainty以乘积的形式放到exploration那一项上。
另外一个需要注意的问题是,如果一个很大的子树的value都很差,但是因为uncertainty很大,那么访问次数就会很多,这样就会导致value更新不准,所以value的更新不能依据这个访问次数去做。作者的做法是依然保留一个和原版MCTS一样的访问次数的计算,就是如果新的select公式选择的动作和原版MCTS选择的动作一样,就算一次访问次数
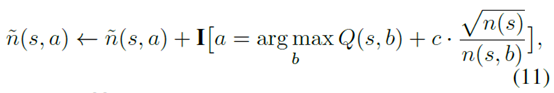
然后用这个访问次数去更新value

另外一个需要解决的问题是Loops,也就是说在一次搜索中,search可能在几个动作之间来回横条,这就导致这个树变的平衡了,但是其实都是在相同几个状态之间来回跳,其实相当于没用
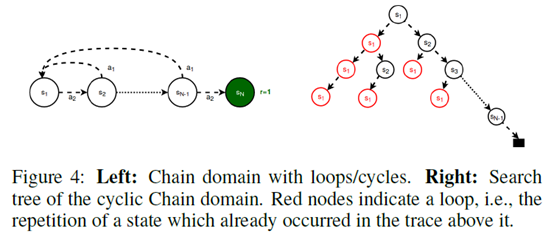
作者的做法也很直接,就是在一次搜索中,如果在后面的节点遇到了之前相同的状态,就把这个地方的uncertainty设置为0,那么就会避免相同状态反复横跳了。如果状态空间太大,还可以设置阈值来做近似的判断

而且注意这个方式是MCTS的扩展,如果没到terminal状态,所有的select,backup就和MCTS完全一样。
总结:很有意思的想法,感觉是不是可以试试结合到神经网络上面去。另外,目前做的还是确定性转移的情形。
疑问:如果有随机转移,会不会错误block掉很多loops?
另外如果一个游戏就是反复横跳得分最高,是不是效果也会差一点?



 浙公网安备 33010602011771号
浙公网安备 33010602011771号