Discretizing Continuous Action Space for On-Policy Optimization
发表时间:2020(AAAI 2020)
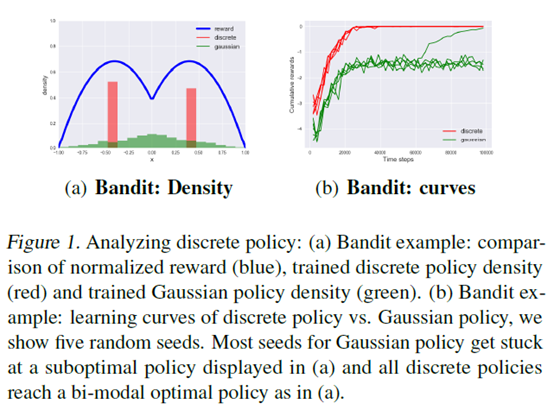
文章要点:作者想说,连续动作通常都假设每个维度是高斯分布的,这就限制了策略一定是一个单峰,而离散动作就没有这个约束,所以有离散的必要。然后这篇文章提出了一个把连续动作空间离散化的方法,同时避免维度爆炸。通常如果一个连续空间有\(M\)个维度,如果我每一维都离散成\(K\)个动作,那就有\(K^M\)个动作组合(文章里说有\(M^K\)个,感觉不太对),这就太大了。作者定义了一个动作离散的方式,对每个维度的动作,我有
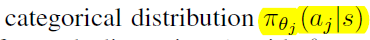
然后整个policy可以写成
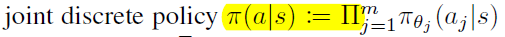
就相当于每个维度单独考虑,不联合起来考虑(To overcome the curse of dimensionality, we represent the distribution as factorized across dimensions.)。
同时,还假设每个维度下离散的动作是有顺序的,比如在某个状态动作取0.5的时候Q value很高,那我合理猜测在0.49也应该不错。也就是说存在某种关系,而不是像离散动作那种one-hot,动作之间没有任何联系。所以在拟合动作概率的时候先把logits过了sigmoid函数,然后计算一个新的logits,最后再算softmax。解释如下

这个式子想说的就是,我要想选i这个动作,那i前面的动作的logits都要大才行,后面的动作的logits要小。这种方式的动机在于连续空间的动作是存在大小关系的而不是独立的,所以离散化后的动作空间也应该保留这种顺序关系。
总结:直觉上有点道理,但是这种做法怎么就反应动作的顺序了,不知道原理是啥。而且从文章看,K具体怎么选也不好调。
疑问:不知道为啥这个假设work,感觉不是所有的动作空间都有这个性质吧,还是说因为这个是连续空间离散化而来的,就有这种顺序关系?


 浙公网安备 33010602011771号
浙公网安备 33010602011771号