Finite-time Analysis of the Multiarmed Bandit Problem

发表时间:2002(Machine Learning, 47, 235–256, 2002)
文章要点:这篇文章主要是分析了针对Multiarmed Bandit Problem的几个经典算法的收敛性。我们知道这类问题主要就是在解决exploration versus exploitation dilemma,他的regret至少是以动作次数的对数增长的,但是这个结论只是渐进性的,不够具体。作者就分析了四个具体算法的finite-time下的性质。
分析的第一个算法是经典的UCB1,这个算法动作的选择策略如上图,以\(\bar{x}_j+\sqrt{\frac{2\ln n}{n_j}}\)选择动作,其中\(\bar{x}_j\)是当前得到的arm \(j\)的平均reward,\(\sqrt{\frac{2\ln n}{n_j}}\)是一个和访问次数有关的项,用来控制exploration。得到的结论就是

这里

这个定理告诉了我们,对于做了n次动作后,当前的regret被bound在什么范围,这个结论可比渐进性强多了。
第二个算法是UCB2

之前UCB1里面有个\(8/\Delta^2_i\),UCB2可以把这个数缩小到任意接近\(1/2\Delta^2_i\)。UCB2算法的流程是这样的,他控制exploration的项变成了
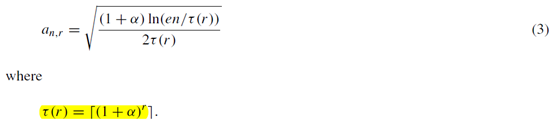
并且选定一个动作后,要执行\(\tau (r_j+1)-\tau (r_j)\)次,而不是一次。这里有个常数\(\alpha\)需要设置。得出的结论是

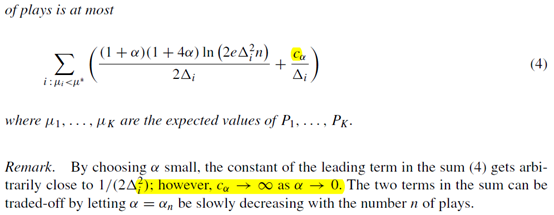
也是直接就告诉了我们regret的bound在哪。
第三个算法是\(\epsilon_n\)-greedy。我们知道如果是\(\epsilon\)-greedy的话,因为\(\epsilon\)永远不衰减,这个regret的增长速度是线性的,而如果我们用如下的方式来衰减的话,就可以控制在对数速度。

这里K就是K个arm,d和c是参数。得出的结论是


最后一个算法是UCB1-NORMAL,就是对arm的reward 做了一个正态分布的假设,选择动作的规则有部分变化

得出的结论是
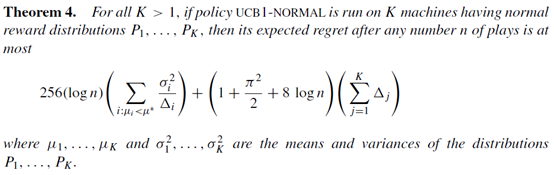
总结:一篇很经典的对Multiarmed Bandit Problem做理论分析的文章,最开始发在ICML 1998,后面发在期刊Machine Learning,感觉可以从这篇开始入门一点理论分析了。证明在原论文里面写的很好,这里就不贴了。
疑问:其实不太懂这个bound到底算不算紧,但是这个结论肯定是非常牛皮的了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号