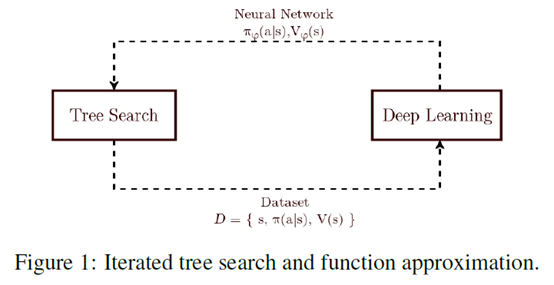
A0C: Alpha Zero in Continuous Action Space

发表时间：2018
文章要点：这篇文章提出A0C算法，把AlphaZero做到连续动作空间上，主要使用的方式是progressive widening和continuous prior（就是continuous policy network）。具体的，progressive widening就是说在做MCTS的时候，节点的扩展没法像离散动作空间那样直接把所有动作都扩展开，所以扩展的节点是一个和当前模拟次数有关的一个函数

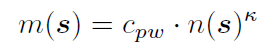
这里\(n(s)\)就是当前状态访问次数，\(κ\)和\(n\)是参数，\(m(s)\)就是在这个状态下扩展多少个节点。这个意思就是说，随着访问次数增加，扩展节点的个数才会逐渐增加，这个就是progressive的含义。
另一个改变就是Continuous policy network prior。在做MCTS的时候需要给每个节点一个先验概率，之前离散的情形下，网络是输入状态然后给出所有动作的概率。连续的情形显然办不到，于是变成输入状态和一个动作，给出概率。训练的时候，就根据当前树的节点以及孩子节点的访问次数，算一个归一化的概率

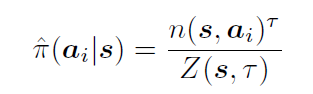
严格意义上来说，离散情形应该定义概率密度函数，并且满足积分是1.但是作者也说了，这个其实是很难做到，所以实际操作的时候还是通过这种用访问次数来估计一个概率的方式来做的。最后为了避免policy collapse，训练的时候还加了个entropy的正则项。
这里还有一个细节可以注意一下，就是在做progressive widening的时候，扩展节点的动作选择，也刚好可以用这个policy来采样概率大的动作来扩展。
其他地方就和AlphaZero一样了，比如MCTS的流程，value的估计等等。
总结：章很简洁，方法也make sense。之前我也在考虑怎么把MCTS做到连续动作空间，结果这么久了也一直没做过，唉。
疑问：里面前面对policy的分布要求那里，理论上要求概率密度函数的积分是1，但是实际上做不到。于是作者又转成了离散的方式，用visit count算概率。话说能不能做个高斯假设之类的，用这种方式来做行得通吗？
这个文章式子（6）那里明明是最小化KL divergence，为啥会用REINFORCE算法来优化这个loss？

文章估计value的时候，说直接用网络在根节点输出value，难道不结合树搜索先往下走一定深度吗？