初级模拟电路:4-3 BJT晶体管的交流建模
1. 四种BJT模型概述
对BJT晶体管建模的基本思路就是,用电路原理中的五大基本元件(电阻、电容、电感、电源、受控源)构建一个电路,使其在一定工作条件下能等效非线性半导体器件的实际工作。一旦确定了交流等效电路,电路中的BJT就可以用这个等效电路来替代,然后用基本的电路计算方程,就可以大致计算出电路中需要确定的电压、电流等物理量。
在一般的模电教材中,常会提到以下4种BJT晶体管的模型:混合π模型、re模型、混合等效模型、简化混合等效模型。这么多模型一起拿出来,很容易把人搞晕。其实,所谓一图胜千言,只要画张图你就明白它们之间的关系了,而且基本上一辈子也忘不了。4种模型的关系如下图所示:
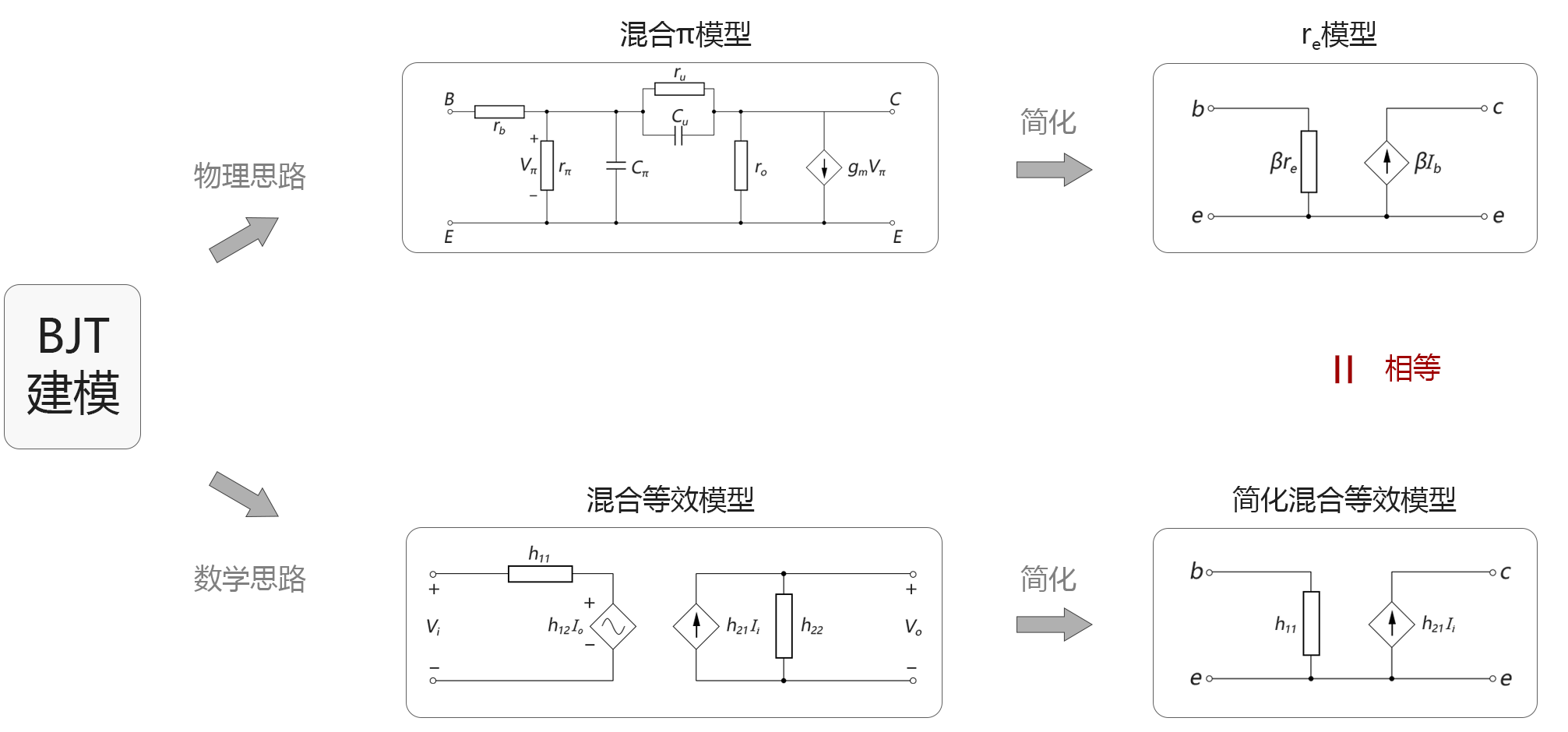
图4-3.01
从物理思路出发,可以得到“混合π模型”,对其进行简化,就是“re模型”。
从数学思路出发,可以得到标准的“混合等效模型”,对其进行简化,就是“简化混合等效模型”。而且,用两种方式最终得到的简化模型是一致的。
下面我们分别对其进行简单说明:
(1)混合π模型
首先从物理思路出发,要对BJT建模:最好能彻底搞清楚其内部的结构和工作机理,这样就能绘制出一个精确的等效电路。经过固体物理科学家和材料科学家多年的不懈努力,人们终于得到了一个比较精确的BJT晶体管内部的等效电路图,如下图所示:
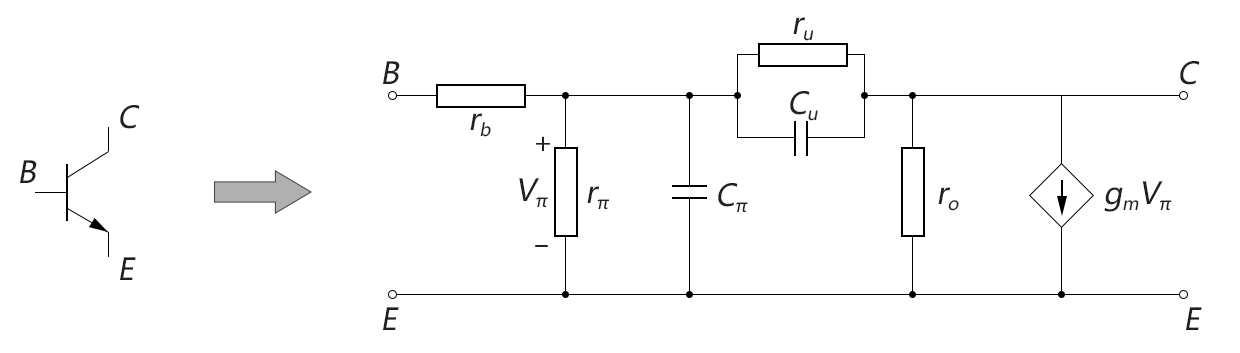
图4-3.02
由于电路的形状有点像希腊字母的“π”样子,故称为混合π模型(hybrid π model)。混合π模型一般专门用于高频分析,其优点是对BJT的等效比较精确;缺点是计算比较复杂,这种带电容和受控源的π型电路,如果不用仿真软件,纯用手算是非常麻烦的。
(2)re模型
后来人们发现,在中低频和一些要求不高的场合下,其实不用画这么复杂的π型电路,可以用更简单的电路来作近似,这个就是're模型'(re model),如下图所示:
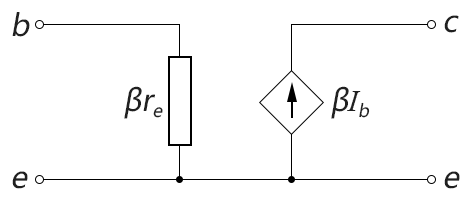
图4-3.03
re模型的优点是计算简单,适合用手算来对BJT电路进行大致的交流分析(至于为什么要叫“re模型”,等下一小节我们详细分析完re模型你就明白了)。这个也是目前普遍使用的BJT分析模型,我们本章后面的交流分析基本都是基于re模型的。但由于re模型中没有电容,所以无法用于高频分析。
(3)混合等效模型
另一种建模思路是数学思路:就是我不管你BJT内部如何工作,我只当你是个二端口黑箱,只要我在两个端口测出各个条件下的电压电流,就可以对你建模。
在电路原理的二端口理论中,有6种可用于二端口分析的参数模型(分别是:z参数、y参数、h参数、g参数、T参数、t参数),对BJT的分析建模,业内普遍采用的是h参数模型,h参数的全称是混合参数(hibrid parameter),h参数二端口模型和方程如下图所示:
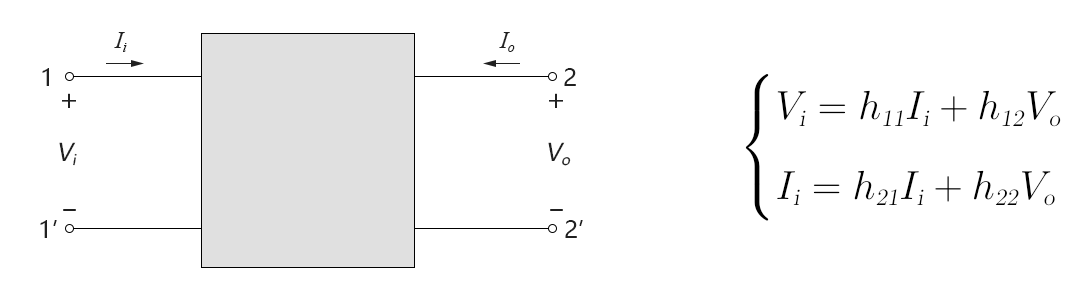
图4-3.04
对以上方程画出二端口内部的标准数学等效电路,就是下面这个样子:
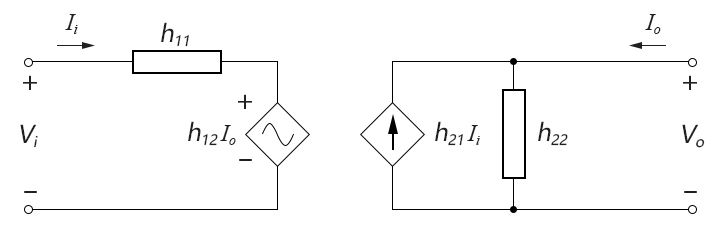
图4-3.05
因为这个等效电路来源于“混合参数二端口模型”,故称为“混合等效模型”。这里你可以先不深究,后面我们还要花一个小节专门讲解如何分析混合等效模型。
由于早期人们对半导体内部的工作机理还不是非常了解,故当时人们对半导体的性能描述用的都是这种黑箱描述的“混合等效模型”,各大半导体制造商在数据规格书中用的也都是混合等效模型参数(这就是为啥你经常在BJT数据规格书中看到诸如hfe, hie之类的参数的原因)。虽然后来更精确的“混合π模型”被发表出来,但由于各厂商已经习惯了用h参数来描述BJT性能,也就约定俗成一直用到今天了。
(4)简化混合等效模型
上面的混合等效参数模型一共有4个h参数,计算起来还是有点复杂。在一些要求不高的场合,可以对其进行进一步简化。对于BJT晶体管,人们在实测中发现:h12通常参数比较小,故可近似视为短路;而h22参数通常比较大,故可近似视为开路。简化后的电路如下图所示:

图4-3.06
这样一简化后,就只剩2个h参数了,计算量大大减少。而且这个“简化混合等效模型”同前面的“re模型”居然是一样的,真可谓是殊途同归。
2. BJT的外围交流等效电路
外围电路的交流等效电路比较简单,核心就是电路原理中交流等效分析的两个原则:
● 所有电容都视为交流短路。
● 所有直流电压源都视为交流短路,直流电流源视为交流开路。
这两个原则应用到BJT的外围交流电路中,我们以下面一个具体的例子来说明:
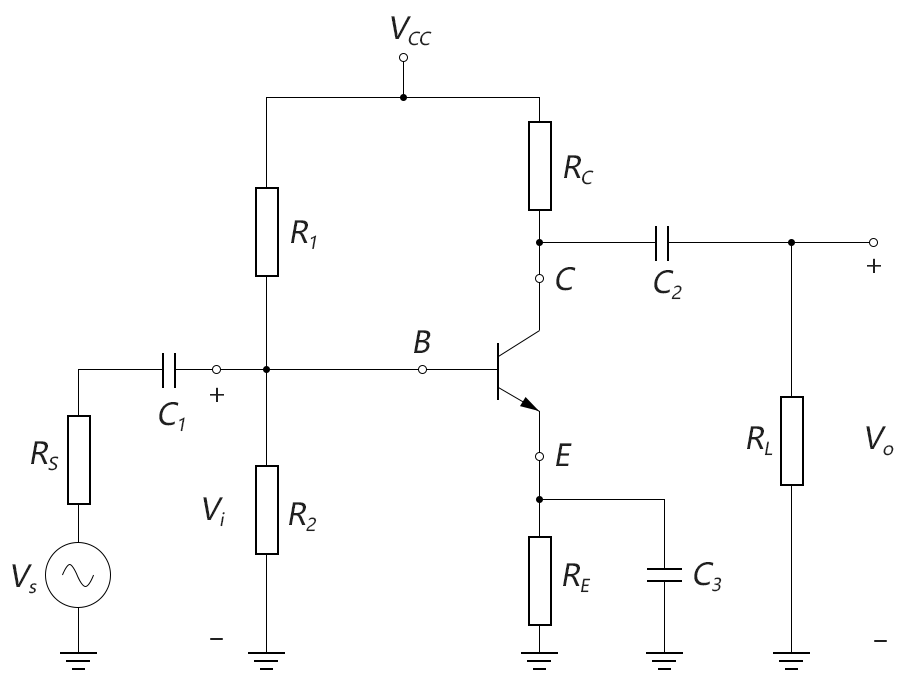
图4-3.07
上图是一个典型的分压偏置的共射放大电路,我们对其应用上面的2个原则画出交流等效电路,如下图所示:
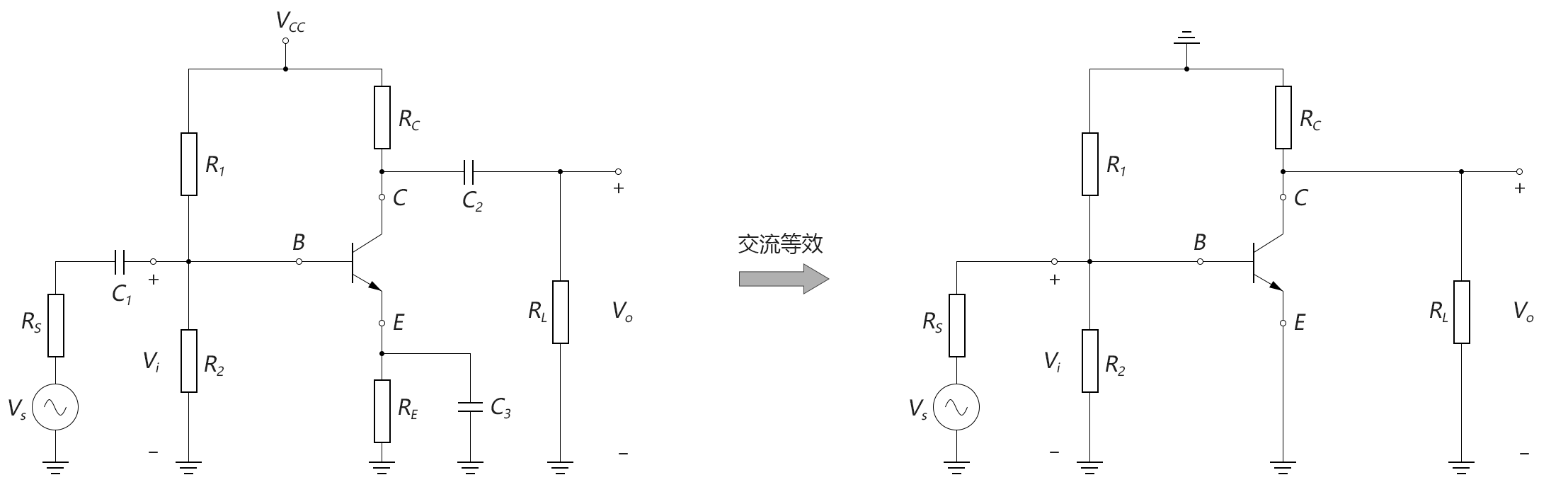
图4-3.08
对上图进一步进行整理,可以得到如下图所示的更加简洁的交流等效电路:
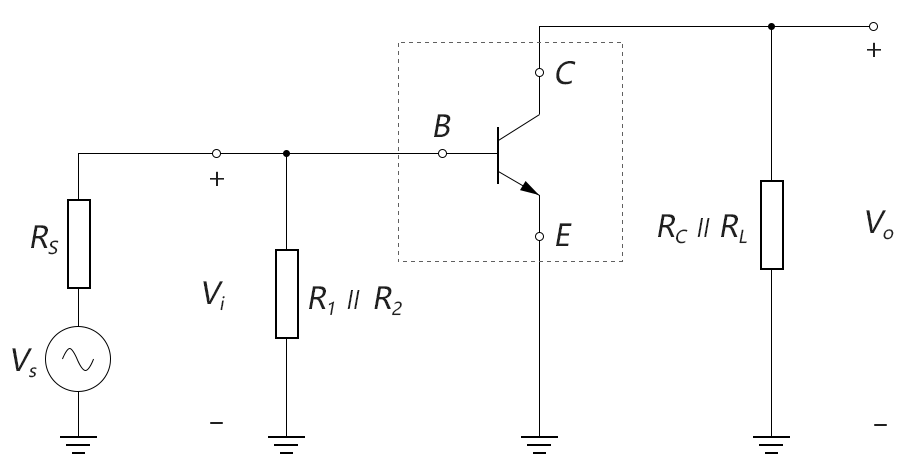
图4-3.09
然后将前面的BJT等效电路模型替换上图中的BJT元件,就可以对电路进行交流分析了。
3. 阻抗与导纳
阻抗与导纳是电路交流分析中的常用概念,一般的电路原理书都讲得很清楚了。这里我再简单阐述一下,作为进入交流分析前最后的铺垫知识。
在直流电路中,电容视为开路,电感视为短路,因此只有“电阻”,根本不需要“阻抗”的概念。只要一个实数的阻值,就足以描述“电压-电流”关系。
而在正弦交流电路中,常常会包含电容和电感,只要涉及到电容电感,仅用一个实数电阻值是无法完全描述电路中“交流电压-交流电流”关系的,此时需要用一个复数值来描述“交流电压-交流电流”关系,这个复数值就称为:阻抗(impedence),如下图所示:

图4-3.10
其中,阻抗Z的实部R为“电阻”;阻抗Z的虚部X为“电抗”,用来描述电容和电感对交流信号相位的影响。阻抗、电阻、电抗的单位都为:欧姆(Ω)。
电抗X可正可负。如果X为正值,那么这个阻抗整体称为:感性阻抗;如果X为负值,那么可以整体称为:容性阻抗。如果电抗X为0,即电路中没有电容和电感(或电容电感相互抵消),那么“电阻”和“阻抗”是同一个意思。在我们在上一小节中的分析中,由于电路中没有电容和电感,为阐释概念方便,我们基本都用的是“输入电阻”和“输出电阻”这样的称呼。
而一般人们对于交流电路,习惯用“阻抗”这个名词。所以从下一小节起,不管电路中有没有电容和电感,我们都会用“输入阻抗”和“输出阻抗”这样的名词来表示“输入电阻”和”输出电阻”。
至于“导纳”的含义也是类似,如下图所示:

图4-3.11
导纳、电导、电纳的单位都为:西门子(S)。导纳与阻抗互成倒数关系:
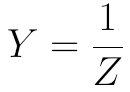
( end of 4-3)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号