CNN卷积神经网络

CNN网络结构

在神经网络的发展历史中介绍了，CNN被广泛应用与图像领域，本文对CNN网络结构与算法进行进一步的介绍。

基本网络结构

CNN的网络结构一般包括：

• 输入层
• 由若干卷积层、激活函数、池化层、全连接层组成的隐藏层
• 使用softmax激活函数的输出层

卷积运算

CNN中的卷积运行表示为：

\[S(i,j) = (X*W)(i,j) = \sum_m\sum_nX(i+m)(j+n)W(m,n) \]

其中，X表示输入，W表示卷积核

卷积层

CNN的卷积运算其实就是对输入的局部矩阵和卷积核的矩阵各个位置上的元素相乘再相加。
例如下图，输入为一个3×4的矩阵，卷积核为2×2的矩阵，卷积每次移动的步长为1。首先对输入矩阵左上角的2×2的矩阵与卷积核矩阵进行按位置相乘相加的运算，即得到卷积后第一个元素的值：aw+bx+ey+fz。接着对卷积核向右移动一个位置，对第二个局部矩阵(b,c,f,g)与卷积核进行卷积运算，得到结果: bw+cx+fy+gz，以此类推，最终得到的卷积层输出为一个2×3的矩阵。

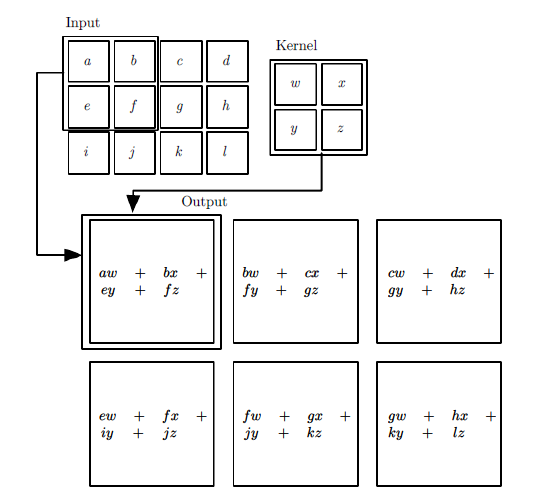
对卷积层的输出，一般会通过ReLU激活函数（\(Relu(x) = max(0,x)\)），将输出张量中小于0的元素值都变为0。

卷积层参数说明

pytorch对Conv2d的定义如下：

def __init__(self,
             in_channels: int,
             out_channels: int,
             kernel_size: Tuple[int, ...],
             stride: Tuple[int, ...] = 1,
             padding: str = 0,
             dilation: Tuple[int, ...] = 1,
             groups: int = 1,
             bias: bool = True,
             padding_mode: str = 'zeros',
             device: Any = None,
             dtype: Any = None) -> None

其中，in_channels表示输入通道个数，对于原始图片来讲，彩色图片是RGB为3，黑白图片为1；对于中间的卷积层来讲，in_channels为上一次卷积的out_channels
out_channels为卷积操作后的输出，取决与卷积核的个数，如上所述，也会是下一个卷积层的in_channels
stride表示卷积运算时的步进

例如：输入时一个32×32×3的图片，3表示RGB，每个卷积核是5×5×3，每个卷积核运算后将产生一个feature map（大小为28×28），有6个卷积核就产生6个feature map（28×28×6）

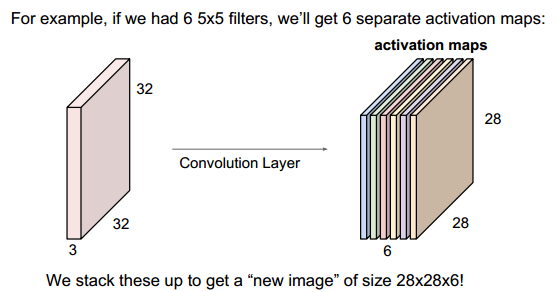
对于W×H×D的图片，使用F×F的卷积核运算后，得到的输出矩阵的参数计算如下：

Width = (W - F + 2P)/S +1
Height = (H- F + 2P)/S +1
Depth = D

其中P表示填充长度，S表示步进stride

pytorch卷积层参数示例

首先定义卷积层：

conv_layer = torch.nn.Conv2d(
    in_channels=3,
    out_channels=10,
    kernel_size=5
)

打印出conv的weight：

conv_layer.weight.shape

可以看到shape为[out_channels, in_channels, kernel_height, kernel_width]的矩阵，矩阵的内容在训练时拟合得到:

torch.Size([10, 3, 5, 5])

打印出conv的bias：

conv_layer.bias.shape

结果为：

torch.Size([10])

模型推理时，卷积层就是使用卷积核的weight和bias参数与输入进行计算

池化层

池化层的作用是对输入张量的各个子矩阵进行压缩，例如2×2的池化，就是将子矩阵的每2×2个元素变成一个元素，3×3的池化就是将子矩阵的每3×3个元素变成一个元素。
对输入子矩阵的n×n个元素变成一个，一般有两个方法：一个是Max，即取所有元素的最大值。另一个是Average，即取所有元素的平均值。

下图示例：按照最大池化方法，采用2×2的池化，步进为2.
首先对红色2x2区域进行池化，由于此2x2区域的最大值为6.那么对应的池化输出位置的值为6，由于步幅为2，此时移动到绿色的位置去进行池化，输出的最大值为8.同样的方法，可以得到黄色区域和蓝色区域的输出值。最终，我们的输入4x4的矩阵在池化后变成了2x2的矩阵。进行了压缩。

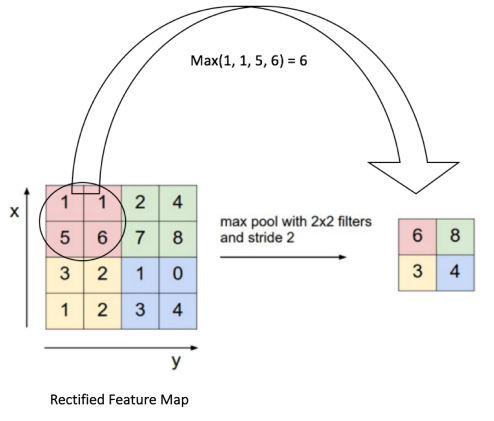
池化过程就是局部取最大值、平均值等，因此没有weight和bias

全连接层

全连接层的每一个节点都与上一层的所有节点相连，全连接层通过本层的w * x + b运算，实现从一个特征空间到另一个特征空间的线性变换，例如CNN中使用FC作为分类器，把卷积、池化处理后的特征空间映射到样本标记空间

CNN前向传播算法

输入层到卷积层的前向传播

输入层是第一层，一般输入层连接的第二层都是卷积层。输入层到卷积层的前向传播的表达式：

\[a^2 = \sigma(z^2) = \sigma(a^1 * W^2 + b^2) \]

其中：上标代表层数，星号代表卷积，b代表偏移向量，\(\sigma\)代表激活函数，一般为ReLU

隐藏层到卷积层的前向传播

类似的，卷积层处于网络结构中间位置的情况下，隐藏层向卷积层的前向传播算法可以表示为：

\[a^l = \sigma(z^l) = \sigma(a^{l-1} * W^l + b^l) \]

隐藏层到池化层的前向传播

池化层的目的是对输入进行压缩，例如输入矩阵是N×N维的，池化大小是K×K的区域，则输出的矩阵是\(\frac{N}{K} * \frac{N}{K}\)维。

隐藏层到池化层前向传播涉及的参数包括：

• 池化区域的大小K
• 池化标准，一般是Average、Max

隐藏层到全连接层的前向传播

全连接层与DNN模型相同，前向传播算法为：

\[a^l = \sigma(z^l) = \sigma(W^la^{l-1}) + b^l \]

这里的激活函数\(\sigma\)一般为sigmoid或tanh。

隐藏层到全连接层前向传播涉及的参数包括：

• 全连接层的激活函数，如sigmoid、tanh
• 全连接层的神经元个数

经过若干全连接层之后，最后一层为softmax输出层，输出层和普通全连接层的唯一区别是使用softmax函数。

CNN前向传播算法小结

输入

• 输入数据，如图片样本
• CNN模型的层数
• 所有隐藏层的类型
• 对于卷积层，涉及卷积核的大小K，卷积核子矩阵的维度F，填充大小P，步进S
• 对于池化层，涉及池化区域大小，池化标准（如Max、Average等）
• 对于全连接层，涉及全连接层的激活函数（输出层除外），各层的审计格式

输出

CNN的模型输出\(a^L\)

前向传播算法

1、根据输出层的填充大小P，填充原始图片的边缘，得到输入张量\(a^1\)
2、初始化所有隐藏层的参数W、b
3、for \(l\)=2 to \(L-1\):
a) 如果第\(l\)层为卷积层，则输出为：

\[a^l = ReLU(z^l) = ReLU(a^{l-1} * W^l + b^l) \]

b) 如果第\(l\)层是池化层，则输出为：

\[a^l = pool(a^{l-1}) \]

其中pool指按照池化区域大小k和池化标准将输入张量缩小的过程

c) 如果第\(l\)层是全连接层，则输出为：

\[a^l = \sigma(z^l) = \sigma(W^la^{l-1}) + b^l \]

4、对于输出层（第L层）：

\[a^L = softmax(z^L) = softmax(W^La^{L-1} + b^L) \]

参考

刘建平博客：https://www.cnblogs.com/pinard/p/6483207.html
https://towardsdatascience.com/pytorch-conv2d-weights-explained-ff7f68f652eb
https://www.cnblogs.com/hejunlin1992/p/7624807.html
https://www.cnblogs.com/gezhuangzhuang/p/10917249.html
https://www.cxyzjd.com/article/weixin_40904071/90636096