深度神经网络DNN介绍
DNN网络结构
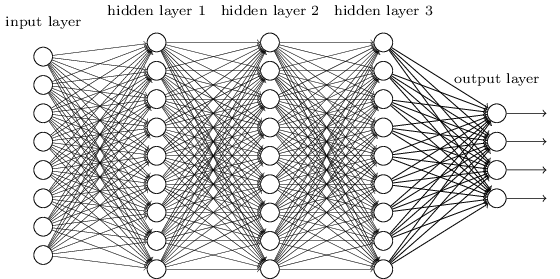
DNN是从多层感知器发展而来的第三代神经网络，DNN的网络结构分为三部分：输入层、隐藏层、输出层。
DNN的层与层之间是全连接的，第\(i\)层的任意一个神经元一定与第\(i+1\)层的任意一个神经元连接.
从小的局部模型来讲，DNN和感知器一样，包括：
- 线性关系：\(z=\sum_1^m{w_i}{x_i}+b\)
- 激活函数：\(\sigma(z)\)
DNN的前向传播算法
符号表示
-
第\(l-1\)层有\(m\)个神经元，第\(l\)层有\(n\)个神经元
-
第\(l\)层的权重系数矩阵\(W^l\)：\(n*m\)的矩阵
-
第\(l\)层的偏移向量\(b^l\)：\(n*1\)的向量
-
第\(l-1\)层的输出\(a^{l-1}\)：\(m*1\)的向量
-
第\(l\)层未激活前的线性输出\(z^l\)：\(n*1\)的向量
-
第\(l\)层的输出\(a^l\)：\(n*1\)的向量
输入
- 总层数\(L\)
- 所有隐藏层和输出层对应的权重系数矩阵\(W^i\)，偏移向量\(b^i\)
- 输入向量\(x\)
输出
输出层的结果\(a^L\)
前向传播算法
1）初始化\(a^1 = x\)
2) for \(l=2\) to \(L\)，计算：
每一层向前计算，最终的结果即为\(a^L\)
DNN的反向传播算法
反向传播算法的用途
在监督学习算法中，假设有\(m\)个训练样本：\({(x_1,y_1),(x_2,y_2),...,(x_m,y_m)}\)，其中\(x\)为输入向量，特征维度为\(n_in\)，\(y\)为输出向量，特征维度为\(n_out\)，我们需要用这\(m\)个训练样本训练出一个模型，用于预测未知样本的输出结果。
DNN反向传播算法用于模型训练时求得最佳的权重系数矩阵\(W\)和偏移向量\(b\)。与传统机器学习类似，使用一个合适的损失函数来度量训练样本的输出结果损失，然后对这个损失函数进行优化求最小极值，最终得到的一系列线性系数矩阵\(W\)和偏移向量\(b\)即为最终结果。
对DNN的损失函数使用梯度下降法进行迭代优化求极小值的过程即为反向传播算法。
输入
- 网络结构总层数\(L\)
- 隐藏层与输出层的神经元个数
- 激活函数
- 损失函数
可以选择不同的损失函数，例如使用均方误差来度量损失，对于每个样本，期望最小化：
- 迭代步长\(\alpha\)
- 最大迭代次数\(MAX\)
- 停止迭代阈值\(\varepsilon\)
- \(m\)个训练样本：\({(x_1,y_1),(x_2,y_2),...,(x_m,y_m)}\)
输出
各隐藏层与输出层的线性关系系数矩阵\(W\)和偏移向量\(b\)
反向传播算法
1、初始化各隐藏层与输出层的线性关系系数矩阵\(W\)和偏倚向量\(b\)的值为一个随机值。
2、for iter from 1 to MAX:
2.1 for \(i=1\) to \(m\):
a) 将DNN输入\(a^1\)设置为\(x_i\)
b) for \(l=2\) to \(L\), 进行前向传播算法计算\(a^{i,l} = \sigma(z^{i,l}) = \sigma(W^la^{i,l-1}+b^l)\)
c) 通过损失函数计算输出层的\(\delta^{i,L}\)
d) for \(l=L-1\) to 2, 进行反向传播算法计算: \(\delta^{i,l} = (W^{l+1})^T\sigma^{i,l+1}\Theta\sigma'(z^{i,l})\)。其中，\(\Theta\)表示Hadamard积，对于两个维度相同的向量\(A(a_1,a_2,...a_n)^T\)和\(B(b_1,b_2,...b_n)^T\)，则\(A\Theta B = (a_1b_1,a_2b_2,...a_nb_n)^T\)
2.2 for \(l=2\) to \(L\), 更新第\(l\)层的\(W^l, b^l\):
2.3 如果所有\(W\)、\(b\)的变化值都小于迭代停止阈值\(\varepsilon\)，则跳出循环到步骤3
3、输出各隐藏层和输出层的线性关系系数矩阵\(W\)和偏移向量\(b\)
