一文入门现代密码学

主页

微信公众号：密码应用技术实战
博客园首页：https://www.cnblogs.com/informatics/
GIT地址：https://github.com/warm3snow

本文组织

  • 简介：介绍密码技术产生背景、重要性、以及发展阶段
  • 现代密码体系
  • 数字证书
  • 数字信封
  • 密钥协商
  • TLS/SSL通信
  • 常见实现和推荐
  • 总结
  • 参考资料

简介

密码技术产生的背景

密码技术最早应用于军事，并随着社会和信息技术的发展不断演变。

密码技术的发展背景:

  • 军事和外交：密码技术的起源可以追溯到古代，最早的密码用于军事和外交通信，以保护敏感信息不被敌方获取。例如，古希腊的斯巴达使用简单的替换密码，而凯撒密码则是古罗马的一种著名加密方法。
  • 商业秘密：随着商业活动的增加，商人们也开始使用密码来保护交易信息和商业秘密。
  • 计算机和网络的兴起：20世纪中叶，计算机技术的快速发展和互联网的普及使得信息的传输和存储变得更加便捷，但同时也带来了信息安全的挑战。黑客攻击、数据泄露等问题日益严重，促使密码技术的发展。
  • 数字化转型：进入21世纪，信息化和数字化的浪潮席卷各个行业，个人和组织在日常生活和工作中产生大量敏感数据，保护这些数据的安全成为迫切需求。

密码技术在信息安全中的重要性

信息安全是指保护信息的机密性、完整性和可用性，以防止未授权访问、使用、披露、破坏或修改。信息安全的目标是确保信息在存储、处理和传输过程中的安全性，防止信息泄露、丢失或被篡改。
信息安全的基本要素包括几个重要的属性：

  • 机密性（Confidentiality）：机密性是指保护信息不被未授权的用户访问或泄露的能力，机密性确保只有被授权的用户或系统能够访问特定的信息。这通常通过加密、访问控制和身份验证等手段来实现。机密性的重要性在于保护敏感数据（如个人信息、财务数据和商业机密）不被泄露或滥用。
  • 完整性（Integrity）：完整性是指确保信息在存储、传输和处理过程中保持准确和一致的能力。完整性确保数据未被未授权的用户篡改或损坏。这可以通过使用哈希函数、数字签名和校验和等技术来验证数据的完整性。完整性的重要性在于确保信息的真实性和可靠性，防止数据被恶意修改或损坏。
  • 可用性（Availability）：可用性是指确保信息和系统在需要时能够被授权用户访问的能力。可用性确保系统和数据在任何时候都能正常运行，用户可以随时访问所需的信息。这通常涉及到系统的冗余设计、备份和恢复策略，以及防止拒绝服务攻击（DoS）等措施。可用性的重要性在于确保业务连续性和用户满意度。
  • 不可否认性（Non-repudiation）：不可否认性是指确保发送方或接收方无法否认其参与某个通信或交易的能力。：不可否认性通常通过数字签名和审计日志等技术来实现。它确保交易的双方都无法否认其行为，从而提供法律和合规性支持。这在电子商务和法律文件中尤为重要，确保交易的真实性和责任。
  • 可控性（Controllability）：可控性是指对信息和系统的访问和使用进行有效管理和控制的能力。可控性确保组织能够监控和管理对信息的访问权限，确保只有授权用户能够访问和操作特定的信息。这通常涉及到访问控制策略、用户身份验证和权限管理等措施。可控性的重要性在于防止内部和外部的安全威胁，确保信息的安全性和合规性。

其中前三者在信息安全等级保护中通常被称为信息安全三要素CIA（英文首字母简称）。随着计算机和信息技术的发展，信息安全越来越受到重视，国内相继颁布了类似《个人数据保护法》、《网络安全法》等相关法律条例。密码技术作为信息安全的核心技术手段，目前已非常成熟。

古典密码vs现代密码

密码技术的发展可以分为两个阶段，第一个阶段是公元前几世纪至20世纪初的古典密码，第二个阶段是20世纪中叶至今的现代密码

对比 古典密码 现代密码
定义 古典密码是指在计算机技术普及之前使用的传统加密方法，
通常基于简单的替换或置换技术。		 现代密码是指在计算机和网络技术发展后，
采用复杂算法和数学理论进行加密的技术。
举例 凯撒密码、维吉尼亚密码、替换密码等 AES（高级加密标准）、RSA、ECC等
加密方法 主要使用替换和置换技术 使用复杂的数学算法和密钥管理
密钥管理 通常手动管理，密钥长度较短 采用自动化密钥管理，密钥长度较长
安全性 安全性较低，易受频率分析等攻击 安全性高，抵御多种攻击方式
适用场景 适用于简单的通信和信息保护 适用于复杂的网络通信和数据保护
实现复杂度 实现相对简单 实现较为复杂，需要专业知识
计算需求 计算需求低 计算需求高，通常需要专用硬件支持

由于古典密码与现代密码相比，在密码技术构造上比较简单且仅包含加解密技术，我们这里不做过多介绍，感兴趣的可以搜索维基百科古典密码。后文我们主要针对现代密码进行介绍。

现代密码

现代密码（Modern Cryptography）是指在计算机科学和信息技术发展背景下，采用复杂的数学算法和理论来实现数据加密、身份验证、数据完整性和不可否认性等安全功能的技术。现代密码学不仅关注数据的机密性，还涉及多个方面的安全性，广泛应用于网络通信、电子商务、数据存储等领域。

现代密码技术体系：

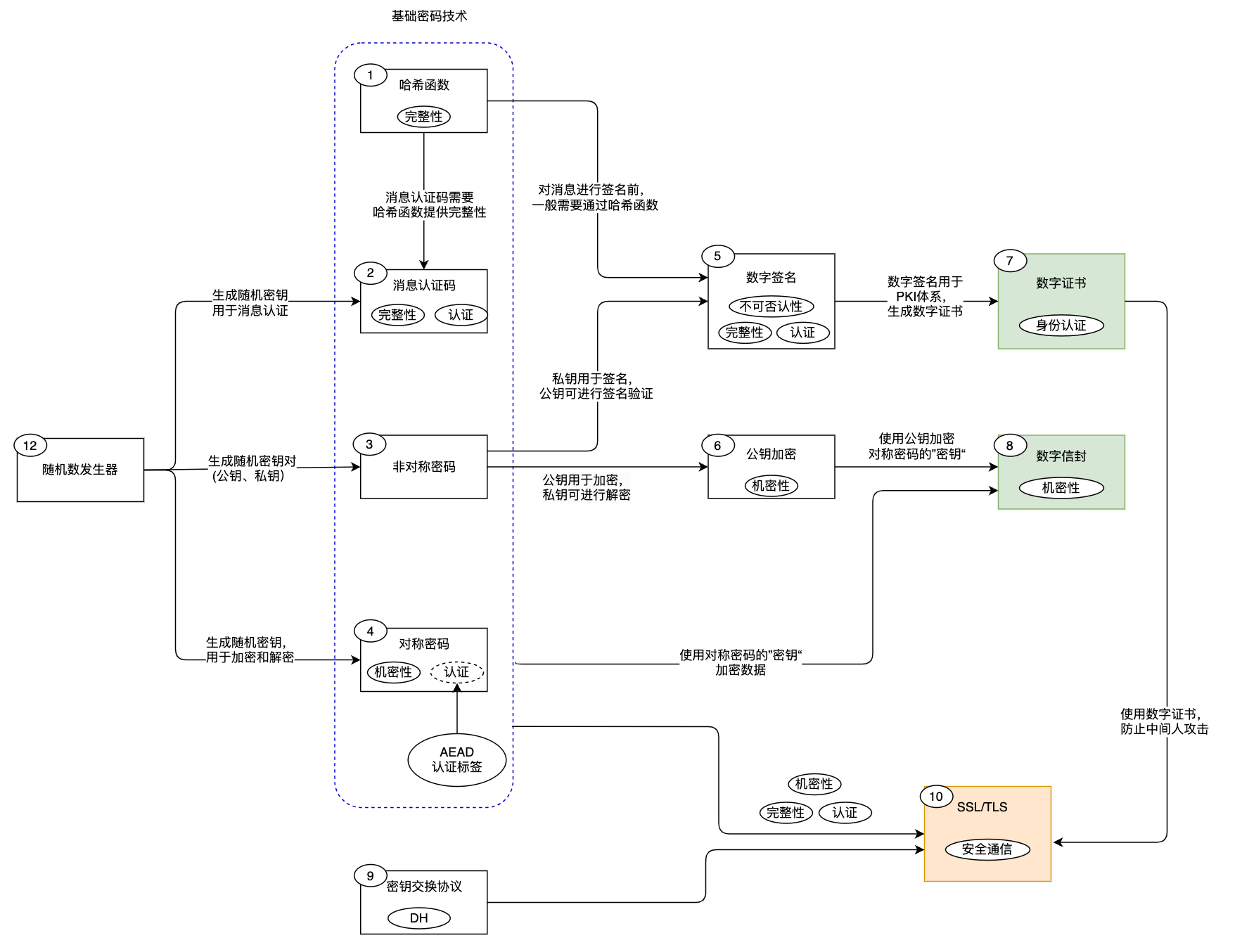
image

  • 现代密码包含4大基础密码技术：对称密码、非对称密码、哈希函数和消息认证码。
  • 哈希函数和消息认证码通常用于实现数据完整性，其中消息认证码还可以用于实现数据认证。
  • 对称加密和非对称加密用于实现数据的保密性，非对称加密还可以用于实现数字签名。
  • 基础密码技术可以组合使用，构建更复杂的密码协议和安全机制，如数字证书、数字信封、SSL/TLS等。

哈希函数

哈希函数（Hash Function）是一种将任意长度的输入数据映射为固定长度输出的函数，通常用于实现数据的完整性验证和数据摘要。哈希函数有多个名称，如散列函数、摘要函数等

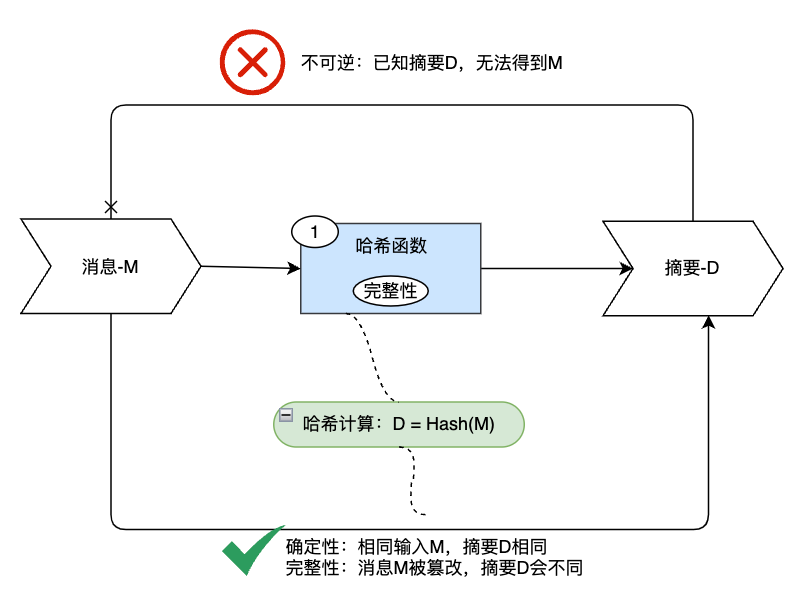
image

哈希函数的特点是：

  • 哈希函数的输出长度固定，通常为128位、256位、512位等。
  • 哈希函数是单向函数，不可逆，无法从哈希值反推原始数据。
  • 哈希函数碰撞概率极低，即不同的输入数据产生相同的哈希值的概率极小，碰撞概率可忽略不计。
  • 哈希函数的计算速度快，适合大规模数据处理。
  • 常见的哈希函数有MD5、SHA-1、SHA-256、SHA-3、国密SM3等。
  • 哈希函数常用于密码学中的数据完整性验证、数字签名、消息认证码等。

哈希函数构造：

\[D = Hash(M) \]

其中：\(M\)为消息，\(D\)为哈希值/摘要值，\(Hash\)为哈希算法

哈希函数使用流程：

  • 发送者使用哈希函数计算消息\(M\)的摘要\(D\)，并将\((M, D)\)发送给接受者
  • 接受者使用哈希函数重新计算消息\(M\)的摘要\(D'\), 并比较\(D' \stackrel{?}{=} D\), 如果相等则表示消息\(M\)是完整的。

注：哈希函数一般不单独使用，通常会结合数字签名技术，防止攻击者同时修改\((M,D)\)，造成消息被篡改，但是验证仍然通过。

消息认证码

消息认证码（Message Authentication Code, MAC， 又称为HMAC）是一种用于验证消息完整性和真实性的密码技术，通常由一个密钥和消息组成，生成固定长度的认证码。消息认证码常用于验证数据的完整性和真实性，防止数据被篡改或伪造。

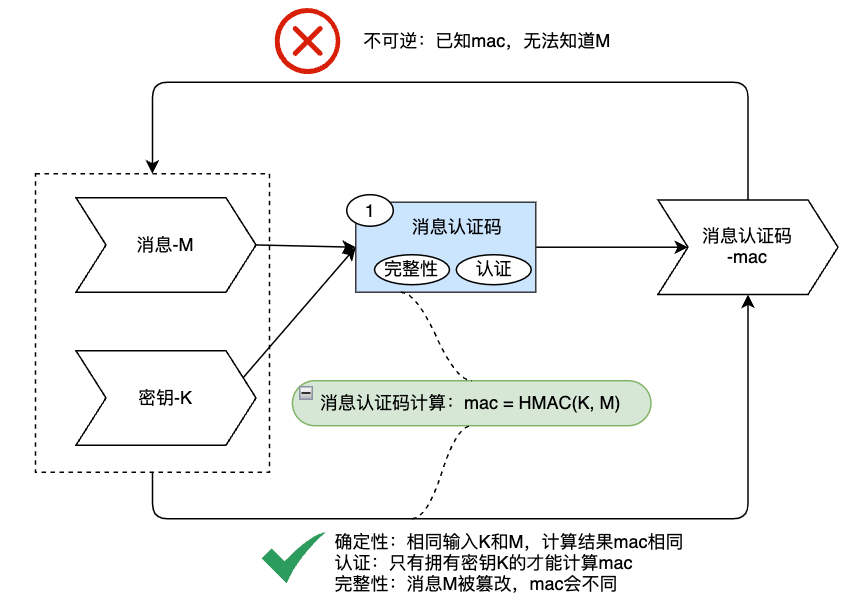
image

消息认证码的特点是：

  • 消息认证码使用密钥对消息进行加密，生成固定长度的认证码，发送者和接收者需要共享密钥。
  • 消息认证码是单向函数，不可逆，无法从认证码反推原始消息。
  • 消息认证码碰撞概率极低，即不同的消息产生相同的认证码的概率极小，碰撞概率可忽略不计。
  • 消息认证码计算速度快，适合大规模数据处理。
  • 消息认证码可以验证消息的完整性和真实性，防止数据被篡改或伪造。
  • 常见的消息认证码算法有HMAC-MD5、HMAC-SHA1、HMAC-SHA256、HMAC-SHA3、HMAC-SM3等
  • 消息认证码常用于数据认证、数据完整性验证等场景。

消息认证码构造：

\[mac = HMAC(K, M) \]

其中，\(K\)为密钥(不公开), \(M\)为消息，\(HMAC\)为消息认证码算法

消息认证码使用流程：

  • 共享密钥\(K\)：首先发送者和接受者要共享密钥\(K\)，可以通过密钥协商协议生成、也可以由一方生成并安全传输给另一方。
  • 发送者计算消息\(M\)的认证码\(mac\)，并将\((M, mac)\)发送给接受者。
  • 接受者使用重新计算消息\(M\)的消息认证码\(mac'\), 并比较\(mac' \stackrel{?}{=} mac\), 如果相等则表示消息\(M\)是完整的。

对称密码

对称密码（Symmetric Encryption）是一种加密技术，使用相同的密钥对数据进行加密和解密，是最早的加密技术之一。对称加密的特点是加密和解密使用相同的密钥，速度快，适合大规模数据加密。

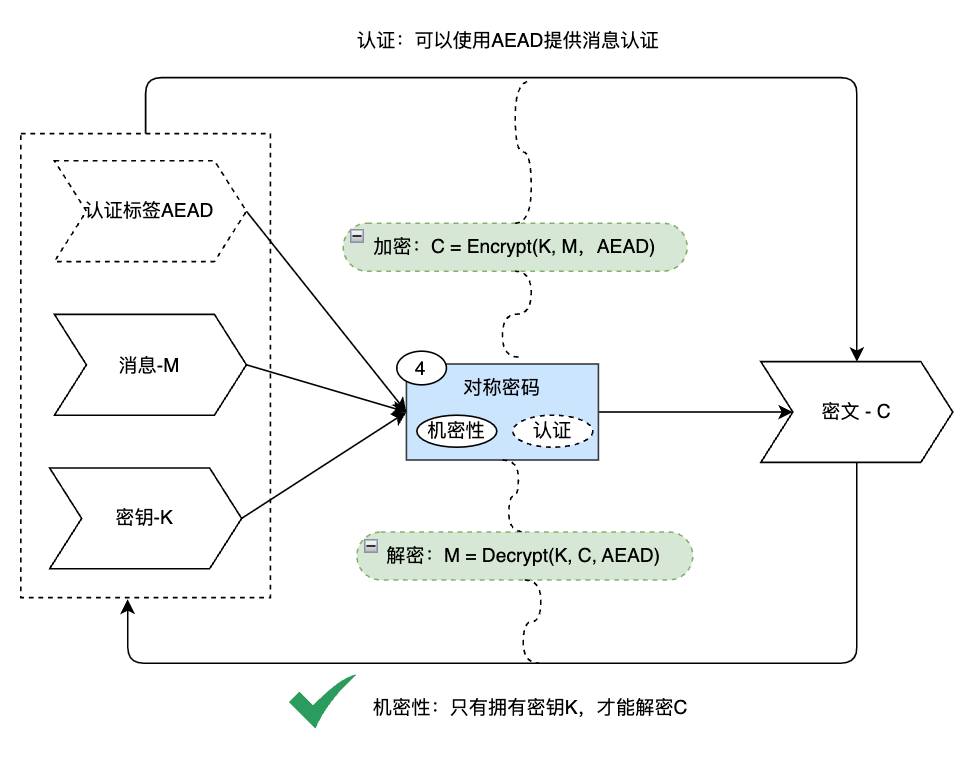
image

对称加密的特点是：

  • 对称加密使用相同的密钥对数据进行加密和解密，发送者和接收者需要共享密钥。
  • 对称加密速度快，适合大规模数据加密。
  • 常见的对称加密算法有DES、3DES、AES、RC4、IDEA、国密SM4等
  • 对称加密常用于数据加密、数据保护、数据传输等场景。

对称加密一般分为两大类：分组密码和流密码。分组密码是将明文分成固定长度的数据块，每个数据块使用相同的密钥进行加密，常见的分组密码有DES、IDEA、AES、SM4等。流密码是将明文和密钥进行按位异或运算，逐位加密，常见的流密码有RC4等。

特性 分组密码 流密码
加密方式 将明文分成固定长度的块进行加密 逐位对明文进行加密
密钥长度 密钥长度与明文长度一致，较短 密钥序列长度与明文长度一致，较长
应用场景 适用于需要高安全性的场景，如数据存储和网络通信 适用于需要高速加密和解密的场景，如无线通信和VPN
效率 可以并行对多个分组进行加密和解密，效率较高 逐位进行加密和解密，处理长明文时效率较低
安全性 提供较高的安全性，但密钥管理困难 安全性较高，但存在潜在的安全隐患，如重合攻击

分组密码有多种加密模式，对比如下：

分组加密模式 优点 缺点 备注
ECB
电子密码本模式		 简单、快速、支持并行计算 重复明文反映在密文中
不抵御重放攻击		 不应使用
CBC
密文分组链接		 不反映明文重复
支持解密并行计算		 解密时错误传播
加密不支持并行计算		 不推荐
CFB
密文反馈		 无需填充
支持解密并行计算		 加密不支持并行计算
错误传播		 不推荐
OFB
输出反馈		 无需填充
预先加密解密		 不支持并行计算
主动攻击可反转比特		 不推荐
CTR
计数器		 无需填充
预先加密解密
支持并行计算		 主动攻击可反转比特 推荐
GCM (Galois/Counter模式) 无需填充
结合计数器模式和AEAD认证机制，提供加密和数据完整性验证; </br> 高效且安全，适合需要认证的场景。		 实现相对复杂。 推荐

在实际应用中，分组加密模式CBC和CTR使用较为广泛，但目前来说GCM在整体表现上更加优异，如果不存在兼容问题，推荐使用GCM分组加密模式。

对称加密构造：

  • 加密

\[C = Encrypt(K, M, AEAD) \]

  • 解密

\[M = Decrypt(K, C, AEAD) \]

其中：\(K\)为密钥，\(M\)为明文，\(C\)为密文，\(Encrypt\)为加密算法，\(Decrypt\)为解密算法，\(AEAD\)为用于认证的额外数据。

对称加密使用流程：

  • 共享密钥\(K\)：首先发送者和接受者要共享密钥\(K\)，可以通过密钥协商协议生成、也可以由一方生成并安全传输给另一方。
  • 发送者使用密钥\(K\)对明文\(M\)进行加密，生成密文\(C\)，并将\(C\)发送给接受者。如果要对数据进行认证，还需要提供额外的认证数据\(AEAD\)。
  • 接受者使用密钥\(K\)对密文\(C\)进行解密，还原明文\(M\)，并验证认证数据\(AEAD\)，确保数据的完整性和真实性。

非对称密码

非对称密码: 非对称密码（Asymmetric Encryption）是一种加密技术，使用一对密钥（公钥和私钥）对数据进行加密和解密，是现代密码学的重要组成部分。非对称加密的特点是加密和解密使用不同的密钥，安全性高，适合密钥分发和数字签名。

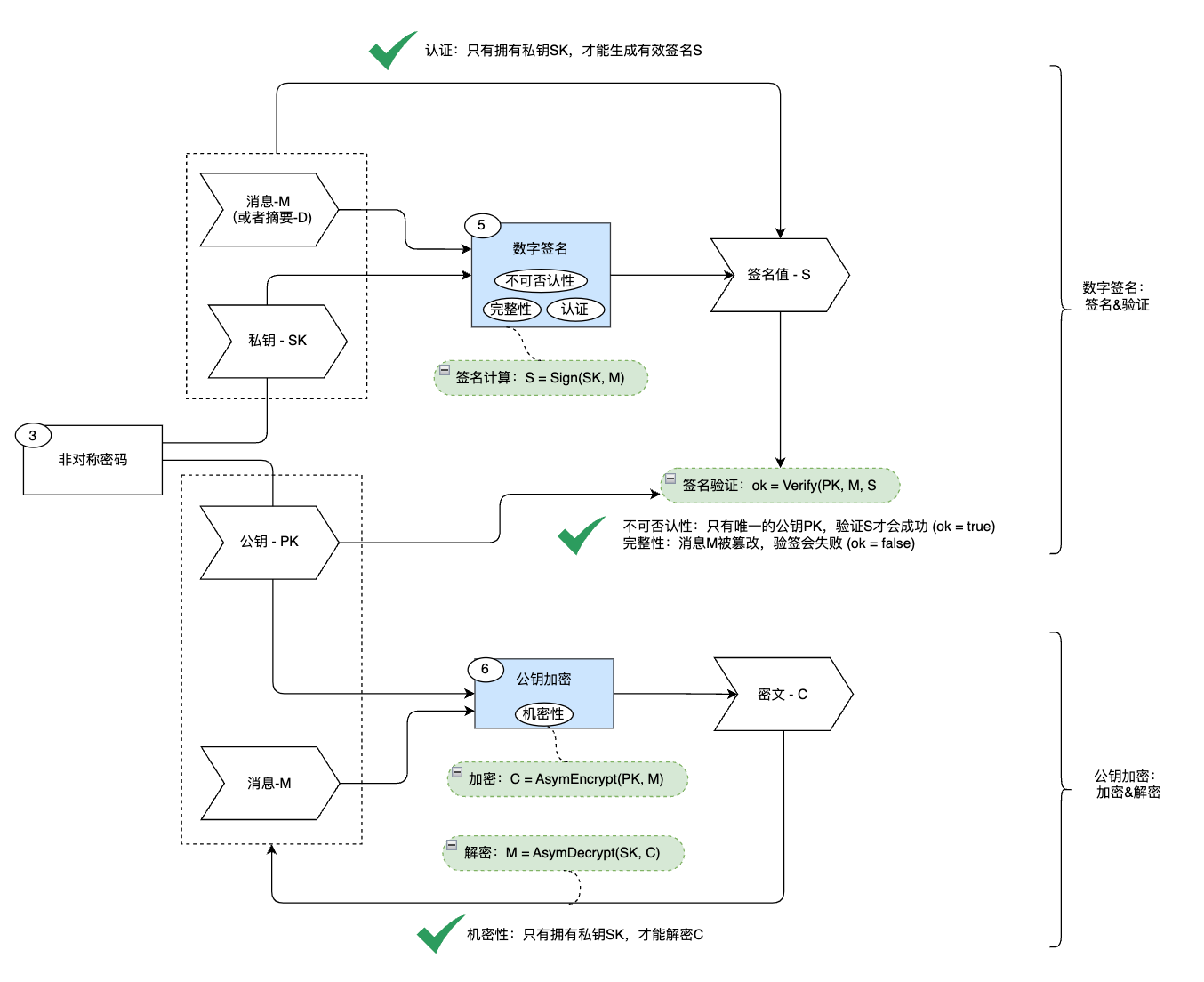
image

非对称密码的特点是：

  • 非对称加密（公钥加密）使用一对密钥（公钥和私钥）对数据进行加密和解密，发送者和接收者分别持有公钥和私钥，公钥用于加密，私钥用于解密。
  • 数字签名使用一对密钥（公钥和私钥）对数据进行签名和验证，发送者和接受者分别持有私钥和公钥，私钥用于签名，公钥用于验证。
  • 公钥加密速度慢，不适合大规模数据加密，多用于数字信封、密钥协商。
  • 常见的公钥加密算法有RSA、ElGamal、ECC等
  • 常见的数字签名算法有RSA、Elgamal、ECDSA、DSA、Schnorr等
  • 非对称密码常用于密钥协商、数据传输、身份鉴别等

公钥加密构造：

  • 加密：

\[C = AsymEncrypt(PK, M) \]

  • 解密：

\[M = AsymDecrypt(SK, C) \]

其中：\(PK\)为公钥，\(SK\)为私钥，\(M\)为明文，\(C\)为密文，\(AsymEncrypt\)为加密算法，\(AsymDecrypt\)为解密算法。

公钥加密使用流程：

  • 密钥分发：接受者生成一对密钥（公钥和私钥），将公钥发送给发送者，私钥保密。
  • 加密：发送者使用接受者的公钥对明文\(M\)进行加密，生成密文\(C\)，并将\(C\)发送给接受者。
  • 解密：接受者使用自己的私钥对密文\(C\)进行解密，还原明文\(M\)。

数字签名构造：

  • 签名：

\[S = Sign(SK, M) \]

  • 验证：

\[ok = Verify(PK, M, S) \]

其中：\(PK\)为公钥，\(SK\)为私钥，\(M\)为消息，\(S\)为签名，\(Sign\)为签名算法，\(Verify\)为验证算法。

数字签名使用流程：

  • 密钥分发：发送者生成一对密钥（公钥和私钥），将公钥发送给接受者，私钥保密。
  • 签名：发送者使用自己的私钥对消息\(M\)进行签名，生成签名\(S\)，并将\((M, S)\)发送给接受者。
  • 验证：接受者使用发送者的公钥对消息\(M\)和签名\(S\)进行验证，验证通过则表示消息是真实的。

数字证书

数字证书（Digital Certificate）是一种用于证明公钥拥有者身份的数字文件，通常由第三方机构（CA）颁发，用于保护公钥的安全性和真实性。数字证书包含公钥、证书持有者信息、证书颁发机构信息、证书有效期等信息。

数字证书一般采用X.509标准格式, 以下是一个数字证书示例：

➜ cat tmp.crt
-----BEGIN CERTIFICATE-----
MIIDCzCCArGgAwIBAgIDCzvxMAoGCCqBHM9VAYN1MIGKMQswCQYDVQQGEwJDTjEQ
MA4GA1UECBMHQmVpamluZzEQMA4GA1UEBxMHQmVpamluZzEfMB0GA1UEChMWd3gt
b3JnMS5jaGFpbm1ha2VyLm9yZzESMBAGA1UECxMJcm9vdC1jZXJ0MSIwIAYDVQQD
ExljYS53eC1vcmcxLmNoYWlubWFrZXIub3JnMB4XDTIxMDcwODAyMTk0M1oXDTI2
MDcwNzAyMTk0M1owgZAxCzAJBgNVBAYTAkNOMRAwDgYDVQQIEwdCZWlqaW5nMRAw
DgYDVQQHEwdCZWlqaW5nMR8wHQYDVQQKExZ3eC1vcmcxLmNoYWlubWFrZXIub3Jn
MQ8wDQYDVQQLEwZjb21tb24xKzApBgNVBAMTImNvbW1vbjEudGxzLnd4LW9yZzEu
Y2hhaW5tYWtlci5vcmcwWTATBgcqhkjOPQIBBggqgRzPVQGCLQNCAASVkTdOzqcQ
gcUapVaZLdY0voaLwJLC4VsW8TLUSlf2fB2Svv1ziLIu0820B0Hy2srmbGsv4p8z
YzzUJieqVkmfo4H9MIH6MA4GA1UdDwEB/wQEAwIBpjAPBgNVHSUECDAGBgRVHSUA
MCkGA1UdDgQiBCC0EHcZQ5jKeAZup7zn93OK3hzDrfzo5cAjP8coQ6dvijArBgNV
HSMEJDAigCD1tn8t4FRAXu6Gcn9qDx6BkI1n5Ngyrz4FD6i7jL5tTjBOBgNVHREE
RzBFgg5jaGFpbm1ha2VyLm9yZ4IJbG9jYWxob3N0giJjb21tb24xLnRscy53eC1v
cmcxLmNoYWlubWFrZXIub3JnhwR/AAABMC8GC4EnWI9kCx6PZAsEBCAwYjA3YzU4
Mjc1ZGE0YWY0YjQ1M2U0Mjg5OTA1N2I5ZTAKBggqgRzPVQGDdQNIADBFAiB7+V4u
TvnhR+oM05uZ45MaswjiKXPQvuzoMwDh14i63gIhAJxQnggig2UXg9Pz9ptU+k40
R36JDCfTS4w308er0ylX
-----END CERTIFICATE-----

➜  openssl x509 -in tmp.crt -noout -text
Certificate:
    Data:
        Version: 3 (0x2) # 证书版本
        Serial Number: 736241 (0xb3bf1) # 证书序列号
        Signature Algorithm: SM2-with-SM3 # 签名算法
        Issuer: C=CN, ST=Beijing, L=Beijing, O=org1, OU=root-cert, CN=ca..org # 颁发者
        Validity
            Not Before: Jul  8 02:19:43 2021 GMT # 有效期开始时间
            Not After : Jul  7 02:19:43 2026 GMT # 有效期结束时间
        Subject: C=CN, ST=Beijing, L=Beijing, O=org1, OU=common, CN=common1.org # 主体
        Subject Public Key Info: # 公钥信息
            Public Key Algorithm: id-ecPublicKey
                Public-Key: (256 bit)
                pub:
                    04:95:91:37:4e:ce:a7:10:81:c5:1a:a5:56:99:2d:
                    d6:34:be:86:8b:c0:92:c2:e1:5b:16:f1:32:d4:4a:
                    57:f6:7c:1d:92:be:fd:73:88:b2:2e:d3:cd:b4:07:
                    41:f2:da:ca:e6:6c:6b:2f:e2:9f:33:63:3c:d4:26:
                    27:aa:56:49:9f
                ASN1 OID: SM2 # 公钥算法
        X509v3 extensions: # 证书扩展信息
            X509v3 Key Usage: critical # 密钥用途
                Digital Signature, Key Encipherment, Certificate Sign, CRL Sign
            X509v3 Extended Key Usage: # 扩展密钥用途
                Any Extended Key Usage
            X509v3 Subject Key Identifier: # 主体密钥标识符
                B4:10:77:19:43:98:CA:78:06:6E:A7:BC:E7:F7:73:8A:DE:1C:C3:AD:FC:E8:E5:C0:23:3F:C7:28:43:A7:6F:8A
            X509v3 Authority Key Identifier: # 颁发者密钥标识符
                F5:B6:7F:2D:E0:54:40:5E:EE:86:72:7F:6A:0F:1E:81:90:8D:67:E4:D8:32:AF:3E:05:0F:A8:BB:8C:BE:6D:4E
            X509v3 Subject Alternative Name: # 主体备用名称
                DNS:chainmaker.org, DNS:localhost, DNS:common1.org, IP Address:127.0.0.1
            2.87.88.2020.11.30.2020.11.4:
                0b07c58275da4af4b453e42899057b9e
    Signature Algorithm: SM2-with-SM3 # 签名算法
    Signature Value: # 签名值，用于验证证书的真实性
        30:45:02:20:7b:f9:5e:2e:4e:f9:e1:47:ea:0c:d3:9b:99:e3:
        93:1a:b3:08:e2:29:73:d0:be:ec:e8:33:00:e1:d7:88:ba:de:
        02:21:00:9c:50:9e:08:22:83:65:17:83:d3:f3:f6:9b:54:fa

从上面我们可以看到数字证书包含了以下关键信息：

  • 证书版本、序列号、签名算法、颁发者、有效期、主题、公钥信息等。
  • 证书扩展信息，如密钥用途、扩展密钥用途、主题密钥标识符、颁发者密钥标识符、主题备用名称等。
  • 证书签名算法和签名值，用于验证证书的真实性。

数字证书的颁发

数字证书的颁发一般由证书颁发机构（Certificate Authority, CA）负责，CA是一种可信的第三方机构，负责验证证书持有者的身份，签发数字证书，并提供证书撤销服务。数字证书的申请、颁发、撤销等我们称之为PKI体系（Public Key Infrastructure）。

PKI体系如下：

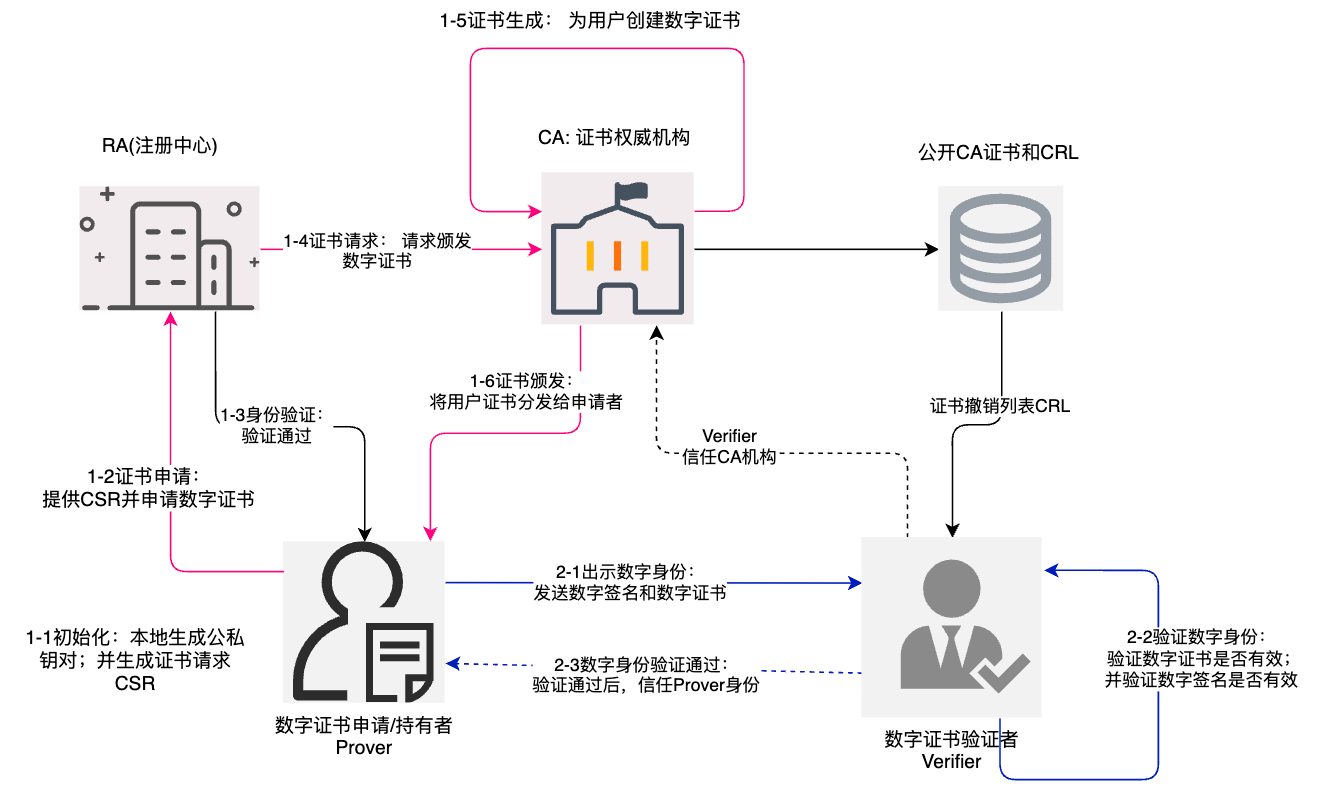
image

主要流程介绍：

  • 1-1初始化：证书申请者本地生成一对密钥（公钥和私钥），并生成证书请求（CSR），包含公钥、证书持有者信息等。
  • 1-2证书申请：证书申请者将证书请求（CSR）发送给RA，申请数字证书。
  • 1-3验证身份：RA对证书申请者的身份进行验证，包括个人身份、组织身份、域名身份等。
  • 1-4签发证书：RA将验证通过的证书请求发送给CA。
  • 1-5证书签发：CA对证书请求进行签名，生成数字证书。
  • 1-6证书颁发：CA将数字证书发送给证书申请者。
  • 2-1出示数字身份：证书持有者在通信时，使用私钥签名消息，并出示数字证书。
  • 2-2验证数字身份：通信对方(验证者)使用CA根证书验证数字证书的真实性，然后获取数字证书中的公钥并验证签名。
  • 2-3数字身份验证通过：数字证书&数字签名验证通过表明证书持有者的身份是真实的，验证者可以信任对方。

需要注意的是，在实际的PKI体系建设中：

  1. RA和CA大多数情况下是同一个机构，RA负责验证证书申请者的身份，CA负责签发数字证书。
  2. CA可以是根CA、中间CA，根CA负责签发中间CA的证书，中间CA负责签发终端用户的证书。所以数字证书的信任链是根CA->中间CA->终端用户多级结构。
  3. 证书撤销：数字证书的有效期有限，如果证书持有者的私钥泄露或者证书信息发生变更，需要撤销数字证书。CA会维护一个证书撤销列表（CRL），用于记录已经撤销的证书。在验证者验证数字证书时，会检查CRL列表，确保数字证书没有被撤销。
  4. 数字证书申请者可以选择自己生成密钥对，也可以选择CA生成密钥对，然后由CA在颁发证书时一同发送给申请者。

数字信封

数字信封（Digital Envelope）是一种用于保护数据机密性的加密技术，通常使用对称加密和非对称加密相结合的方式，实现数据的加密和解密。数字信封的基本思想是使用对称加密算法对数据进行加密，然后使用非对称加密算法对对称加密密钥进行加密，最后将加密后的数据和加密后的密钥一起发送给接收者。

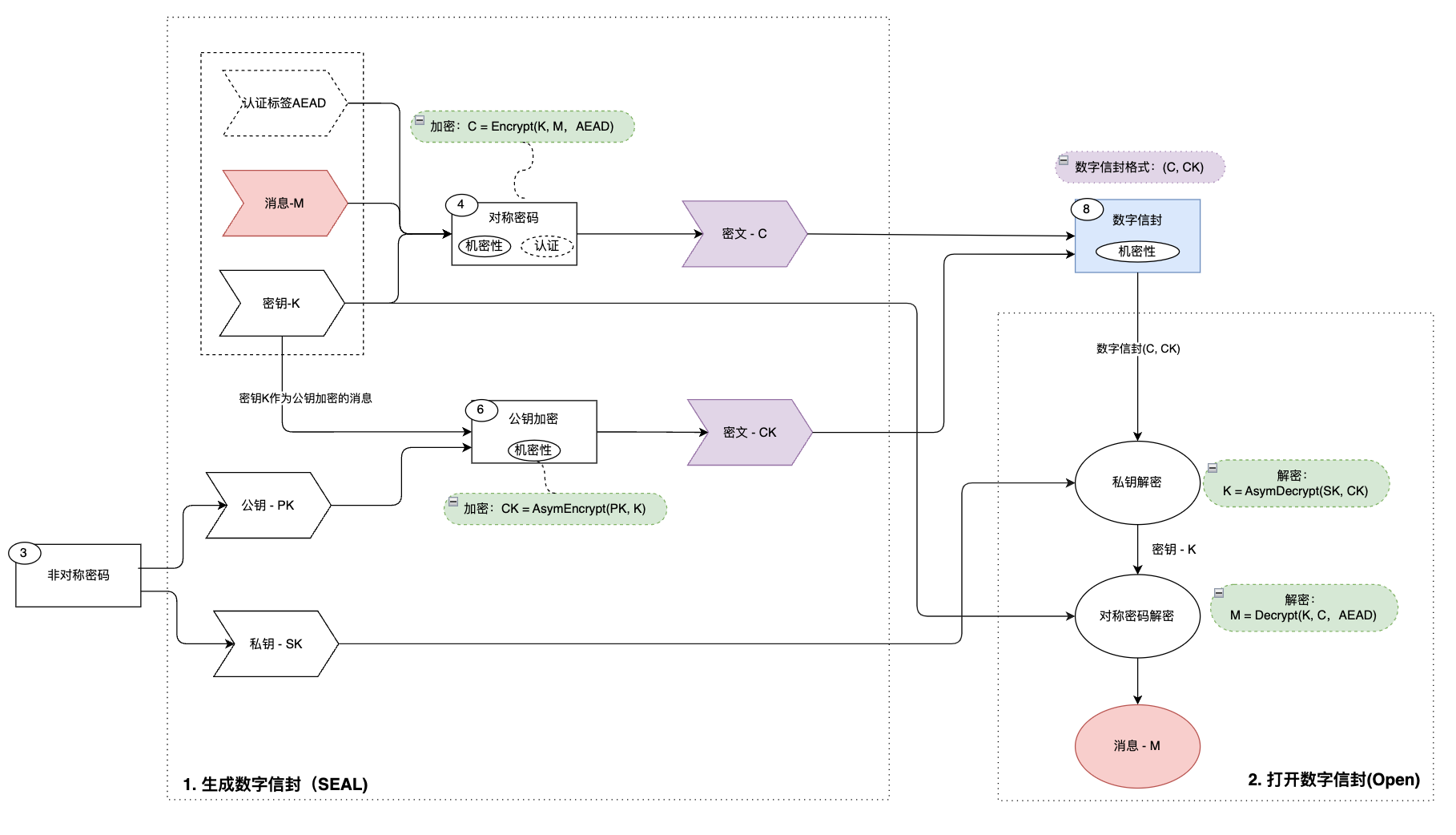
image

数字信封的特点是：

  • 数字信封使用对称加密算法对数据进行加密，速度快，适合大规模数据加密。
  • 数字信封使用非对称加密算法对对称加密密钥进行加密，解决了密钥分发的问题。
  • 数字信封常用于大数据共享、数据传输、数据存储等场景。

数字信封的构造：

  • 生成数字信封(SEAL)

\[C = Encrypt(K, M, AEAD) \quad \quad CK = AsymEncrypt(PK, K) \]

  • 打开数字信封(OPEN)

\[K = AsymDecrypt(SK, CK) \quad \quad M = Decrypt(K, C, AEAD) \]

其中：\(K\)为对称加密密钥，\(PK\)为公钥，\(SK\)为私钥，\(M\)为明文，\(C\)为密文，\(CK\)为加密后的对称加密密钥，\(Encrypt\)为对称加密算法，\(Decrypt\)为对称解密算法，\(AsymEncrypt\)为非对称加密算法，\(AsymDecrypt\)为非对称解密算法。\(AEAD\)为可选参数，用于认证的额外数据。

数字信封使用流程：

  • 公钥分发：数据接受者拥有一对密钥（公钥和私钥），将公钥发送给数据发送者。
  • 生成数字信封：数据发送者生成对称加密密钥\(K\)，使用\(K\)对明文\(M\)进行加密，生成密文\(C\)，然后使用接受者的公钥\(PK\)对\(K\)进行加密，生成加密后的密钥\(CK\)。并将\((C, CK)\)发送给接受者。
  • 打开数字信封：数据接受者使用自己的私钥\(SK\)对\(CK\)进行解密，获取对称加密密钥\(K\)，然后使用\(K\)对密文\(C\)进行解密，还原明文\(M\)。

密钥协商

密钥协商：密钥协商（Key Agreement）是一种用于双方协商共享密钥的技术，通常使用非对称加密算法实现，用于解决密钥分发的问题。密钥协商有多种算法，如DH算法、ECDH算法、ECDHE算法、RSA算法等，其中DH算法和ECDH算法是最常用的密钥协商算法、ECDHE算法是最安全密钥协商算法，它们都基于Diffie-Hellman协议,如下：

Diffie-Hellman协议：

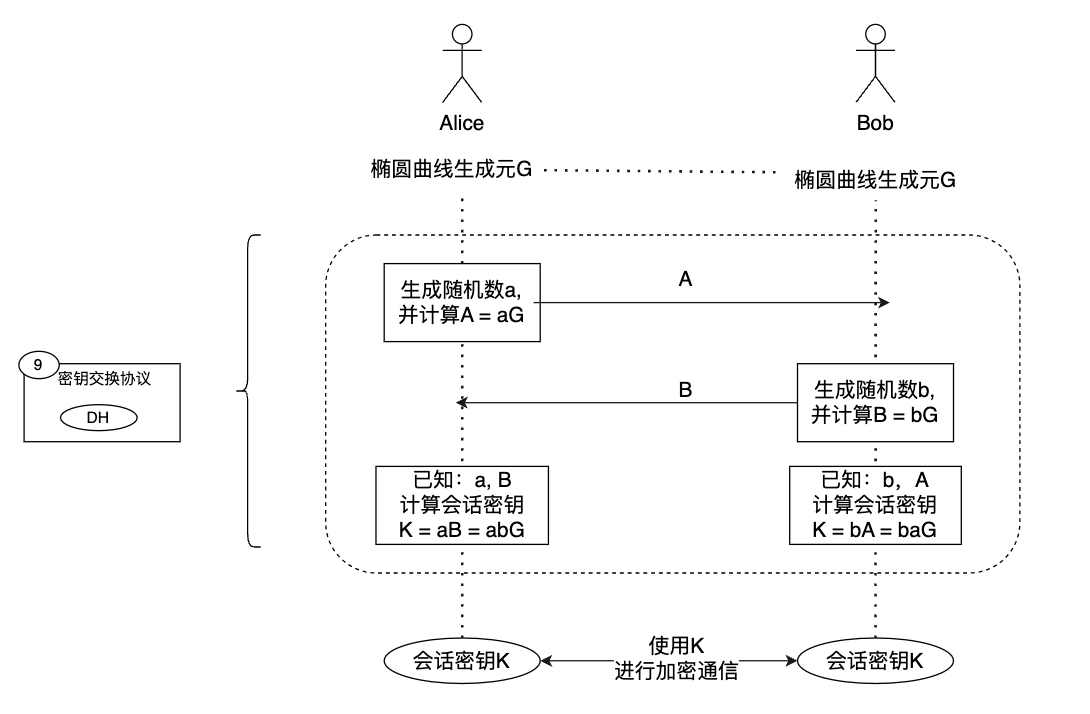
image

密钥协商的特点是：

  • 密钥协商使用非对称加密算法协商共享密钥，解决了密钥分发的问题。
  • Diffie-Hellman密钥交换算法大多基于离散对数问题，安全性高。
  • Diffie-Hellman密钥交换算法有很多变体，可以实现前向保密，如ECDHE具有前向保密性。
  • 密钥协商常用于TLS/SSL协议、IPSec协议、SSH协议等。
  • 存在中间人攻击问题

中间人攻击问题：

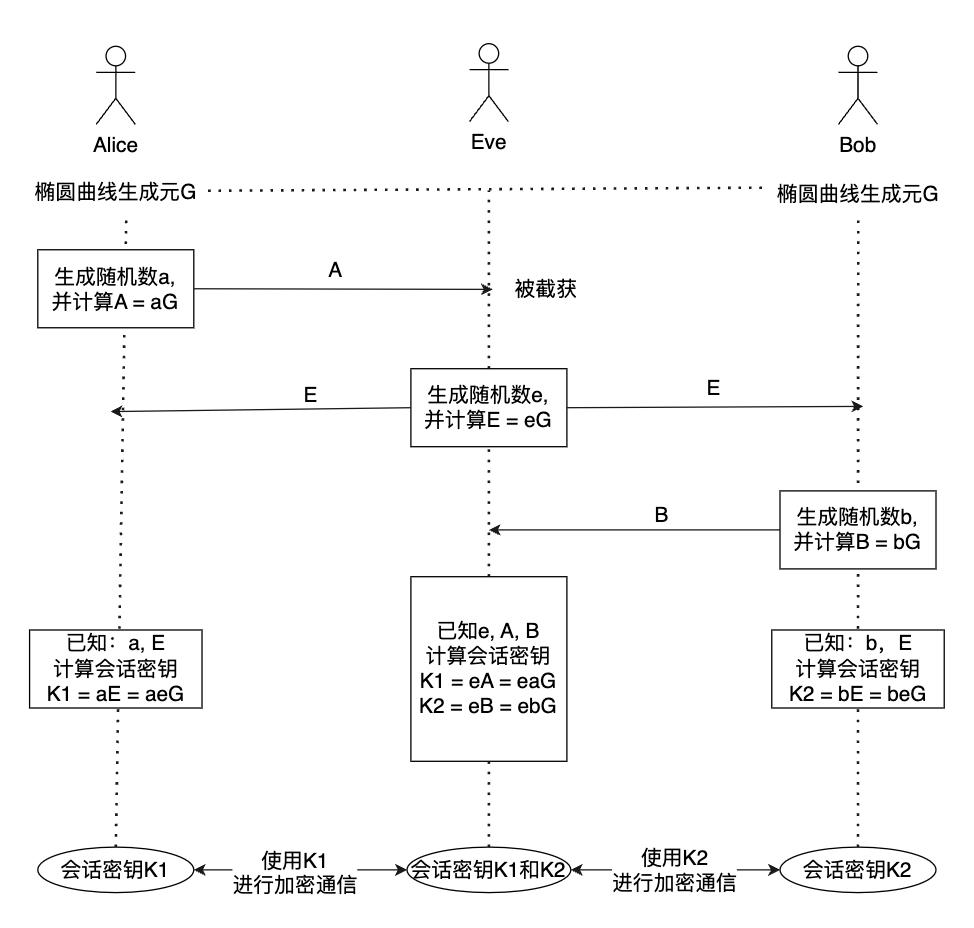
image

说明：

  • Eve攻击者可以截获并中断Alice和Bob的直接通信，充当中间人
  • Eve攻击者可以伪装成Bob，向Alice发送自己的公钥，同时伪装成Alice，向Bob发送自己的公钥
  • Alice和Bob分别使用Eve的公钥生成共享密钥，Eve可以解密和篡改Alice和Bob之间的通信

中间人攻击的解决方案：

  • 数字证书：Alice和Bob使用CA颁发的数字证书验证对方的身份，防止中间人攻击
  • 数字签名：Alice和Bob使用私钥对消息进行签名，接收方使用公钥验证签名（该公钥来自对方的数字证书），确保消息的真实性
  • 密钥协商：Alice和Bob使用密钥协商算法协商共享密钥，确保通信的安全性

SSL/TLS

SSL/TLS（Secure Sockets Layer/Transport Layer Security）是一种用于保护网络通信安全的加密协议，通常用于Web浏览器和Web服务器之间的安全通信。SSL/TLS协议使用对称加密、非对称加密、数字证书、数字信封以及密钥协商等技术，实现数据的加密、身份验证、数据完整性验证等功能。

SSL/TLS相关介绍可以参考之前的文章：

常见密码技术和推荐

密码技术 国际算法/协议 国产算法/协议 推荐 备注
哈希函数 MD5、SHA1、SHA2系列、SHA3系列 SM3 SHA2、SHA3、SM3 区块链主要使用SHA3系列的Keccak-256，主流的互联网系统使用SHA2-256
消息认证码 HMAC-MD5、HMAC-SHA1、HMAC-SHA256、HMAC-SHA3 HMAC-SM3 HMAC-SHA256、HMAC-SM3 无
对称密码 DES、3DES、AES、IDEA SM4 AES、SM4 AES为美国国家密码标准，当前使用最广泛的对称密码算法
非对称密码 RSA、ElGamal、ECC系列 SM2 ECC系列、SM2 SM2也是一种基于ECC的密码算法，此类算法密钥短、效率高，是目前主流的非对称密码算法；
此外RSA在金融系统以及较早建立的IT系统中也较为常见
数字证书 X.509标准 X.509标准 X.509标准 数字证书仅为一种数据格式规范，不单独涉及密码算法
数字信封 对称密码和非对称密码算法的组合算法 SM4和SM2的组合算法 AES-ECC组合，SM4-SM2组合 无
SSL/TLS TLS1.1、TLS1.2、TLS1.3 GMTLS1.1 TLS1.2、TLS1.3、GMTLS1.1 TLS1.2是当前最常见的TLS协议；
TLS1.3具有更高的安全性和握手效率,并且支持扩展国密算法；
GMTLS1.1是国产唯一的TLS协议,但国内还未普及；

结语

本文主要介绍了密码技术的应用背景和发展历程，并针对现代密码学中最常用的基础密码技术和应用进行了详细介绍，包括哈希函数、消息认证码、对称加密、非对称加密、数字证书、数字信封、密钥协商、SSL/TLS等，希望对大家有所帮助。

密码技术具有很深的理论基础，本文的内容主要针对入门级别，更深入的内容需要大家进一步学习和探索。密码学是信息安全的基础，掌握密码学的基础知识对于理解信息安全技术和应用非常重要。

参考文献

posted @ 2024-11-20 18:53  warm3snow  阅读(54)  评论(0)  编辑  收藏  举报