主页
微信公众号:密码应用技术实战
博客园首页:https://www.cnblogs.com/informatics/
GIT地址:https://github.com/warm3snow
简介
Bulletproof将范围证明转换为二次多项式表达\(t(X) = t_0 + t_1 \cdot X + t_2 \cdot X^2\),并通过多项式承诺和内积承诺的验证,完成了范围证明。回顾《Bulletproof范围证明之原理》,我们详细介绍了Bulletproof范围证明的构造和验证流程。本文将进一步介绍Bulletproof范围证明的优化技术 - 折半算法
本文组织如下:
- 术语定义
- Bulletproof复杂度分析
- Bulletproof折半算法
- 总结
- 参考文献
术语定义
- \(p\)和\(q\):分别表示两个大素数
- \(Z_p\):表示模\(p\)的整数环
- \(Z_p^*\):表示模\(p\)的整数环中的所有与\(p\)互素的元素, 即非零元素
- \(G\):阶为\(p\)的循环群, 如果:\(g \in G, G = \{1, g, g^2, ..., g^{p-1}\} \equiv Z_p\), 则\(g\)是\(G\)的生成元
- \(G^n\)和\(Z_p^n\):分别表示群\(G\)上的n维向量空间和\(Z_p\)上的n维向量空间
- \(h^r \mathbf{g}^{\mathbf{x}}\) = \(h^r \cdot \prod_{i=1}^{n} g_i^{x_i} = h^r \cdot g_1^{x_1} \cdot g_2^{x_2} \cdot ... \cdot g_n^{x_n}\): 表示向量\(\mathbf{x}\)的Pedersen承诺值
- \(\mathbf{g}^{\mathbf{a}}{\mathbf{h}}^{\mathbf{b}} = \prod_{i=1}^{n} g_i^{a_i} \cdot h_i^{b_i}\): 表示向量\(\mathbf{a}\)和\(\mathbf{b}\)的Pedersen承诺值
- \(\langle \mathbf{a}, \mathbf{b} \rangle = \mathbf{a} \cdot \mathbf{b} = \sum_{i=1}^{n} a_i \cdot b_i\): 表示向量\(\mathbf{a}\)和\(\mathbf{b}\)的内积。
- \(\mathbf{a} \circ \mathbf{b} = (a_1 \cdot b_1, a_2 \cdot b_2, ..., a_n \cdot b_n)\): 表示向量\(\mathbf{a}\)和\(\mathbf{b}\)的哈达玛积。
- \(\mathbf{a_{[:n']}} = (a_1, a_2, ..., a_{n'}) \in F^{n'}\) 和 \(\mathbf{a_{[n':]}} = (a_{n'+1}, a_{n'+2}, ..., a_n) \in F^{n-n'}\): 表示向量\(\mathbf{a}\)的前\(n'\)个元素和后\(n-n'\)个元素。
- \(P\)和\(V\): 分别表示证明生成者Prover和证明验证者Verifier
Bulletproof复杂度分析
在上一篇文章《Bulletproof范围证明之原理》中,我们介绍了Bulletproof向量内积证明,Bulletproof使用向量内积证明来进行范围证明,流程如下:
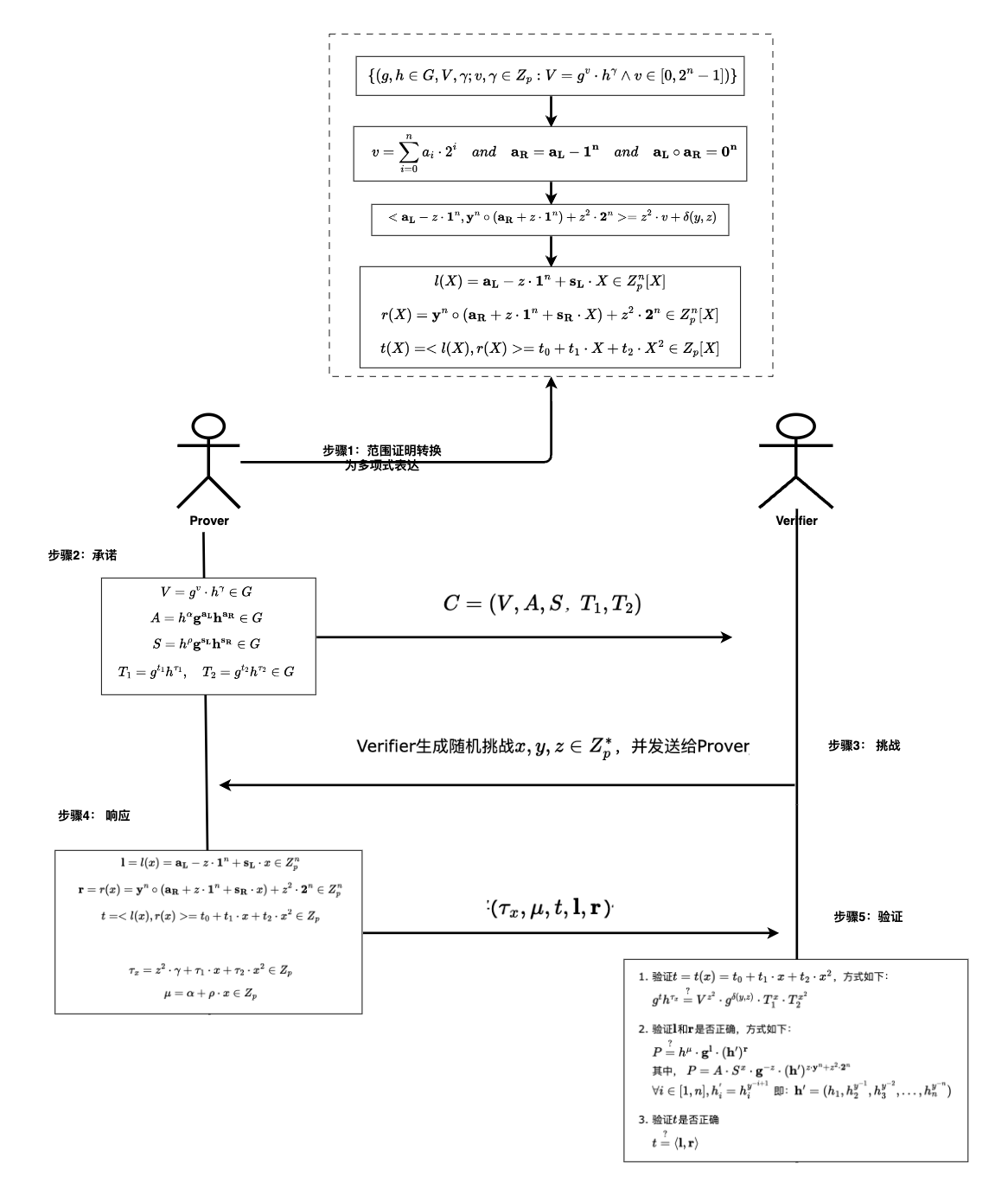
分析上图中的通信数据包可以发现,交互式Bulletproof向量内积证明过程中,Prover和Verifier需要发送的数据包包括:
- 承诺\(C = (V, A, S, T_1, T_2)\), 其中\(V, A, S, T_1, T_2 \in G\), 复杂度为\(O(1)\)
- Verifier需要发送的数据包括:挑战\((x, y, z)\), 其中\(x, y, z \in Z_p^*\), 复杂度为\(O(1)\)
- 响应\((\tau_x, \mu, t, \mathbf{l}, \mathbf{r})\), 其中\(\tau_x, \mu, t \in Z_p\), \(\mathbf{l}, \mathbf{r} \in Z_p^n\), 复杂度为\(O(2n)\)
综上,未优化版本的Bulletproof向量内积证明通信复杂度为\(O(2n)\)。复杂度主要来自于Prover发送的响应\((\mathbf{l}, \mathbf{r})\),其中\(\mathbf{l}\)和\(\mathbf{r}\)是长度为\(n\)的向量。
Bulletproof折半算法
Bulletproof折半算法是Bulletproof的一种优化技木,主要用于减少Bulletproof范围证明的通信复杂度,并实现了\(O(2\log_2{n})\)的通信复杂度。Bulletproof折半算法的核心思想是通过递归的方式,不断将向量\(\mathbf{l}\)和\(\mathbf{r}\)折半,直到两个向量长度都为1,最终发送\(O(2\log_2{n})\)个长度为1的数据包,从而实现了数据的压缩。
折半算法
Bulletproof折半算法基于改进的向量内积证明,下面我们将详细介绍Bulletproof折半算法的优化原理。
改进的向量内积
假设\(\mathbf{g}\)和\(\mathbf{h}\)是两个独立的\(G\)生成元,标量\(c \in Z_p\),并有\(P \in G\),向量内积证明的目标是Prover向Verifier证明自己知道向量\(\mathbf{a}, \mathbf{b} \in Z_p^n\), 满足以下关系:
\[P = {\mathbf{g}}^{\mathbf{a}}{\mathbf{h}}^{\mathbf{b}} \quad and \quad c = \langle \mathbf{a}, \mathbf{b} \rangle
\]
其中:
- \(P\)是\(\mathbf{a}, \mathbf{b}\)的向量Pedersen承诺。
- \(c\)表示\(\mathbf{a}, \mathbf{b}\)的向量内积
以上的向量关系可以转换为下面的证明系统:
\[\{(\mathbf{g},\mathbf{h} \in G^n, P \in G, c \in Z_p; \mathbf{a}, \mathbf{b} \in Z_p^n): P = {\mathbf{g}}^{\mathbf{a}}{\mathbf{h}}^{\mathbf{b}} \land c = \langle \mathbf{a}, \mathbf{b} \rangle \}
\]
在上述证明系统中:
- Prover可以直接将\(\mathbf{a}, \mathbf{b} \in Z_p^n\)发送给Verifier, Verifier重新计算\(P\)并检查是否正确,这种承诺的明文打开和验证方式显然是可以的。
- Prover需要向Verifier发送\(2n\)个元素。
在Bulletproof中,将以上证明系统转换为以下等价的证明系统:
\[\{(\mathbf{g},\mathbf{h} \in G^n, u, P \in G, c \in Z_p; \mathbf{a}, \mathbf{b} \in Z_p^n): P = {\mathbf{g}}^{\mathbf{a}}{\mathbf{h}}^{\mathbf{b}} \cdot u^{\langle \mathbf{a}, \mathbf{b} \rangle} \}
\]
其中\(u\)是\(G\)的独立且公开的生成元。
折半算法
H函数
在Bulletproof折半算法中,引入了一个特殊的功能函数\(H: Z_p^{2n+1} \rightarrow G\)
\[H(\mathbf{w}, \mathbf{x}, \mathbf{y}, \mathbf{z}, c) = {\mathbf{g}}_{[:n']}^{\mathbf{w}} \cdot {\mathbf{g}}_{[n':]}^{\mathbf{x}} \cdot {\mathbf{h}}_{[:n']}^{\mathbf{y}} \cdot {\mathbf{h}}_{[n':]}^{\mathbf{z}} \cdot u^c \in G
\]
其中:
- \(n' = n/2\), 即\({\mathbf{g}}_{[:n']}\)表示向量\(\mathbf{g}\)的前\(n/2\)个元素,\({\mathbf{g}}_{[n':]}\)表示向量\(\mathbf{g}\)的后\(n/2\)个元素。\({\mathbf{h}}_{[:n']}, {\mathbf{h}}_{[n':]}\)同理
- 输入参数为五元组\(\{\mathbf{w}, \mathbf{x}, \mathbf{y}, \mathbf{z} \in Z_p^{n'}, c \in Z_p \}\)
- 输出为群\(G\)中的元素
上述\(H\)函数有一个重要性质: 加法同态。即:
\[H(\mathbf{w1}, \mathbf{x1}, \mathbf{y1}, \mathbf{z1}, c1) \cdot H(\mathbf{w2}, \mathbf{x2}, \mathbf{y2}, \mathbf{z2}, c2) = H(\mathbf{w1 + w2}, \mathbf{x1 + x2}, \mathbf{y1 + y2}, \mathbf{z1 + z2}, c1 + c2)
\]
同态性证明:
\[H(\mathbf{w1}, \mathbf{x1}, \mathbf{y1}, \mathbf{z1}, c1) \cdot H(\mathbf{w2}, \mathbf{x2}, \mathbf{y2}, \mathbf{z2}, c2)
\]
\[= {\mathbf{g}}_{[:n']}^{\mathbf{w1}} \cdot {\mathbf{g}}_{[n':]}^{\mathbf{x1}} \cdot {\mathbf{h}}_{[:n']}^{\mathbf{y1}} \cdot {\mathbf{h}}_{[n':]}^{\mathbf{z1}} \cdot u^{c1} \cdot {\mathbf{g}}_{[:n']}^{\mathbf{w2}} \cdot {\mathbf{g}}_{[n':]}^{\mathbf{x2}} \cdot {\mathbf{h}}_{[:n']}^{\mathbf{y2}} \cdot {\mathbf{h}}_{[n':]}^{\mathbf{z2}} \cdot u^{c2}
\]
\[= {\mathbf{g}}_{[:n']}^{\mathbf{w1} + \mathbf{w2}} \cdot {\mathbf{g}}_{[n':]}^{\mathbf{x1} + \mathbf{x2}} \cdot {\mathbf{h}}_{[:n']}^{\mathbf{y1} + \mathbf{y2}} \cdot {\mathbf{h}}_{[n':]}^{\mathbf{z1} + \mathbf{z2}} \cdot u^{c1 + c2}
\]
\[= H(\mathbf{w1 + w2}, \mathbf{x1 + x2}, \mathbf{y1 + y2}, \mathbf{z1 + z2}, c1 + c2)
\]
等价转换
按照\(H\)函数的定义,我们可以将证明系统中的\(P\)重写为:
\[P = {\mathbf{g}}^{\mathbf{a}}{\mathbf{h}}^{\mathbf{b}} \cdot u^{\langle \mathbf{a}, \mathbf{b} \rangle} = H(\mathbf{a_{[:n']}}, \mathbf{a_{[n':]}}, \mathbf{b_{[:n']}, \mathbf{b_{[n':]}, \langle \mathbf{a}, \mathbf{b} \rangle} }) \in G
\]
等式证明:
\[P = {\mathbf{g}}^{\mathbf{a}}{\mathbf{h}}^{\mathbf{b}} \cdot u^{\langle \mathbf{a}, \mathbf{b} \rangle} = \prod g_i^{a_i} \cdot \prod h_i^{b_i} \cdot u^{\langle \mathbf{a}, \mathbf{b} \rangle}
\]
\[= \prod_{i=1}^{n'} g_i^{a_i} \cdot \prod_{i=n'+1}^{n} g_i^{a_i} \cdot \prod_{i=1}^{n'} h_i^{b_i} \cdot \prod_{i=n'+1}^{n} h_i^{b_i} \cdot u^{\langle \mathbf{a}, \mathbf{b} \rangle}
\]
\[= {\mathbf{g}}_{[:n']}^{\mathbf{a_{[:n']}}} \cdot {\mathbf{g}}_{[n':]}^{\mathbf{a_{[n':]}}} \cdot {\mathbf{h}}_{[:n']}^{\mathbf{b_{[:n']}}} \cdot {\mathbf{h}}_{[n':]}^\mathbf{b_{[n':]}} \cdot u^{\langle \mathbf{a}, \mathbf{b} \rangle}
\]
\[= H(\mathbf{a_{[:n']}}, \mathbf{a_{[n':]}}, \mathbf{b_{[:n']}, \mathbf{b_{[n':]}, \langle \mathbf{a}, \mathbf{b} \rangle} }) \in G
\]
折半算法构造
Bulletproof折半算法的构造流程如下:
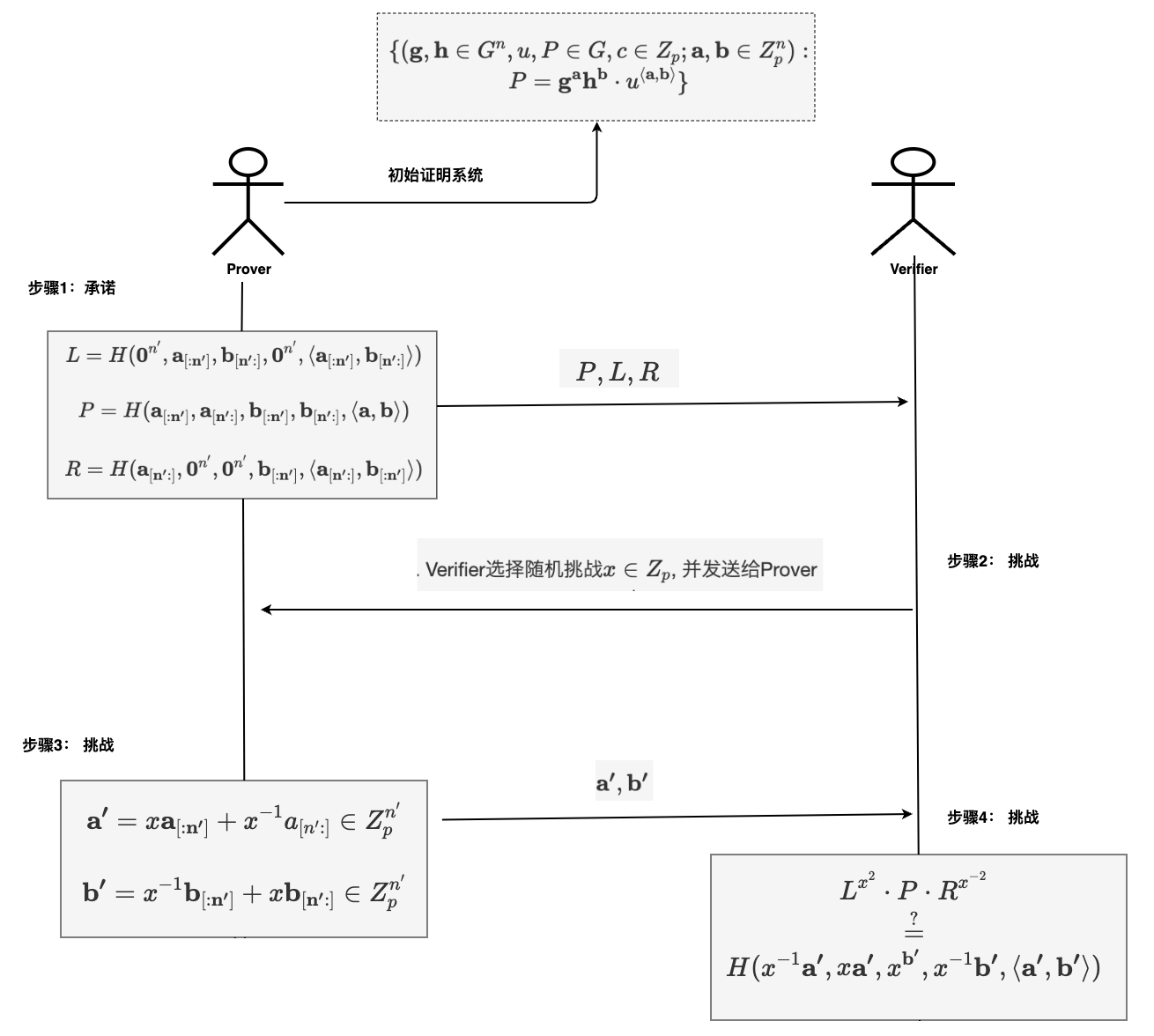
- Prover计算\(L, R \in G\), 并发送给Verifier
\[L = H(\mathbf{0}^{n'}, \mathbf{a_{[:n']}}, \mathbf{b_{[n':]}},\mathbf{0}^{n'}, \langle \mathbf{a_{[:n']}}, \mathbf{b_{[n':]}} \rangle)
\]
\[= {\mathbf{g}}_{[:n']}^{\mathbf{0}^{n'}} \cdot {\mathbf{g}}_{[n':]}^{\mathbf{a_{[:n']}}} \cdot {\mathbf{h}}_{[:n']}^{\mathbf{b_{[:n']}}} \cdot {\mathbf{h}}_{[n':]}^{\mathbf{0}^{n'}} \cdot u^{\langle \mathbf{a_{[:n']}}, \mathbf{b_{[n':]}} \rangle}
\]
\[R = H(\mathbf{a_{[n':]}}, \mathbf{0}^{n'}, \mathbf{0}^{n'}, \mathbf{b_{[:n']}}, \langle \mathbf{a_{[n':]}}, \mathbf{b_{[:n']}} \rangle)
\]
\[= {\mathbf{g}}_{[:n']}^{\mathbf{a_{[n']}}} \cdot {\mathbf{g}}_{[n':]}^{\mathbf{0}^{n'}} \cdot {\mathbf{h}}_{[:n']}^{\mathbf{0}^{n'}} \cdot {\mathbf{h}}_{[n':]}^{\mathbf{b_{[:n']}}}\cdot u^{\langle \mathbf{a_{[n':]}}, \mathbf{b_{[:n']}} \rangle}
\]
- Verifier选择随机挑战\(x \in Z_p\), 并发送给Prover
- Prover计算\(\mathbf{a'}, \mathbf{b'} \in Z_p^{n'}\), 并发送给Verifier
\[\mathbf{a'} = x\mathbf{a_{[:n']}} + x^{-1}\mathbb{a_{[n':]}} \in Z_p^{n'}
\]
\[\mathbf{b'} = x^{-1}\mathbf{b_{[:n']}} + x\mathbf{b_{[n':]}} \in Z_p^{n'}
\]
- 基于\(L, R, \mathbf{a'}, \mathbf{b'}\), Verifier验证以下等式是否成立:
\[L^{x^2} \cdot P \cdot R^{x^{-2}} \stackrel{?}{=} H(x^{-1}\mathbf{a'}, x\mathbf{a'}, x^\mathbf{b'}, x^{-1}\mathbf{b'}, \langle \mathbf{a'}, \mathbf{b'} \rangle)
\]
- 注:等式中的\(P\)是Prover发送的向量内积证明的承诺值
正确性验证
已知:
\[L = H(\mathbf{0}^{n'}, \mathbf{a_{[:n']}}, \mathbf{b_{[n':]}},\mathbf{0}^{n'}, \langle \mathbf{a_{[:n']}}, \mathbf{b_{[n':]}} \rangle)
\]
\[P = H(\mathbf{a_{[:n']}}, \mathbf{a_{[n':]}}, \mathbf{b_{[:n']}, \mathbf{b_{[n':]}, \langle \mathbf{a}, \mathbf{b} \rangle}})
\]
\[R = H(\mathbf{a_{[n':]}}, \mathbf{0}^{n'}, \mathbf{0}^{n'}, \mathbf{b_{[:n']}}, \langle \mathbf{a_{[n':]}}, \mathbf{b_{[:n']}} \rangle)
\]
根据\(H\)函数的同态性质,容易计算:
\[L^{x^2} \cdot P \cdot R^{x^{-2}}
\]
\[= H(x^2\mathbf{0}^{n'} + \mathbf{a_{[:n']}} + x^{-2}\mathbf{a_{[n':]}}, x^2\mathbf{a_{[:n']}} + \mathbf{a_{[n':]}} + x^{-2}\mathbf{0}^{n'}, x^2\mathbf{b_{[n']}} + \mathbf{b_{[:n']} + x^{-2}\mathbf{0}^{n'}}, x^2\mathbf{0}^{n'}+\mathbf{b_{[n':]}}+x^{-2}\mathbf{b_{[:n']}}, x^2 \langle \mathbf{a_{[:n']}}, \mathbf{b_{[n':]}} \rangle + \langle \mathbf{a}, \mathbf{b} \rangle + x^{-2}\langle \mathbf{a_{[n':]}}, \mathbf{b_{[:n']}} \rangle)
\]
\[= H(\mathbf{a_{[:n']}} + x^{-2}\mathbf{a_{[n':]}}, x^2\mathbf{a_{[:n']}} + \mathbf{a_{[n':]}}, x^2\mathbf{b_{[n']}} + \mathbf{b_{[:n']}}, \mathbf{b_{[n':]}}+x^{-2}\mathbf{b_{[:n']}}, x^2 \langle \mathbf{a_{[:n']}}, \mathbf{b_{[n':]}} \rangle + \langle \mathbf{a}, \mathbf{b} \rangle + x^{-2}\langle \mathbf{a_{[n':]}}, \mathbf{b_{[:n']}} \rangle)
\]
\[= H(x^{-1}\mathbf{a'}, x\mathbf{a'}, x^\mathbf{b'}, x^{-1}\mathbf{b'}, x^2 \langle \mathbf{a_{[:n']}}, \mathbf{b_{[n':]}} \rangle + \langle \mathbf{a}, \mathbf{b} \rangle + x^{-2}\langle \mathbf{a_{[n':]}}, \mathbf{b_{[:n']}} \rangle)
\]
由于:
\[\langle \mathbf{a'}, \mathbf{b'} \rangle = \langle x\mathbf{a_{[:n']}} + x^{-1}\mathbb{a_{[n':]}}, x^{-1}\mathbf{b_{[:n']}} + x\mathbf{b_{[n':]}} \rangle
\]
\[= (x\mathbf{a_{[:n']}} + x^{-1}\mathbb{a_{[n':]}}) \cdot (x^{-1}\mathbf{b_{[:n']}} + x\mathbf{b_{[n':]}})
\]
\[= x^2 \langle \mathbf{a_{[:n']}}, \mathbf{b_{[n':]}} \rangle + \mathbf{a_{[:n']}}\mathbf{b_{[:n']}} + \mathbf{a_{[n':]}}\mathbf{b_{[n':]}} + x^{-2}\langle \mathbf{a_{[n':]}}, \mathbf{b_{[:n']}}\rangle
\]
\[= x^2 \langle \mathbf{a_{[:n']}}, \mathbf{b_{[n':]}} \rangle + \langle \mathbf{a}, \mathbf{b} \rangle + x^{-2}\langle \mathbf{a_{[n':]}}, \mathbf{b_{[:n']}} \rangle
\]
因此,我们可以得出:
\[L^{x^2} \cdot P \cdot R^{x^{-2}} = H(x^{-1}\mathbf{a'}, x\mathbf{a'}, x^\mathbf{b'}, x^{-1}\mathbf{b'}, \langle \mathbf{a'}, \mathbf{b'} \rangle)
\]
综上,verifier可以成功验证步骤4中的等式,即折半算法的正确性。
复杂度分析
通过折半算法,在通信过程中,Prover只发送了\((P, L, R, \mathbf{a'}, \mathbf{b'}\)), 其中
- \((P, L, R) \in G\), 通信复杂度为\(O(1)\)
- \(\mathbf{a'}, \mathbf{b'} \in Z_p^{n'}\), 通信复杂度为\(O(n') = O(n/2)\)
因此通过一轮折半算法,可以将直接发送\(\mathbf{a}, \mathbf{b} \in Z_p^{n}\)的复杂度减半。
递归折半算法
通过递归折半的方式,我们可以进一步降低复杂度:
- Prover可以在\((\mathbf{a}', \mathbf{b}')\)基础上继续执行折半算法
- 通过\(\log_2n\)次折半(即:向量长度每次减半),可以将\(\mathbf{a}, \mathbf{b} \in Z_p^{n}\)折半为两个元素\(a, b\in Z_p\)
- 每次执行折半算法,Prover需要重新生成\(L,R\)
由于交互式证明可以通过Fiat-Shamir方法转换为非交互式证明,因此在整个递归折半算法中,Prover仅需要发送以下消息给Verifier:
\[(L_1, R_1), ..., (L_{\log_2n}, R_{\log_2n}), a, b
\]
- \((L_i, R_i), \forall i \in [1:\log_2n]\)表示第\(i\)次执行折半算法生成, 所有\((L, R)\)复杂度:\(2\log_2n\)
- \(a, b\)为两个元素,复杂度为\(O(1)\)
因此Bulletproof通过递归折半算法,成功将通信复杂度降低为\(2\log_2n\)。
结语
本文详细分析了Bulletproof范围证明的优化技术 - 折半算法。通过引入\(H\)函数和递归折半算法,Bulletproof成功将通信复杂度降低为\(O(2\log_2n)\)。折半算法的优化思想可以应用于其他范围证明系统,从而进一步提高范围证明的效率。除了以上优化技术外,Bulletproof的多个范围证明也可以通过批量验证等技术进一步提高效率。
本文未对Bulletproof递归折半算法构造进行详细证明,感兴趣的读者可以参考《Bulletproofs: Short Proofs for Confidential Transactions and More》进行深入学习。
参考文献





 浙公网安备 33010602011771号
浙公网安备 33010602011771号