Bulletproof范围证明之原理

主页

微信公众号：密码应用技术实战
博客园首页：https://www.cnblogs.com/informatics/
GIT地址：https://github.com/warm3snow

简介

在《门罗币隐私保护之机密交易》中，我们提到了Bulletproof范围证明技术，用于证明交易金额(Pedersen密文形式)在一个合理的范围内。Bulletproof范围证明是一种零知识范围证明技术。通常称为 Zero Knowledge Range Proof，简称 ZKRP。ZKRP与通用的零知识证明技术相比，具有如下特点：

高效性：ZKRP证明的大小和验证时间都比较小
通用性：ZKRP通用性较差，主要用于证明某个值在一个合理的范围内的场景，如：机密交易、身份验证、隐私投票、隐私竞拍等。

ZKRP实现方案很多，除了通用的ZKP技术外，还有Bulletproof、ZK Set Membership、Hash chains等技术。但由于Bulletproof范围证明具有效率高、透明设置、可聚合性，与Pedersen承诺的兼容性等特点，在实践中最受欢迎。Bulletproof范围证明及其优化涉及到多个技术细节，如：内积证明、折半算法、非交互式证明等。

本文将对Bulletproof范围证明技术中的内积证明进行详细介绍，包括基本构造、证明生成和验证流程等。

本文内容组织如下：

术语定义
范围证明形式化表示
向量内积表示
范围证明多项式表达
Bulletproof交互式范围证明
结语
参考文献

术语定义

$p$和$q$：分别表示两个大素数
$Z_p$：表示模$p$的整数环
$Z_p^*$：表示模$p$的整数环中的所有与$p$互素的元素, 即非零元素
$G$：阶为$p$的循环群, 如果：$g \in G, G = \{1, g, g^2, ..., g^{p-1}\} \equiv Z_p$, 则$g$是$G$的生成元
$G^n$和$Z_p^n$：分别表示群$G$上的n维向量空间和$Z_p$上的n维向量空间
$h^r \mathbf{g}^{\mathbf{x}}$ = $h^r \cdot \prod_{i=1}^{n} g_i^{x_i} = h^r \cdot g_1^{x_1} \cdot g_2^{x_2} \cdot ... \cdot g_n^{x_n}$: 表示向量$\mathbf{x}$的Pedersen承诺值
$\langle \mathbf{a}, \mathbf{b} \rangle = \mathbf{a} \cdot \mathbf{b} = \sum_{i=1}^{n} a_i \cdot b_i$: 表示向量$\mathbf{a}$和$\mathbf{b}$的内积。
$\mathbf{a} \circ \mathbf{b} = (a_1 \cdot b_1, a_2 \cdot b_2, ..., a_n \cdot b_n)$: 表示向量$\mathbf{a}$和$\mathbf{b}$的哈达玛积。
$p(X) = \sum_{i=0}^{d} \mathbf{p_i} \cdot X^i \in Z_p[X]$: 表示模$p$的向量多项式，其中$\mathbf{p_i} \in Z_p^n$。
$\langle l(X), r(X) \rangle = \sum_{i=0}^{d} \sum_{j=0}^{i} \langle l_i, r_j \rangle \cdot X^{i+j}$: 表示向量多项式$l(X)$和$r(X)$的内积。
$t(X) = \langle l(X), r(X) \rangle$: 令$t(X)$等于向量多项式$l(X)$和$r(X)$的内积，则$\forall x \in Z_p, t(x) = \langle l(x), r(x) \rangle$。
$\mathbf{a_{[:n']}} = (a_1, a_2, ..., a_{n'}) \in F^{n'}$ 和 $\mathbf{a_{[n':]}} = (a_{n'+1}, a_{n'+2}, ..., a_n) \in F^{n-n'}$: 表示向量$\mathbf{a}$的前$n'$个元素和后$n-n'$个元素。
$\mathbf{k^n} = (k^0, k^1, k^2, ..., k^{n-1})$: 表示长度为$n$的向量$\mathbf{k}$，其中$k^i \in Z_p*$。
$P$和$V$: 分别表示证明生成者Prover和证明验证者Verifier

Bulletproof范围证明

Bulletproof范围证明依赖于承诺方案，因此流程上与承诺方案类似，包含：

承诺：Prover生成承诺，并发送给Verifier
挑战：Verifier生成挑战数，并发送给Prover
打开/响应：Prover揭示明文或者证明，并发送给Verifier
验证：Verifier验证Prover提供的证明是否正确

Bulletproof关键流程如下：

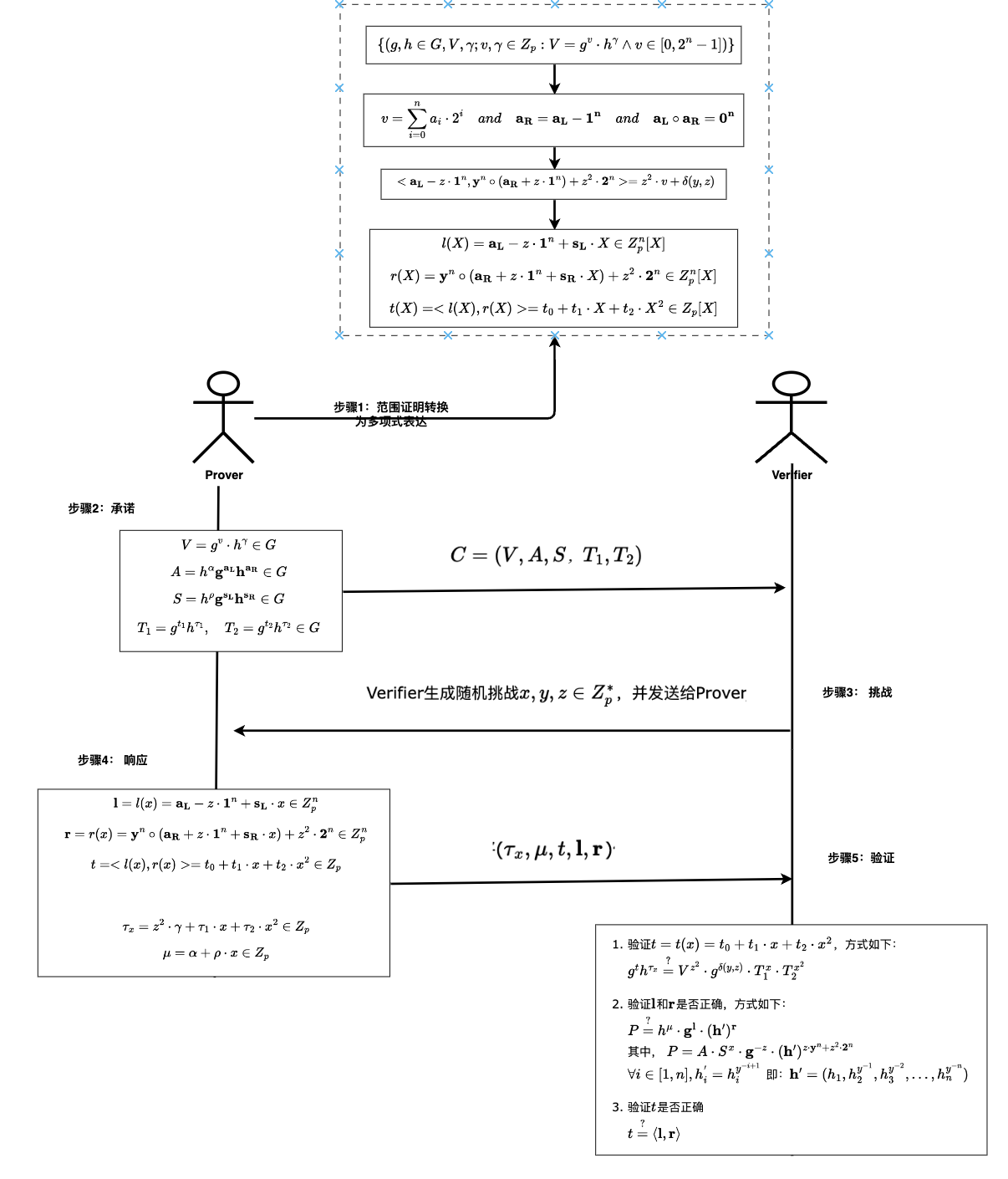
步骤1：范围证明转换为多项式表达，转换过程包含：形式化表示、向量内积表示、多项式表达等
步骤2：承诺
步骤3：挑战
步骤4：响应
步骤5：验证

下面我们针对每个步骤进行详细介绍。

范围证明形式化表示

下面我们以证明$v \in [0, 2^n - 1]$为例，介绍Bulletproof范围证明的构造和验证流程。首先，我们先对范围证明问题进行形式化表示。为了方便描述范围证明问题，我们将范围证明问题形式化表示如下：

\[\{ (g, h \in G, V, \gamma; v, \gamma \in Z_p : V = g^v \cdot h^\gamma \land v \in [0, 2^n - 1]) \} \]

其中，$g$和$h$是$G$生成元，$V$是$v$的Pedersen承诺，$\gamma$是随机数，$v$是需要证明的数值。从上述公式可以看出：

范围证明问题被转换成了两个部分：$v$的Pedersen承诺和$v$的范围大小
$v$的Pedersen承诺：$V = g^v \cdot h^\gamma$，与标准的Pedersen承诺形式一致
$v$的范围大小：$v \in [0, 2^n - 1]$，保证了$v$的值在一个合理的范围内。其中n是一个固定的数值，通常为64。

同时为了更方便的进行范围证明构造，Bulletproof会将范围证明问题转换为以下等式：

\[\begin{equation} v = \sum_{i=0}^{n} a_i \cdot 2^i \quad and \quad \mathbf{a_R} = \mathbf{a_L} - \mathbf{1^n} \quad and \quad \mathbf{a_L} \circ \mathbf{a_R} = \mathbf{0^n} \end{equation} \]

分析以上以上几个等式，可以很容易得出结论：

结论1：等式$v = \sum_{i=0}^{n} a_i \cdot 2^i$实际上是$v$的二进制表达
结论2：等式$\mathbf{a_R} = \mathbf{a_L} - \mathbf{1^n}$和等式$\mathbf{a_L} \circ \mathbf{a_R} = \mathbf{0^n}$限制了$\mathbf{a_L}$中元素$a_i$的取值范围必须为$0$或$1$

由于$\mathbf{a_L} \circ \mathbf{a_R} = \mathbf{a_L} \circ (\mathbf{a_L} - \mathbf{1^n}) = \mathbf{0^n}$，因此$\forall i \in [0, n], \quad a_i \cdot (a_i - 1) = 0$, 即$a_i$的值为0或1，因此结论2成立。

向量内积表示

Bulletproof范围证明会将等式$(1)$转换为向量内积形式，并将多个向量内积证明转换为一个向量内积证明问题。具体转换过程如下：

将等式$(1)$转换为向量内积形式

\[\begin{equation} v = \langle \mathbf{a_L}, \mathbf{2}^n \rangle \quad and \quad \langle \mathbf{a_L} - \mathbf{1}^n - \mathbf{a_R}, \mathbf{y}^n \rangle = 0 \quad and \quad \langle \mathbf{a_L}, \mathbf{a_R} \circ \mathbf{y}^n \rangle = 0 \end{equation} \]

其中，$\mathbf{y} = (y^0, y^1, y^2, ..., y^{n-1})$是长度为$n$的向量，$y$是一个随机数。由于$\mathbf{0}$向量与任意向量的内积为0，显然以上等式与$(1)$等价。

将多个向量内积证明转换为一个向量内积证明问题

通过引入另一个随机数$z$，我们可以将等式$(2)$合并为：

\[z^2 \cdot \langle \mathbf{a_L}, \mathbf{2}^n \rangle + z \cdot \langle \mathbf{a_L} - \mathbf{1}^n - \mathbf{a_R}, \mathbf{y}^n \rangle + \langle \mathbf{a_L}, \mathbf{a_R} \circ \mathbf{y}^n \rangle = z^2 \cdot v \]

为了方便后面范围证明的构造和验证，我们将上述等式展开为：

\[\begin{equation} \langle \mathbf{a_L} - z \cdot \mathbf{1}^n, \mathbf{y}^n \circ (\mathbf{a_R} + z \cdot \mathbf{1}^n) + z^2 \cdot \mathbf{2}^n \rangle = z^2 \cdot v + \delta(y, z) \end{equation} \]

其中，$\delta(y, z) = (z - z^2) \cdot \langle \mathbf{1}^n, \mathbf{y}^n \rangle - z^3\langle \mathbf{1}^n, \mathbf{2}^n \rangle \in Z_p$，从上面等式上我们可以了解到：

展开后的等式左边为向量内积形式
等式右边为常量，通过$(z, y, v)$进行计算，计算过程不涉及$\mathbf{a_L}$和$\mathbf{a_R}$。

范围证明多项式表达

我们知道在零知识证明中，一般将证明问题转换为多项式形式，然后Prover的多项式的承诺可以通过Verifier在随机打开点上验证完成。在Bulletproof中，Prover会将等式$(3)$转换为多项式形式，并由Verifier验证多项式的承诺是否正确。
首先我们定义两个线性向量多项式$l(X), r(X) \in Z_p^n[X]$, 和一个二次多项式$t(X) \in Z_p[X]$, 并定义如下：

\[l(X) = \mathbf{a_L} - z \cdot \mathbf{1}^n + \mathbf{s_L} \cdot X \in Z_p^n[X] \]

\[r(X) = \mathbf{y}^n \circ (\mathbf{a_R} + z \cdot \mathbf{1}^n + \mathbf{s_R} \cdot X) + z^2 \cdot \mathbf{2}^n \in Z_p^n[X] \]

\[t(X) = \langle l(X), r(X) \rangle = t_0 + t_1 \cdot X + t_2 \cdot X^2 \in Z_p[X] \]

其中，$\mathbf{s_L}$和$\mathbf{s_R}$是长度为$n$的随机向量，$t_0, t_1, t_2 \in Z_p$

通过上述定义，我们可以将等式$(3)$转换为多项式$t(X)$的形式, 其中常数项$t_0$等于$z^2 \cdot v + \delta(y, z)$, 即等式$(3)$右边部分。通过对多项式$t(X)$的承诺-挑战-打开-验证，我们可以间接证明等式$(3)$的正确性，即完成了对$v \in [0, 2^n - 1]$的范围证明。

Bulletproof交互式范围证明

承诺

Bulletproof首先会对关键参数$(\mathbf{a_L}, \mathbf{a_R})$进行承诺。步骤如下：

计算承诺
生成随机数$\alpha, \rho, \tau_1, \tau_2 \in z_p$和随机向量$\mathbf{s_L}$, $\mathbf{s_R} \in z_p^n$, 并计算承诺$C = (V, A, S， T_1, T_2)$

\[V = g^v \cdot h^{\gamma} \in G \]

\[A = h^{\alpha}{\mathbf{g}}^{\mathbf{a_L}}{\mathbf{h}}^{\mathbf{a_R}} \in G \]

\[S = h^{\rho}{\mathbf{g}}^{\mathbf{s_L}}{\mathbf{h}}^{\mathbf{s_R}} \in G \]

\[T_1 = g^{t_1}h^{\tau_1}, \quad T_2 = g^{t_2}h^{\tau_2} \in G \]

需要说明的是：

$\mathbf{a_L}$和$\mathbf{a_R}$与等式$(2)$中的对应。
$A$是$\mathbf{a_L}$和$\mathbf{a_R}$的Pedersen承诺
$S$是$\mathbf{s_L}$和$\mathbf{s_R}$的Pedersen承诺, 用于隐藏范围证明多项式表达中使用的$\mathbf{a_L}$和$\mathbf{a_R}$的值（注: $\mathbf{a_L}$和$\mathbf{a_R}$与$v$强绑定，因此需要隐藏）
$T_1$和$T_2$是对多项式$t(X)$的系数承诺

Prover将承诺$C$发送给Verifier

挑战

Verifier生成随机挑战$x, y, z \in Z_p^*$，并发送给Prover, 其中：

$x$是对多项式承诺的挑战
$y$用于生成公式$(2)$中的$\mathbf{y}$，是对$v$范围的挑战
$z$对应公式$(3)$中的$z$，是对等式$(3)$的挑战

打开/响应

Prover根据接收到的挑战$y, z$，计算多项式$t(X)$的值，并将响应发送给Verifier

计算多项式点打开$l(x), r(x), t(x)$

\[\mathbf{l} = l(x) = \mathbf{a_L} - z \cdot \mathbf{1}^n + \mathbf{s_L} \cdot x \in Z_p^n \]

\[\mathbf{r} = r(x) = \mathbf{y}^n \circ (\mathbf{a_R} + z \cdot \mathbf{1}^n + \mathbf{s_R} \cdot x) + z^2 \cdot \mathbf{2}^n \in Z_p^n \]

\[t = \langle l(x), r(x) \rangle = t_0 + t_1 \cdot x + t_2 \cdot x^2 \in Z_p \]

计算随机响应$\tau_x, \mu$

\[\tau_x = z^2 \cdot \gamma + \tau_1 \cdot x + \tau_2 \cdot x^2 \in Z_p \]

\[\mu = \alpha + \rho \cdot x \in Z_p \]

注：Prover在打开阶段时，计算的响应用到了承诺阶段的一些随机数和随机向量，如$\alpha, \rho, \tau_1, \tau_2, \mathbf{s_L}, \mathbf{s_R}$等。

Prover将($\tau_x, \mu, t, \mathbf{l}, \mathbf{r}$)作为响应发送给Verifier

验证

Verifier接收到Prover的响应后，验证Prover提供的证明是否正确。Verifier需要验证多个等式是否成立：

验证$t = t(x) = t_0 + t_1 \cdot x + t_2 \cdot x^2$，方式如下：
$g^th^{\tau_x} \stackrel{?}{=} V^{z^2} \cdot g^{\delta(y, z)} \cdot T_1^x \cdot T_2^{x^2}$
验证$\mathbf{l}$和$\mathbf{r}$是否正确，方式如下：
$ P \stackrel{?}{=} h^{\mu} \cdot \mathbf{g}^{\mathbf{l}} \cdot (\mathbf{h'})^{\mathbf{r}}$
其中， $P = A \cdot S^x \cdot \mathbf{g}^{-z} \cdot (\mathbf{h'})^{z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n}$
$\forall i \in [1, n], h_i^{'} = h_i^{y^{-i+1}}$ 即：$\mathbf{h'} = (h_1, h_2^{y^{-1}}, h_3^{y^{-2}}, ..., h_n^{y^{-n}})$
验证$t$是否正确
$t \stackrel{?}{=} \langle \mathbf{l}, \mathbf{r} \rangle$

如果上述等式都成立，则Verifier接受Prover的范围证明，即$v \in [0, 2^n - 1]$; 否则Verifier拒绝Prover的证明。

正确性验证

验证$t = t(x) = t_0 + t_1 \cdot x + t_2 \cdot x^2$

\[V^{z^2} \cdot g^{\delta(y, z)} \cdot T_1^x \cdot T_2^{x^2} \]

\[= (g^v \cdot h^{\gamma})^{z^2} \cdot g^{\delta(y, z)} \cdot (g^{t_1}h^{\tau_1})^x \cdot (g^{t_2}h^{\tau_2})^{x^2} \]

\[= g^{v \cdot z^2} \cdot h^{\gamma \cdot z^2} \cdot g^{\delta(y, z)} \cdot g^{t_1 \cdot x} \cdot h^{\tau_1 \cdot x} \cdot g^{t_2 \cdot x^2} \cdot h^{\tau_2 \cdot x^2} \]

\[= g^{v \cdot z^2 + \delta(y, z) + t_1 \cdot x + t_2 \cdot x^2} \cdot h^{\gamma \cdot z^2 + \tau_1 \cdot x + \tau_2 \cdot x^2} \]

\[= g^{t_0 + t_1 \cdot x + t_2 \cdot x^2} \cdot h^{z^2 \cdot \gamma + \tau_1 \cdot x + \tau_2 \cdot x^2} \]

\[= g^t \cdot h^{\tau_x} \]

因此，$g^th^{\tau_x} = V^{z^2} \cdot g^{\delta(y, z)} \cdot T_1^x \cdot T_2^{x^2}$成立,同时从上述推导中我们可以看到主要是验证了$t=t(x)$的正确性。

验证$\mathbf{l}$和$\mathbf{r}$是否正确

\[P = A \cdot S^x \cdot \mathbf{g}^{-z} \cdot (\mathbf{h'})^{z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n} \]

\[= h^{\alpha}{\mathbf{g}}^{\mathbf{a_L}}{\mathbf{h}}^{\mathbf{a_R}} \cdot (h^{\rho}{\mathbf{g}}^{\mathbf{s_L}}{\mathbf{h}}^{\mathbf{s_R}})^x \cdot \mathbf{g}^{-z} \cdot (\mathbf{h'})^{z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n} \]

\[= h^{\alpha}{\mathbf{g}}^{\mathbf{a_L}}{\mathbf{h}}^{\mathbf{a_R}} \cdot h^{\rho \cdot x}{\mathbf{g}}^{\mathbf{s_L} \cdot x}{\mathbf{h}}^{\mathbf{s_R} \cdot x} \cdot \mathbf{g}^{-z} \cdot (\mathbf{h'})^{z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n} \]

\[= h^{\alpha + \rho \cdot x}{\mathbf{g}}^{\mathbf{a_L} + \mathbf{s_L} \cdot x - z \cdot \mathbf{1}^n} \cdot {\mathbf{h}}^{\mathbf{a_R} + \mathbf{s_R} \cdot x} \cdot (\mathbf{h'})^{z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n} \]

\[= h^{\mu}{\mathbf{g}}^{\mathbf{l}} \cdot h^{\mathbf{a_R} + \mathbf{s_R} \cdot x} \cdot (\mathbf{h'})^{z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n} \]

根据$\mathbf{h'}$的定义，我们可以得到：

\[\mathbf{h'}^{\mathbf{y^n}} = (h_1^{y^0}, (h_2^{y^{-1}})^{y^1}, (h_3^{y^{-2}})^{y^2}, ..., (h_n^{y^{-n+1}})^{y^{n-1}}) \]

\[= (h_1, h_2, h_3, ..., h_n) = \mathbf{h} \]

因此$P$可以简化为：

\[P = h^{\mu}{\mathbf{g}}^{\mathbf{l}} \cdot h^{\mathbf{a_R} + \mathbf{s_R} \cdot x} \cdot (\mathbf{h'})^{z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n} \\ \]

\[= h^{\mu} \cdot \mathbf{g}^{\mathbf{l}} \cdot (\mathbf{h'})^{\mathbf{y}^n \circ (\mathbf{a_R} + \mathbf{s_R} \cdot x) + z \cdot \mathbf{y}^n + z^2 \cdot \mathbf{2}^n} \]

\[= h^{\mu} \cdot \mathbf{g}^{\mathbf{l}} \cdot (\mathbf{h'})^{\mathbf{y}^n \circ (\mathbf{a_R} + z \cdot \mathbf{1}^n + \mathbf{s_R} \cdot x) + z^2 \cdot \mathbf{2}^n} \\ \]

\[= h^{\mu} \cdot \mathbf{g}^{\mathbf{l}} \cdot (\mathbf{h'})^{\mathbf{r}} \]

因此, $P = h^{\mu} \cdot \mathbf{g}^{\mathbf{l}} \cdot (\mathbf{h'})^{\mathbf{r}}$成立，从上面公式我们可以看到主要是验证了$\mathbf{l}$和$\mathbf{r}$的正确性。

验证$t$是否正确

t的正确性验证比较简单，由于Prover在打开阶段计算的$t$是多项式$l(x)$和$r(x)$的内积，因此只需要Verifier重新计算$l(x)$和$r(x)$的内积，然后与Prover提供的$t$进行比较即可。如果相等，则说明Prover提供的$t$是正确的。

结语

本文作为Bulletproof范围证明系列文章的第一篇，详细介绍了Bulletproof范围证明的多项式表达、承诺、挑战、打开、验证等流程。Bulletproof范围证明是一种零知识证明技术，主要用于证明某个值在一个合理的范围内。Bulletproof范围证明具有高效性、透明设置、可聚合性等特点，因此在实际应用中得到了广泛的应用。

本文未对Bulletproof范围证明的优化、聚合、批量验证等技术进行详细介绍，后续文章会逐步展开对Bulletproof的进一步介绍，展示Bulletproof备受欢迎的魅力所在。

posted @ 2024-11-01 20:26 warm3snow 阅读(15) 评论(0) 编辑收藏举报

刷新页面返回顶部

warm3snow