门罗币隐私保护之环签名
主页
微信公众号:密码应用技术实战
博客园首页:https://www.cnblogs.com/informatics/
GIT地址:https://github.com/warm3snow
简介
在《门罗币隐私保护之隐形地址》文章中,我们重点介绍了门罗币Monero的隐形地址技术,门罗币通过隐形地址保证了交易的不可链接性,并实现了用户的隐私保护和监管需求。
本文将继续介绍门罗币的另一个核心技术——环签名技术,Monero通过环签名技术,实现了交易的不可追踪性。
- 不可链接性(Unlinkability):对于任何两笔outgoing交易,无法证明它们是发送给同一个人的。即对于任何两个 outgoing 交易,无法证明它们是由同一个人收款的。
- 不可追踪性(Untraceability):对于每一笔incoming交易,所有可能的发送者都是等概率的。这意味着,对于任何两个incoming交易,无法证明它们是由同一个人发送的。
注:incoming和outgoing交易分别表示用户的收款和支出交易。
基础知识
术语定义
- \(\mathbb{Z}_l\):有限域,\(l\)是一个大素数,如:\(l = 2^{252} + 27742317777372353535851937790883648493\)
- \(S\):环签名的环,一组公钥的集合,\(S = {P_1, P_2, ..., P_n}\),包含\(P_s\)
- \(P_i\):公钥,在环签名中表示环中第\(i\)个公钥, 当\(i = s\)时,\(P_s\)是签名者的公钥
- \((x_s, P_s)\):用户公私钥对, 公钥为\(P_s\), 私钥为\(x_s\)且$ x_s \in \mathbb{Z}_l$
- \(\sigma\):环签名的签名结果
- \(m\):待签名的消息。在签名时,通常会先对消息进行哈希处理。
- \(H_s\):密码学哈希函数, 将输入映射到\(\mathbb{Z}_l\),如:\(H_s: \{0, 1\}^* \rightarrow \mathbb{Z}_l\)
- \(H_p\):密码学哈希函数, 将输入映射到椭圆曲线上的点,如:\(H_p: \{0, 1\}^* \rightarrow E(\mathbb{F}_q)\)
- \(I\):密钥镜像,在门罗币中使用,用于防止双花攻击
环签名
环签名(Ring Signature)是一种数字签名方案,允许一组用户中的任何一个用户为某个消息生成签名,而不需要透露具体是哪个用户生成的签名。环签名的主要特点是它提供了签名的匿名性和可验证性,确保签名者的身份在签名过程中保持隐私。
环签名的基本概念
- 环:环签名的“环”指的是一组公钥,这些公钥代表了可能的签名者。签名者在生成签名时,会选择一个环中的公钥作为自己的身份,但外部观察者无法确定具体是哪个公钥对应的用户。
- 签名:签名者使用自己的私钥和环中其他用户的公钥生成签名。这个签名可以被任何人验证,但无法确定签名者的身份。
- 验证:任何人都可以使用环来验证签名的有效性,确保签名确实是由环中的某个用户生成的。
环的大小是环签名方案的一个重要参数,环越大,签名者的身份越难以确定,签名的匿名性越高。但是环的大小也会影响签名的计算和验证性能,因此需要在匿名性和性能之间进行权衡。
环签名构造和验证流程
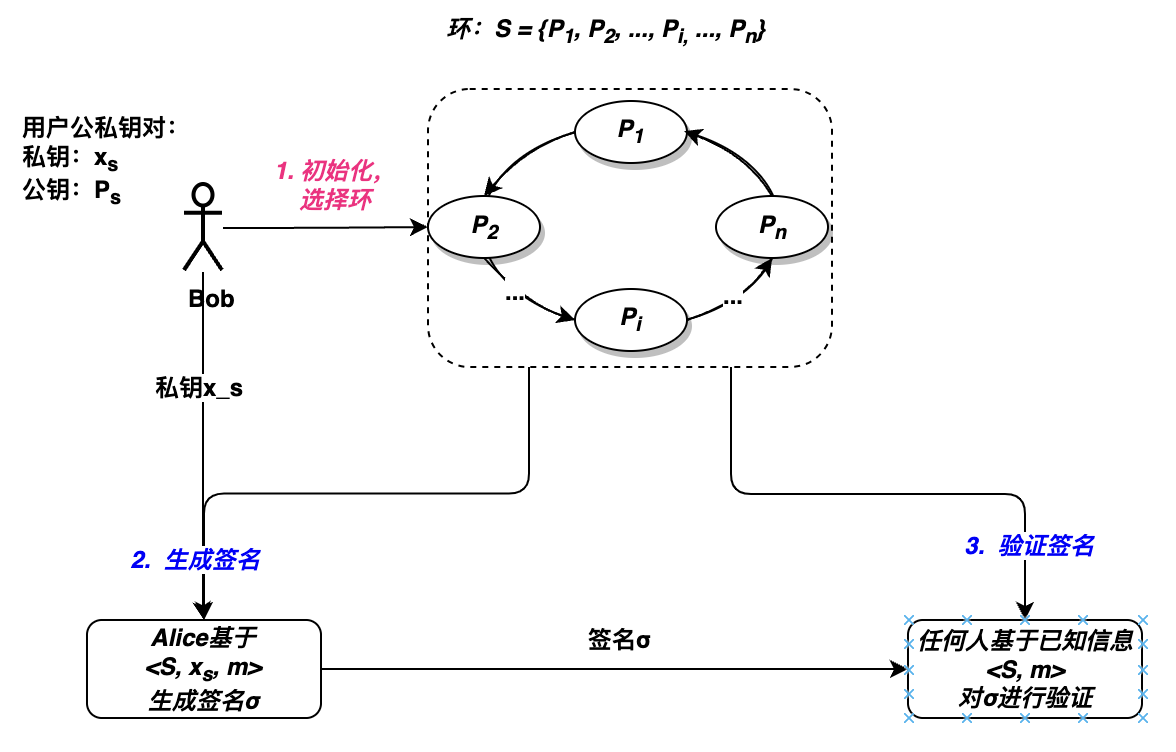
- 初始化:签名者Bob选择环S中的公钥,如{\({P_1, P_2, ..., P_i, ..., P_n}\)},其中Bob自身的公钥\(P_s\)也在放入环S中
- 生成签名:Bob基于环S中的公钥和自己的私钥\(x_s\)以及待签名消息\(m\),生成环签名\(\sigma\)
- 验证签名:任何人都可以基于环S,消息m对签名\(\sigma\)进行验证
环签名方案涉及一个三元组\((KeyGen, Sign, Verify)\),其中:
- \(KeyGen\):密钥生成算法,签名者使用\(KeyGen\)生成公私钥对\((x_s, P_s)\)
- \(Sign(m, S, x_s)\):签名算法,签名者使用\(Sign\)生成环签名\(\sigma\), 其中\(m\)是消息,\(S\)是环,\(x_s\)是签名者的私钥
- \(Verify(m, S, \sigma)\):验证算法,任何人都可以使用\(Verify\)验证签名的有效性。算法结果为布尔值,\(true\)表示签名有效,\(false\)表示签名无效。
门罗币之环签名
回顾在《门罗币隐私保护之隐形地址》介绍的交易模型,Bob作为收款方,能够验证每一笔相关交易的有效性。
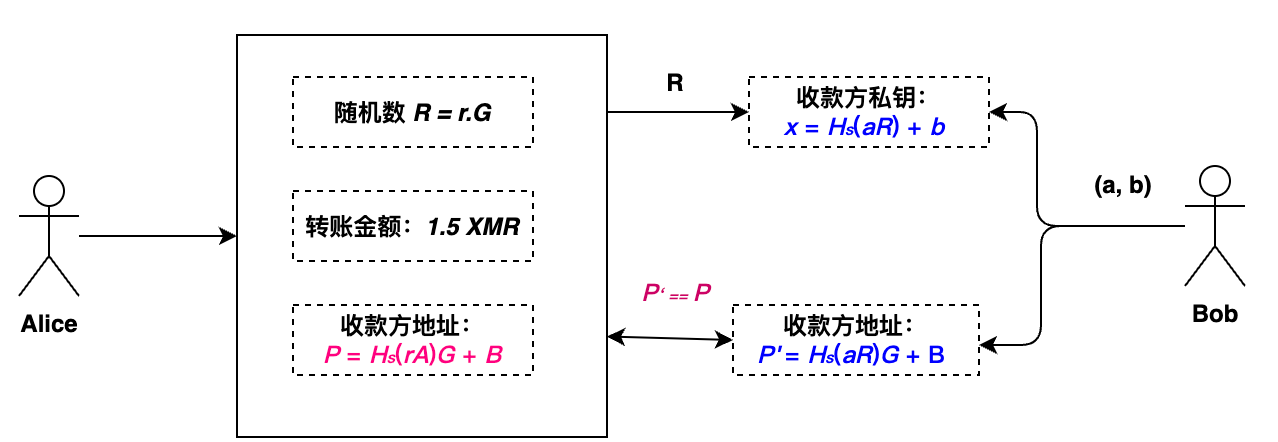
进一步说明:
- Bob作为收款人,在验证每笔交易时,Bob只需对每个输出执行两次椭圆曲线乘法和一次加法(即生成\(P'\)),以检查该交易是否属于他。
- 对于每个属于Bob的UTXO,Bob恢复一个密钥对\((x, P)\)并将其存储在钱包中。
- 只有Bob可以生成地址\(P\)的私钥\(x\),因此只有Bob能够花费这笔收入。
值得注意的是,\((x, P)\)是一次性密钥,当Bob花费这笔收入时,会使用该密钥参与环签名,之后可以丢弃。
门罗币环签名
门罗币使用环签名技术,实现了交易的不可追踪性。门罗币的环签名方案基于CryptoNote协议。在CryptoNode协议中,环签名交易模型如下:
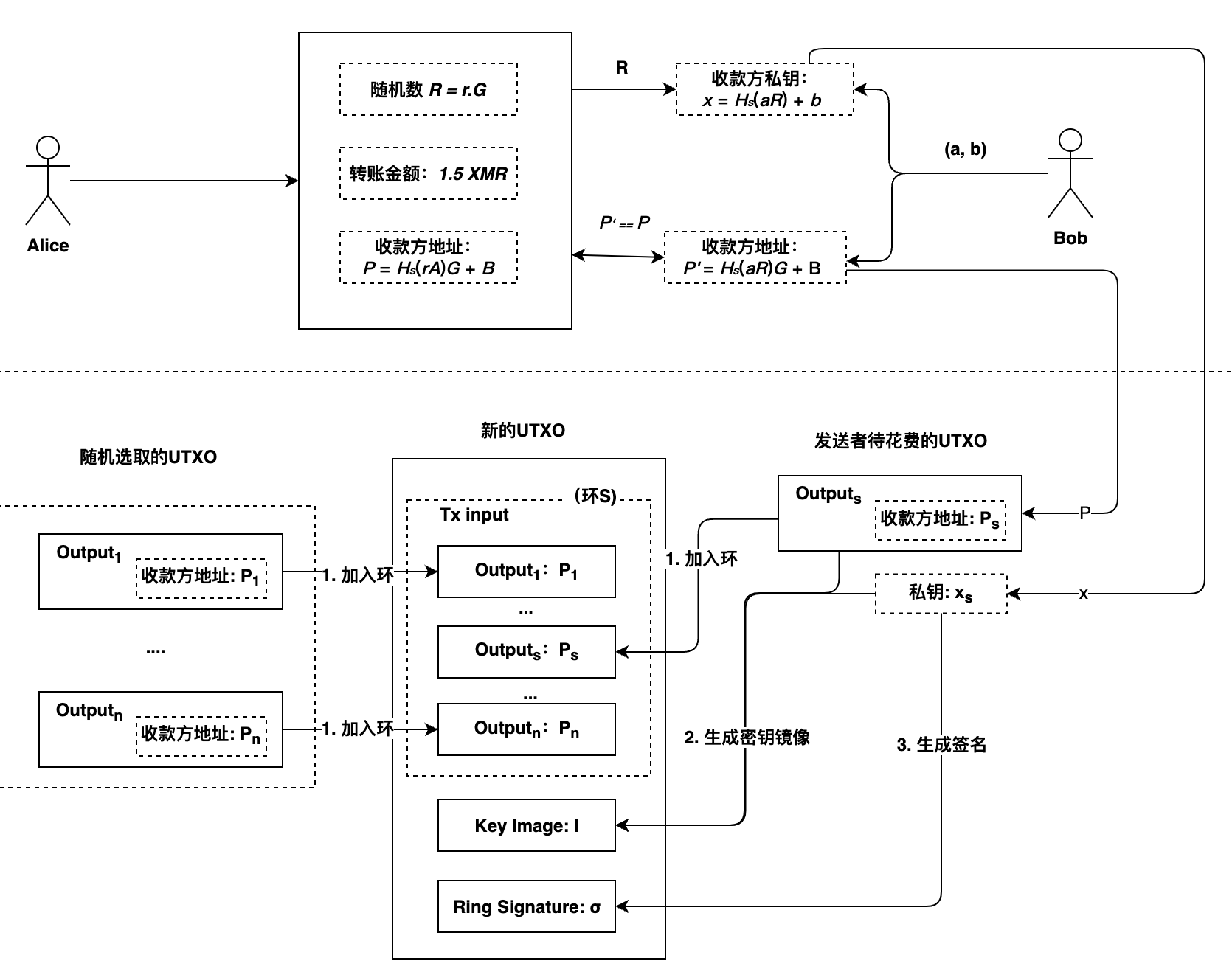
- 加入环:Bob从门罗币公开账本中随机选择UTXO,以及自己待花费的UTXO,放入到新创建的UTXO中,作为交易的Tx input, 所有UTXO的收款方地址{\({P_1, ..., P_s, ..., P_n}\)}构成环\(S\)
- 生成密钥镜像:Bob使用自己的签名私钥\(x_s\)和公钥\(P_s\), 生成密钥镜像\(I\),区块链矿工在验证交易时,会验证\(I\)是否已经被使用过,以防止双花攻击
- 生成签名:Bob使用环\(S\)和自己的私钥\(x_s\),对交易进行签名,生成环签名\(\sigma\)
门罗币环签名方案
门罗币环签名方案涉及一个四元组\((KeyGen, Sign, Verify, Link)\),其中:
- \(KeyGen, Sign, Verify\)与一般的环签名方案功能类似
- \(Link\):区块链矿工通过\(Link\)算法验证对应的密钥镜像\(I\)是否已经被使用过,以防止双花攻击
密钥生成KeyGen
门罗币的KeyGen算法与一般的环签名方案类似,目的都是生成公私钥对\((x_s, P_s)\),其中\(P_s\)是签名者的公钥,\(x_s\)是签名者的私钥。
不同的是:
- 门罗币的公私钥来自于隐形地址技术,即\(P_s = H_s(aR)G + B\), 对应的私钥\(x_s = H_s(aR) + b\)
- 门罗币的KeyGen算法还会生成密钥镜像\(I\),与公私钥一一对应。其中, \(I = x_s \cdot H_p(P_s)\)
签名算法Sign
在门罗币中,由于签名公私钥对\((x_s, P_s)\)是由隐形地址技术生成的,并且仅用于一次性签名,因此门罗币环签名我们也称为一次性环签名。
门罗币的Sign算法如下:
- 初始化:
- 随机选取其他用户的公钥\(P_i\),并合并自己的公钥\(P_s\),构成环\(S\), 如:\(\{ {P_1, P_s, ..., P_i, ..., P_n}\}\)
- 选择两个随机数集合\(Q\)和\(W\),如下
- \(Q = \{q_i\}\) , \(i = 1, 2, ..., n \quad q_i \in \mathbb{Z}_l\)
- \(W = \{w_i\}\) , \(i = 1, 2, ..., n \quad i \neq s \quad w_i \in \mathbb{Z}_l\)
- 计算环签名
环签名的签名算法,类似零知识承诺,包含:承诺-挑战-响应等几个步骤
- 计算承诺,承诺由两个集合组成\(L\)和\(R\),集合元素计算分别如下:
- 计算挑战(实际上是前面已有知识的哈希值)
其中,\(m\)是待签名的消息,在这里表示交易信息(签名除外,因为签名还未生成)
- 计算响应
输出签名\(\sigma\), 如下:
验证算法Verify
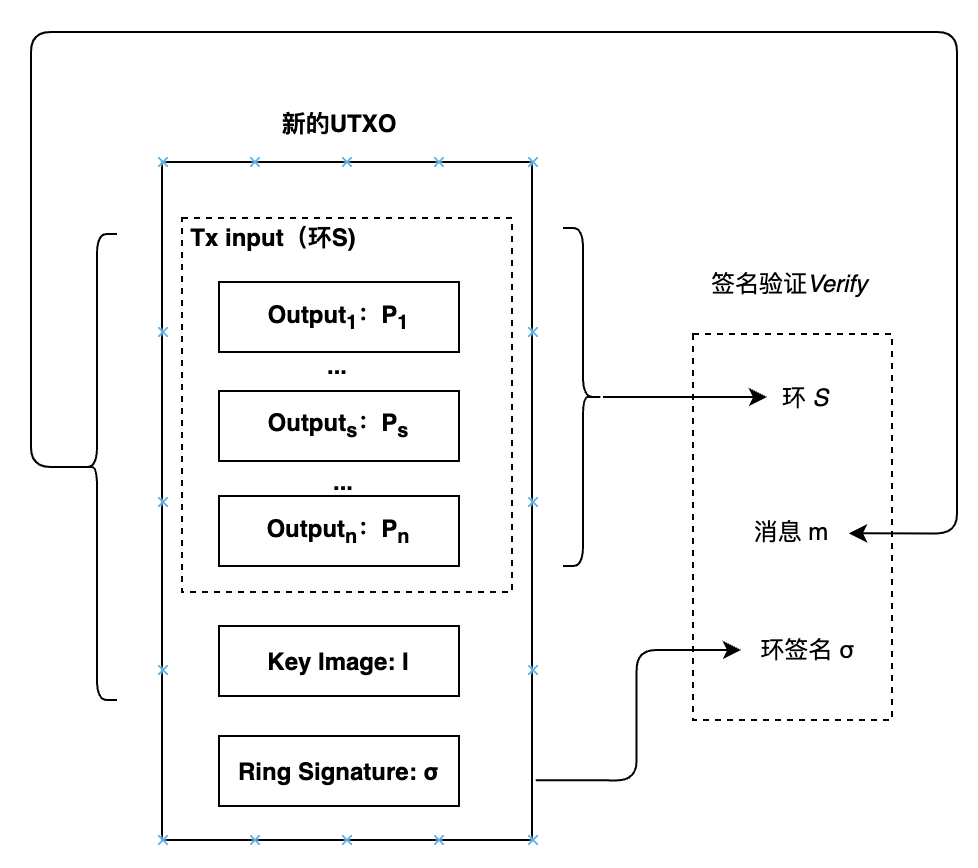
区块链矿工在收到交易后,会对交易进行签名验证。矿工已知环\(S = {P_1, P_2, ..., P_n}\),以及环签名\(\sigma = (I, c_1, ..., c_n, r_1, ..., r_n)\), 签名验证Verify算法如下:
- \(L^{'}\)和\(R^{'}\)为两个集合,\(\forall i \in [0, n]\)
- 签名验证等式
如果上述等式成立,则签名有效,否则签名无效,交易被拒绝。
正确性验证
- 计算\(L^{'}\)
在上述推导中,由于\(P_s = x_s \cdot G\),所以:\(-c_s \cdot x_s \cdot G + c_s \cdot P_s = -c_s \cdot P_s + c_s \cdot P_s = 0\)
- 计算\(R^{'}\)
在上述推导中,由于\(I = x_s \cdot H_p(P_s)\),所以:\(-c_s \cdot x_s \cdot H_p(P_s) + c_s \cdot I = -c_s \cdot I + c_s \cdot I = 0\)
- 计算\(\sum_{i=0}^{n} c_i\)
由于\(L^{'} = L\)且\(R^{'} = R\),所以:
因此,签名验证等式成立,签名有效。
双花验证Link
已知密钥镜像\(I\)和用户密钥\((x_s, P_s)\)的计算关系如下:
根据密钥镜像\(I\)的计算方式,我们可以知道用户密钥和密钥镜像之间存在一一对应关系,而用户密钥\((x_s, P_s)\)基于隐形地址技术,只使用一次,且与交易绑定。
矿工会记录所有交易的密钥镜像列表,在收到新交易时,会检查交易中的\(I\)是否已存在于列表中,如果存在,则说明该交易对应的\((x_s, P_s)\)已经被使用过,是一笔双花交易,交易被拒绝。
结语
环签名是门罗币的另一个核心技术,通过环签名技术,实现了交易的不可追踪性。本文简单介绍了环签名的基本概念,并详细介绍了门罗币的环签名方案,包括密钥生成、签名、验证和双花验证等算法。希望通过本文的介绍,读者对隐私币的匿名技术有更进一步的了解。
门罗币隐私保护使用了多种技术,包括隐形地址、环签名、机密交易等,这些技术共同构成了门罗币的隐私保护体系。在接下来的文章中,我们将继续介绍门罗币的其他隐私保护技术。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号